多重化    Multiplexing

 与えられた周波数帯域を多数の人が混信しないで通信することを多元接続 (Multiple Access) と呼んでいます。　いろんな方法があって、しかもそれらの組み合わせを用いているので、方式は数えられないぐらいあります。　実際、通信システムそれぞれが固有の多元接続を特徴としていますので、十人十色といった有様です。　それらをどう分類するか難しいのですが、とりあえず、このページではオーソドックスな周波数分割多重と時分割多重と符号分割多重の３つについて説明します。　これらは、物理的にチャンネルを確保する方法です。　この分類を回線接続型多元接続と呼ぶことにしましょう。　
これに対して、非回線接続型多元接続は、物理的な接続が常時確保されないという方式があります。　アクセス方法は、キャリヤ・センス（他人が通信しているかどうかの判定）をして、誰も使用していないならば、相手の番号を付けたデータフレームを送るというランダムアクセスです。その典型は無線ＬＡＮなどです。

多重化 (Multiplex ) という言葉は古くから使われていますが、親と子が定められた環境で、上り回線（または下り回線）を、たくさんの子が一斉に通信する方法を指します。　あまりにも多くの方式があるために、最近は用語が混乱しているようです。　非回線接続型を含め、総括的な多元接続については、実際の通信システムの例を見ながら、ページを改めて解説するつもりです。

さらに、Celluler などでは、空間的な分割も大きな要素になっています。一つは、スマートアンテナなどによって移動端末に電波の指向性を追随させることによる多重化、　二つは、MIMO (Multiple Input Multiple Output、ブラインド問題を参照) のように、同一周波数帯域内で、電波の干渉を逆手にとって利用しようとする多重化、　三つは、セル間干渉を避ける意味での多重化です。これらは、それぞれ固有の問題をはらんでおり、内容的にもボリュームが大きいので、個別に解説することにします。

付け足しですが、２重化 (Duplex ) という用語も広く用いられています。　これは、対向する送信者と受信者が双方向で通信するときの方式を指しています。　たとえば、TDD (Time Division Duplex) は周波数帯域（WHz）を使って時間的に交互に上りと下りの通信を行う方式を言い、FDD (Frequency Division Duplex) はWHz の帯域を半分に分割して上り専用と下り専用に分けて同時に通信する方式を言います。　

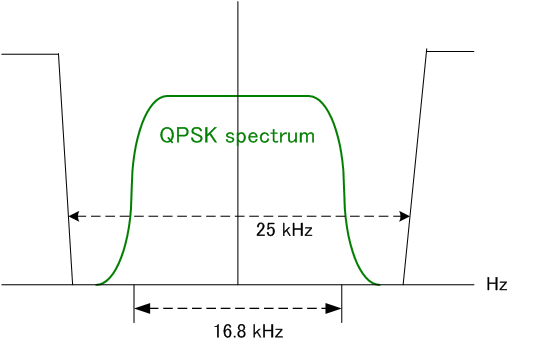
Ａ：　周波数分割多重（ ＦＤＭ：Frequency Division Multiplex )
現行のラジオやテレビなどのアナログ放送がＦＤＭ の代表的なものです。　これらのアナログ放送では、広い周波数帯域を分割して各放送局に配給しています。　受信機は聞きたいチャンネルの周波数を選択します。　ディジタル通信でもやはり、まずは周波数帯域が配給されます。　ただし、ディジタル通信では配給された周波数帯域を独りの人が占有することはあまりなく、この帯域を更に後述の ＴＤＭ や ＣＤＭ で多重化します。　周波数帯域が配給されるという意味は、その帯域の外へ信号エネルギーを漏らしてはいけませんということを意味しています。　第２世代の Full Rate PDC では１６MHzの帯域幅を６４０チャンネルに周波数分割しています。１チャンネル当りの周波数幅は２５ｋHzになります。　実際の信号はこの周波数幅を少し余裕もって通過しなくてはなりませんが、その様子を下図に示します。

 img11.gif

上の図では、信号スペクトルが半値幅１６．８KHzの余弦ロールオフで描かれています。　このようなスペクトルをもつパルスを用いて、ＱＰＳＫ（４値ＱＡＭ）という変調方式で３３．６ｋｂｐｓの情報伝送速度を実現しています。　ＰＤＣでは、ＦＤＭされたチャンネルをさらに３人で（ハーフレートでは６人で）ＴＤＭしています。　単純に３３．６ｋｂｐｓを３人で割ると１１．２ｋｂｐｓ/人　となりますが、これは１台のＰＤＣから発信されるディジタル情報の平均速度を表しています。　瞬間的には、この３倍速の３３．６ｋｂｐｓで送信されているので間違わないようにしてください。　とくに、この瞬間速度（３３．６ｋｂｐｓ）のことをベアラーレート（Bearer ＝運搬人）と呼んでいます。　１６．８ｋｂｐｓ/人の内訳は、ＴＤＭ のフレーム間余裕＋通信用プロトコル＋誤り訂正＋実質的なディジタル音声、となっており、実質のディジタル音声の速さはこれよりも遅くなります。　６４ｋｂｐｓのＩＳＤＮで電話する場合に比べて1/５以下の圧縮になっています。
FDM の概念を整理すると次のようです。　時間幅 秒、周波数幅 の複素信号を使って、人の送信者を多重化する方法を分類してみます。　この複素信号の自由度は です。　自由度 の複素信号は時間軸のサンプル値列

または、周波数軸のサンプル値列

のどちらか一方で完全に表現されます。　自由度 をすべて時間軸に配分してしまうと、パルス時間幅が  秒になり、それぞれのパルスは の帯域をいっぱいに使ってしまいます。　逆に、自由度 をすべて周波数軸に配分すると、一つの自由度を送るのに時間幅 秒のパルスが必要になります。　自由度が８の場合を例とし、８人の送信者に平等に自由度を一個づつ配分するとします。　そして、送信者は一つの自由度を用いて一つのシンボルを送るとします。　周波数分割多重（FDM）は送信者に周波数サンプル値 を割り付ける方法です。　図式的に表現すると下図のように描けます。　８本のバーは、８人の送信者が の周波数帯域を利用して、８時刻分をかけて一つのシンボルを送っていることを表しています。　もし、多重化しなければ（一人の送信者が の帯域を独占すれば）、送信者は８時刻で８つのシンボルを送ることができるわけです。　一般に、使用する周波数帯域とパルスの送信間隔との間に反比例の関係があります（周波数分析参照）。

img21.gif

Ｂ：　時分割多重 (TDM: Time Division Multiplex )
高速のベアラーレートで通信しているときのビット列は下図のようなフレーム構造をもっています。

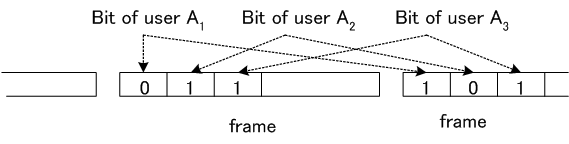
img6.gif

このフレームの第１ビットは送信者 の情報、第２ビットは送信者 の情報、といった具合に多重化するのがビット多重です。　ＰＤＣでは、下図のように長いフレームを280ビットの３つのスロットに分け、３人で時分割多重しています。　このような方式をスロット多重と呼んでいます。

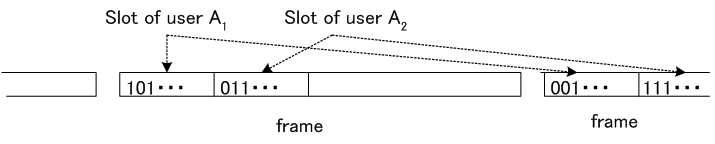
img10.gif

ＰＤＣでは、ＦＤＭをしたあとで、更にスロットで時分割多重しています。　上と同様な図式に従えば、TDM は下図のようになります。

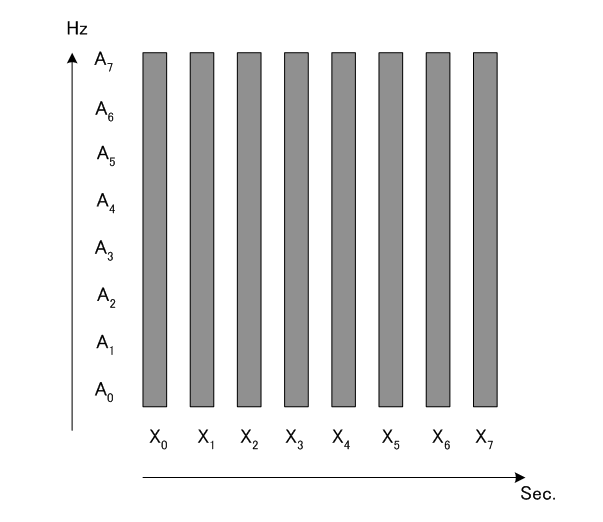
img22.gif

８人の送信者に対して１時刻づつ割り当て、周波数帯域をいっぱいに使って一つのシンボルを伝送しています。

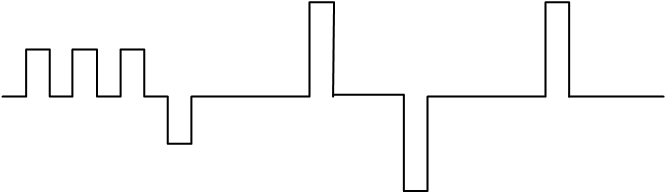
Ｃ：　符号分割多重 (CDM: Code Division Multiplex )
上のような線図を平面化したのがCDMA です。　TDM では、時刻毎に一つの自由度を一人の送信者に配分しましたが、その配分を時間軸に沿って1/8づつ薄く配分してみます。　すなわち、どの時刻も８人の送信者の情報が薄められて多重化されることになります。　送信者は８時刻を使って一つのシンボルを送ります。　受信者が多重化をほどくことができれば、このような方法も考えられます。　これがＣＤＭです。　仕掛けは、８時刻長の（８次元の）直交符号を８人に配分します。　受信信号は直交ベクトルの一次結合ですが、直交性の条件からユーザー別に分離して送信データを検出することができます。　この考えを周波数軸から考えてもまったく同じ結果を得ます。　すなわち、時間軸で設計した８つの直交ベクトルは、それらを離散フーリェ変換すればやはり周波数軸で直交しますから、これらを周波数軸のＣＤＭＡ 符号と考えればいいわけです。
具体的な例題で原理を説明します。　簡単のため、受信者を４人とします。各受信者には２値情報（＋１とー１）を送るものとします。　たとえば、送りたい情報を

Ａ１：　＋１、＋１、−１、＋１、・・・・
Ａ２：　＋１、−１、−１、＋１、・・・・
Ａ３：　−１、−１、＋１、−１、・・・・
Ａ４：　−１、−１、−１、＋１、・・・・

としましょう。　次に、４人の受信者に長さ４チップ（ＣＤＭＡでは chip と呼ぶ）の下のような２値ＣＤＭ 符号を割り当て、符号全体に送信データの＋１や−１を掛けて加算して送るようにします。　もう少し具体的に記述してみましょう。　４人に対して以下のようなＣＤＭ 符号を配給しておきます。　ｔ１、ｔ２、・・などはベクトル表示です。

Ａ１に　　（＋１、＋１、＋１、＋１）＝ｔ１
Ａ２に　　（＋１、＋１、−１、−１）＝ｔ２
Ａ３に　　（＋１、−１、−１、＋１）＝ｔ３
Ａ４に　　（−１、＋１、−１、＋１）＝ｔ4

この符号は、互いに直交するようになっています。　数学的にいえば、異なるベクトルどうしの内積（対応する要素の積の和）がゼロになることですが、具体的にチェックしてみると、たとえばＡ２君とＡ３君の内積は、

（＋１）＊（＋１）＋（＋１）＊（−１）＋（−１）＊（−１）＋（−１）＊（＋１）＝０

となり、たしかにゼロになっています。　４人への送信チップ列（パルス列）は下のようになります。　分かりやすくするために、４チップの区切りに／を入れてあります。

Ａ１：　/+1,+1,+1,+1/+1,+1,+1,+1/-1,-1,-1,-1,/+1,+1,+1,+1/.....
Ａ２：　/+1,+1,-1,-1/-1,-1,+1,+1/-1,-1,+1,+1/+1,+1,-1,-1/.....
Ａ３：　/-1,+1,+1,-1/-1,+1,+1,-1/+1,-1,-1,+1/-1,+1,+1,-1/.....
Ａ４：　/+1,-1,+1,-1/+1,-1,+1,-1/+1,-1,+1,-1/-1,+1,-1,+1/.....

このチップ列を単純に加算した系列

Ｙ：　　/+2,+2,+2,-2/ 0, 0, +4, 0/ 0,-4, 0, 0/ 0, +4, 0,,0/.....

を送信します。　実際のパルス列で描けば下のようなものです。

 img8.gif

このパルス列を受信した４人は、受信信号の区切り毎に、自分のＣＤＭ 符号との内積を計算します。　たとえば、Ａ３君は、自分の符号（＋１、−１、−１、＋１）と最初の４つの受信チップ列（＋２、＋２、＋２、−２）との内積、

（＋１）＊（＋２）＋（−１）＊（＋２）＋（−１）＊（＋２）＋（＋１）＊（−２）＝−４

を計算します。　この結果はＡ３君への最初のデータ（−１）と極性が一致しますね。　その理由は、自分の符号と、Ａ１君やＡ２君やＡ４君の符号との内積がゼロになることから来ています。
このような操作をベクトルで説明すると非常に簡単です。　Ａ１君へのデータをa1、Ａ２君へのデータをa2、・・・とすると、送信ベクトルは

y = a1t1 + a2t2 + a3t3 + a4t4

です。　受信者Ａ３君は、これと自分に配給されたベクトル t3 との内積を計算します。　結果は

<y,t3> = < (a1t 1+ a2t2 + a3t3 + a4t4 ), t3> = a1<t1,t3> + a2<t2,t3> + a3<t3,t3> + a4<t4,t3> = 4a3

となり、Ａ３君のデータが得られます。

注１　：　ＣＤＭは直交する＋１とー１の２値パルス列を使いますが、一般に、２値に限定しない実数値でも、直交する信号は自由に作ることができます。　しかし、その長さがＮであるかぎり、直交する信号の数はＮ個以上はとれません。
注２　：　実際にＦＤＭを実現する場合、チャンネルとチャンネル間に若干のスペースを空ける必要があります。そうしないと隣接チャンネルへの干渉（漏話）の危険性があるからです。それでは、いっそうのこと、チャンネルをずらせながら重ねて、それぞれのサブチャンネルの時間領域のパルス（時間幅は広がっている！）が直交するようにできないかという発想が湧きます。これがＯＦＤＭ (Orthogonal frequency Division Multiplex)といわれるものです。　信号の直交という概念はあらゆる場面で遭遇しますので、固有値解析などのページを参照してください。