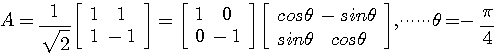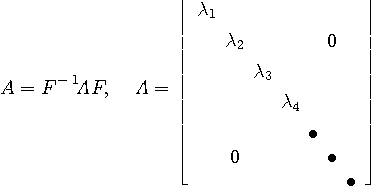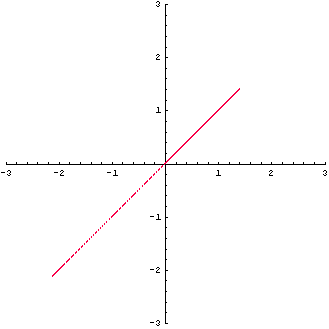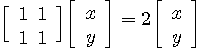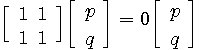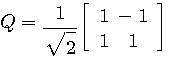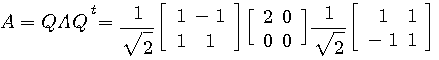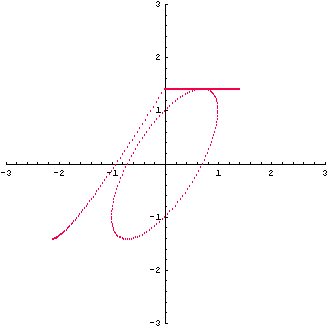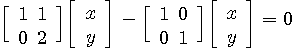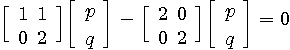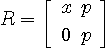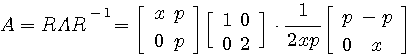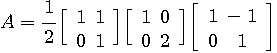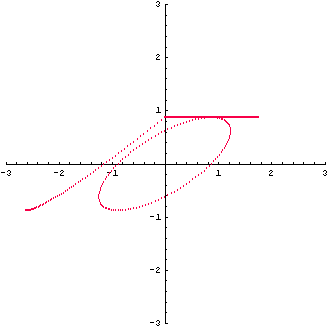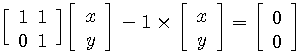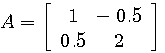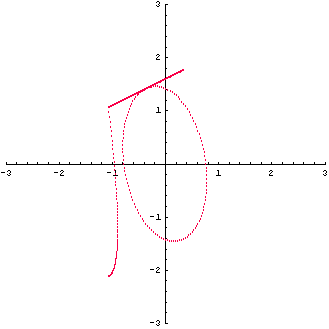|
文脈重視から定理の証明は省きますので、線形代数の参考書を読んでください。
数値の列をベクトルと定義します。 数値は電気信号をサンプルしたものから気象データや経済指標まで、なんでもありです。 ベクトルの線形変換は、一般に
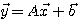
のように表すことができます。 大文字の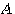 は行列、小文字の上に→が付いた記号はベクトルを表します。 は行列、小文字の上に→が付いた記号はベクトルを表します。  は単なる平行移動なので、これを除いた線形変換 は単なる平行移動なので、これを除いた線形変換
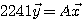
に着目します。 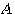 を正方行列とします。 を正方行列とします。
定義 1
行列  について、 について、

が成り立つ行列  があるとき、 があるとき、 を逆行列といい、 を逆行列といい、 で表す。 で表す。
このような  を正則行列という。 を正則行列という。
定義 2
行列の行(列)ベクトルのノルム(要素の自乗和)が1
であり、
各行(各列)が互いに直交するとき、
この行列を直交行列といい、 で表す。 定義から、次が成り立つ。 で表す。 定義から、次が成り立つ。

もし、変換 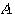 が直交行列 が直交行列 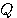 と対角行列 と対角行列 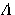 を用いて、次のように対角化できたとします。 を用いて、次のように対角化できたとします。
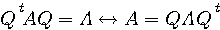
そうすると、線形変換は
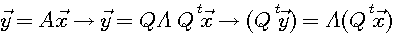
となり、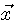 や や  を を 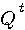 で直交変換することにより、独立なスカラー式に分離されます。 行列 で直交変換することにより、独立なスカラー式に分離されます。 行列 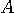 がいかに複雑でも、このように分離できれば、見通しの良い分析が可能になります。 まずは、 がいかに複雑でも、このように分離できれば、見通しの良い分析が可能になります。 まずは、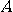 が直交行列のケースから、簡単な例題で当たっていきましょう。 が直交行列のケースから、簡単な例題で当たっていきましょう。
例(1): 直交行列
による変換。 左の青い図形が右の赤い図形に変換されました。
図形が同じ形を保存して45度の回転と反転を受けている、言い換えれば、座標軸を回転・反転して見ていることが分かります。 形が保存されることは、任意の2点間のユークリッド距離(あるいは内積)が不変であることを意味しています。 このような変換を合同変換または等距離変換と呼んでいます。 多次元の場合も含めて、次の定理が言えます。
定理 1
合同変換の行列 A は直交行列である。 逆も成り立つ。
工学で頻繁に現われる直交変換として、離散フーリエ変換やアダマール変換があります。 これらは、信号や画像に含まれる成分を分析する意味から有用です。
次に、離散フーリエ変換行列(直交行列)を  とし、 とし、
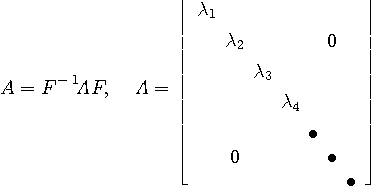
のような変換を作ってみます。 この  は、もはや直交行列ではありません。 この変換は、信号をフーリエ変換して、スペクトルに は、もはや直交行列ではありません。 この変換は、信号をフーリエ変換して、スペクトルに
 を掛けて、時間領域の信号に再び戻すという操作を表しています。 通信工学でいうフィルターの操作です。 を掛けて、時間領域の信号に再び戻すという操作を表しています。 通信工学でいうフィルターの操作です。
この逆の問題、すなわち、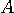 が与えられ、これを上のように対角化する問題は工学的に大変重要です。 このハイパーテキストでも、多くのページでこの問題に遭遇しています。 また、経済学や心理学の統計解析で頻繁に使われる因子分析もこの問題です。 ここでは、対称行列を扱うことが多いですが、主要因子に対応するベクトルの意味を解釈することが難しい問題となります。 加えて、行列にランダム要素が混入し、こんがらがった未知要因を解きほぐす複雑な作業になります。 非対称行列では、難しくなります。 が与えられ、これを上のように対角化する問題は工学的に大変重要です。 このハイパーテキストでも、多くのページでこの問題に遭遇しています。 また、経済学や心理学の統計解析で頻繁に使われる因子分析もこの問題です。 ここでは、対称行列を扱うことが多いですが、主要因子に対応するベクトルの意味を解釈することが難しい問題となります。 加えて、行列にランダム要素が混入し、こんがらがった未知要因を解きほぐす複雑な作業になります。 非対称行列では、難しくなります。
一般に、対角化の数学的構造は単純ではありません。 以下、2行2列の直感的な例題で、対角化の構造を把握しましょう。
例(2): 対称行列
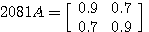
による変換。 青色が赤色のように押しつぶされてしまいました。
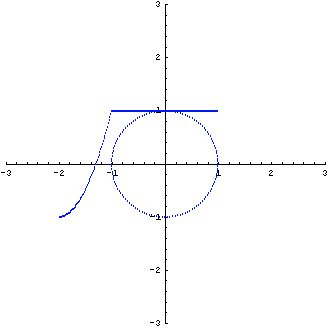
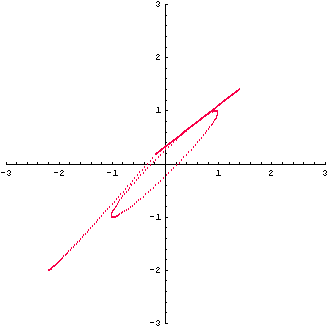
この変換は、斜めから圧縮されたことが想像されますね。 そうです、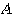 は次のように対角化できます。 は次のように対角化できます。
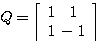
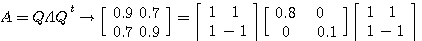
すなわち、変換 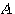 は、例(1)の直交変換をして得たベクトルの第1要素(横軸)を0.8 倍し、第2要素(縦軸)を0.1
倍して、逆変換で元に戻すことを意味しています。 対角行列の要素、0.8, と
0.1 を固有値、それに対応するベクトル (1, 1) と (1, -1) を固有ベクトルと呼んでいます。 固有値と固有ベクトルを計算で求めるならば、まず は、例(1)の直交変換をして得たベクトルの第1要素(横軸)を0.8 倍し、第2要素(縦軸)を0.1
倍して、逆変換で元に戻すことを意味しています。 対角行列の要素、0.8, と
0.1 を固有値、それに対応するベクトル (1, 1) と (1, -1) を固有ベクトルと呼んでいます。 固有値と固有ベクトルを計算で求めるならば、まず
定理 2
固有値は行列式( の多項式) の多項式)
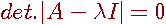
の根である。
によって固有値を求め、
定理 3
固有値  に対応する固有ベクトル に対応する固有ベクトル  は は

を満たす。
によって、固有ベクトルを求めます。
定理 4
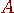 を n 次正方行列としたとき、n 個の固有値が求まる。 を n 次正方行列としたとき、n 個の固有値が求まる。
それらがすべて異なるとき、
定理3によって求めた
n 個の固有ベクトルは互いに独立になる。
もし、 が m 重根のとき、 が m 重根のとき、

を満たす独立な m 個の固有ベクトルがなければ、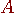 は対角化できない。 は対角化できない。
とくに、対称行列やユニタリ行列は工学的に大変有用ですが、多重根があっても、次のような直交分解の定理が成り立ちます。
定理 5
実対称行列の固有値は実数であり、直交行列で対角化可能。

このような対角化ができるのは実対称行列のときだけである。
これを複素数に拡張すると、
定義 3
転置して複素共役をとる操作を、右肩に
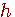 を付けて表す。 を付けて表す。
 となる行列をエルミート行列という。 とくに、実数のときは対称行列。 となる行列をエルミート行列という。 とくに、実数のときは対称行列。
 を満たす行列をユニタリ行列という。 とくに、実数のときは直交行列。 を満たす行列をユニタリ行列という。 とくに、実数のときは直交行列。
 を満たす行列を正規行列という。 を満たす行列を正規行列という。
エルミート行列もユニタリ行列も正規行列である。
定理 6
正規行列の固有値は実数であり、次のように対角化可能。

このような対角化ができるのは正規行列のときだけである。
定理5では、「直交行列で対角化が可能」と言っていますが、この言葉は次の意味を孕(はら)んでいます。
- 直交行列でしか対角化可能というわけではない。
- 直交行列が必ずしも一意に決まるわけではない。
以下は、これらを端的に示す例題です。
例(3): 単位行列
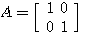
は任意の正則行列によって、

が成り立つので、任意の正則行列によって対角化可能です。 さらに、固有値が重複していますが、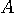 が対称行列なので直交行列(正則行列の特別な場合)で対角化されます。 が対称行列なので直交行列(正則行列の特別な場合)で対角化されます。
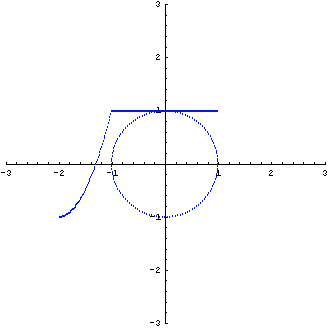
例(4)対称行列

は非正則(ランクが1)です。 図形の変換は下のように直線になってしまいました。
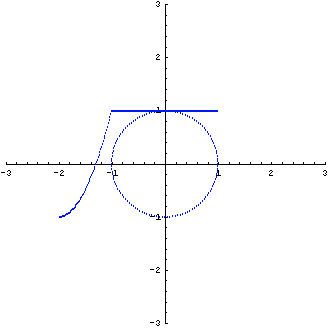
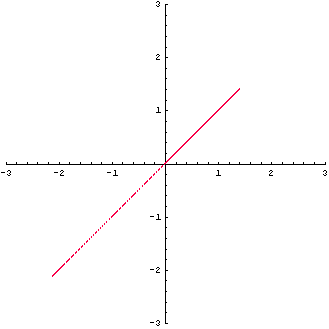
この対角化を進めてみましょう。 まず、固有値は
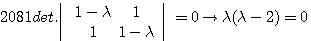
より、2 と 0 です。 2 に対する固有ベクトルは
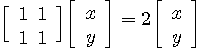
から、 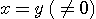 となります。 0 に対する固有ベクトルは となります。 0 に対する固有ベクトルは
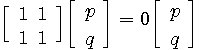
なので、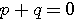 です。 よって、対角化は です。 よって、対角化は
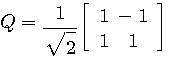
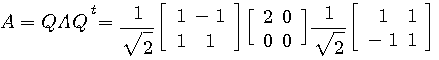
のようになりました。 直交変化した後で、1番目の成分が2倍され、2番目の成分が消えて、直線になったわけです。
行列 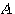 が対称でも正規でもない場合、直交行列やユニタリ行列での対角化は不可能です(定理5)。 もし、どうしても直交行列やユニタリ行列で展開したい場合は、三角化することになります。 が対称でも正規でもない場合、直交行列やユニタリ行列での対角化は不可能です(定理5)。 もし、どうしても直交行列やユニタリ行列で展開したい場合は、三角化することになります。
定義 3
対角項の下のすべての要素がゼロである行列を上三角行列といい、D
で表す。
対角行列はその特別な場合である。
定理 7
複素正方行列は

のように三角化可能。
とくに、すべての固有値が実数のときは、

上三角行列 D の対角項は固有値である。
例(5): 三角行列
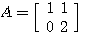
の固有値は 1 と 2 です。 図形の変換は下図のようです。
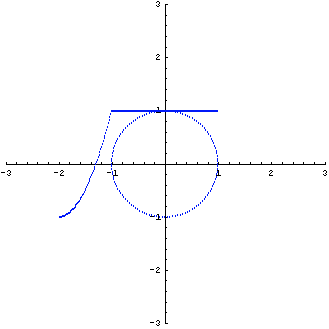
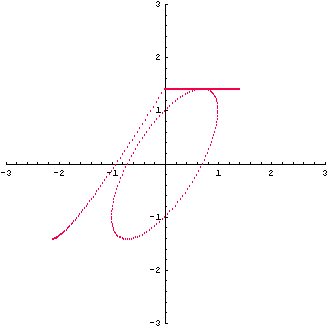
固有値が異なっているので、定理4から対角化可能です。 ただし、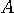 は対称行列ではないので直交行列による対角化はできないはず。 固有値 1 に対する固有ベクトルは は対称行列ではないので直交行列による対角化はできないはず。 固有値 1 に対する固有ベクトルは
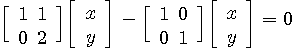
から、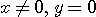 。 固有値 2 の固有ベクトルは、 。 固有値 2 の固有ベクトルは、
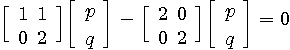
から、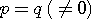 。 したがって、 。 したがって、
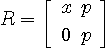
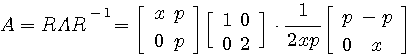
 > とすれば、正則行列による対角化は次のようになります。 > とすれば、正則行列による対角化は次のようになります。
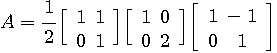
例(6):三角行列
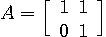
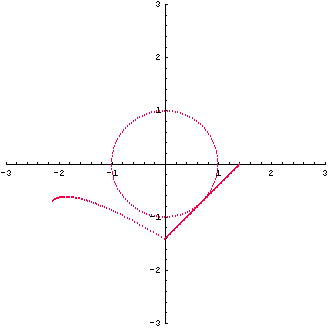
の固有値は 1 で重複しています。 図形の変換は下図です。
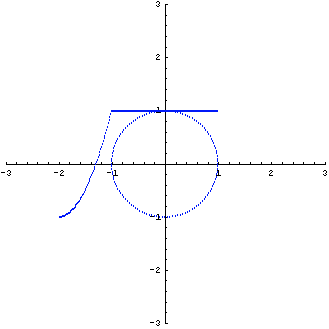
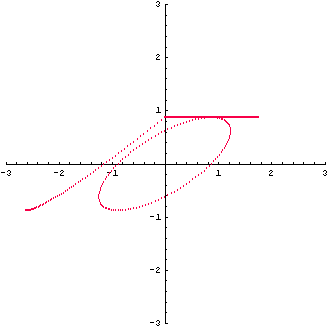
固有ベクトルは
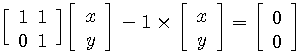
から、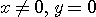 のみです。 したがって、対角化不可能です。 三角化は のみです。 したがって、対角化不可能です。 三角化は
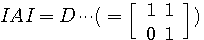
のみです。
例(7): 三角行列でない対角化不可能な例として、
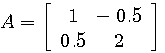
この変換の様子を描いてみると下図のようです。
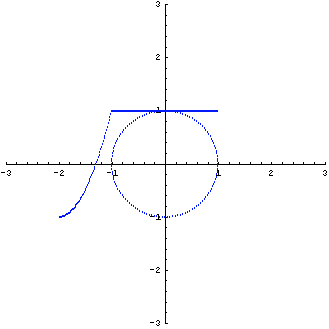
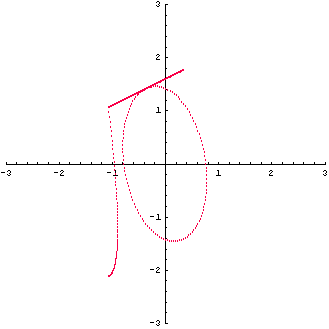
固有値は 1.5 で重複しており、対応する固有ベクトルは 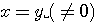 > だけなので対角化できなません。 三角化は次のようです。 > だけなので対角化できなません。 三角化は次のようです。
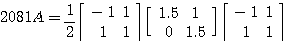
注: 正則行列
 は Gram-Schmidt の正規直交化法によって は Gram-Schmidt の正規直交化法によって  の形に分解できる。 このような三角化は最小2乗法において有用である。 の形に分解できる。 このような三角化は最小2乗法において有用である。
|