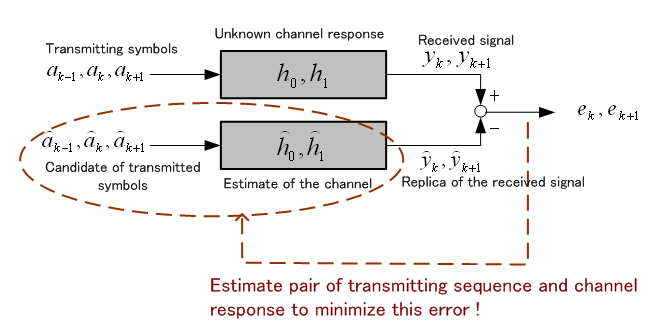
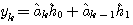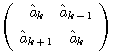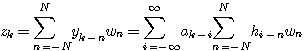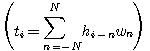|
ブラインド問題 Entrance to the Blind Problem |
|
深夜の摩天楼で銃が乱射された。犯人は車を走らせ、機関銃のように撃ちまくった。 偶然一人の少年が、自宅で銃声を録音していた。 警察はそのテープを入手したが、わわっわ〜んゎ〜〜わ〜ゎわ〜んっんゎ〜 という音だけ。 なんとかして、銃撃の間隔や回数を割り出そうと考えた。 銃の発射音は反射・回折を繰り返し、長くこだまを引いて少年の部屋まで到達する。 反射・回折の様子は時間とともに変化し、復元することはできない。  銃を携帯電話、録音機を基地局と考えれば、これはまさに移動体通信と同じ問題です。 一般に、 システムの出力信号だけから入力信号(またはシステムの特性)を推定せよ ということになります。 このような問題を ”ブラインド問題 ( Blind Problem )” と呼んでいます。 移動体通信のみならず、有線通信もまったく同じですが、通信は本質的にブラインド問題なのです。 ブラインド問題は、なんの付帯条件もなしに解くことはできません! ここでは、一入力・一出力の場合について解説します。 まず、システムは、入力
の左辺だけを受け、右辺は隠されています。 一般に、左辺から右辺の二つの変数を求めることはできません。 でも、もし入力が二つの値
しかとらないこと(多値の場合にも一般化できますが、説明の簡単のため2値とする)、および、
で表します。 下付きの添字は時刻を表します。未知システムは線形であり、そのインパルス応答(冒頭の一発の銃声のこだまに相当)が2時刻で終わるとします。 そうすると、受信信号は
のように与えられます。 もちろん右辺は隠されています。 この場合、 右辺に含まれる送信データの組み合わせは
の4通りですが、これらすべてについて、
の右辺で作ることができますね。 したがって、すべての組み合わせが送信された可能性があり、送信データを一意に特定することができません。 それでは、もう一つ時刻を足してみましょう。
上の連立一次方程式に含まれる送信データのパターンは次の8通りです。
これらのパターンが送られたと仮定して、上の連立方程式を満たす解
でも、ちょっと考えれば、やはりダメなことがわかります。 それぞれのパターンについて、行列
が正則(行列式が非ゼロ)と非正則(行列式がゼロ)に分類されます。 このうち、正則になるパターンは次の4つです。
このとき連立方程式は一意解をもつので、この4つのパターンは無条件に送信された可能性があり、捨てることができません。 このことから、2時刻分の連立方程式でも送信信号を特定できないことが分かります。では、もう一つ加えて、
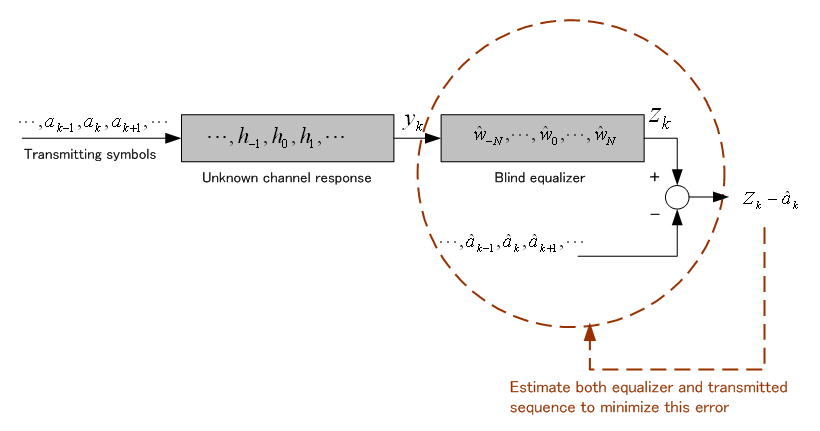
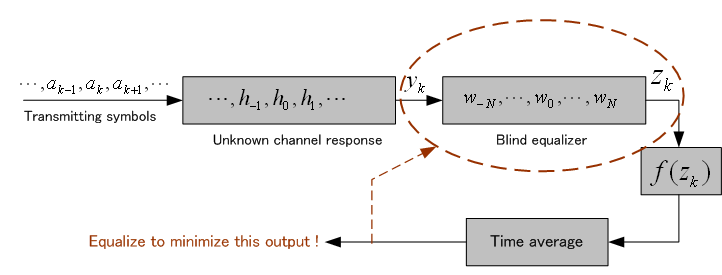
ではどうでしょうか? もう、複雑ですね。 ケイタイするのに、こんな難しいことが必要なの? と言いたくなります。 このような解法をブラインド系列推定と呼んでいます。 これが解けないとケイタイすることができません。 移動しながらケイタイを使っている以上、この問題はなんらかの方法で解かれているはずなのです。詳しくは、解説論文、 PDF (信号処理学会、Journal of Signal Processing Vol.3, No.4, July 1999 ) を参照してください。なお、雑音がある実際の場合のブラインド系列推定は、論文 Sato,Y, "A Blind Sequence Detection and Its Application to Digital Mobile Communication", IEEE Journal on Selected Areas in Communications, Vol.13, No.1, pp.49-58, 1995) を参照してください。 一方、このブラインド系列推定と逆のモデルを考えることができます。 それは、受信信号をブラックボックス(チャンネル)の逆システムに入力して、送信信号を得るようにすればいいわけです。 ちょっとややこしいですが、下図のような逆システムを求めるモデルです。 このようにな問題を通信では等化 (Equalization ) と呼んでいます。 他の分野では、逆コンボリューション (Deconvolution ) と呼んでいます。歴史的には、この問題が先に開発されました。
以上は、不確定な外乱を無視したモデルですが、 さて、この等化のブラインド問題を、先のブラインド系列推定の手法を用いて導くこともできますが、これを有線通信などで推し進めようとると、実は絶望的になってしまいます。 その理由は、波形歪みや雑音などが小さい有線通信では小さなロールオフ率と大きな多値数で高速ディジタル伝送を実現しています。 パルスは30〜60シンボルぐらいの裾を引き、多値数は4以上になります。 受信信号は、たとえば、
のようになります。 こうなると、ブラインド系列推定の計算量は莫大になってしまいます。 代数的な方法ではなく、もっと簡単なモデルで問題を解決しなければなりません。 この手法は、受信信号だけから、時間をかけて、統計的手法で、チャンネルの逆システムを推定しようというものです。 この問題をブラインド等化と呼んでいます。 有線通信の高速ディジタル通信ではこの手法が広く実用されています。チャンネル応答
の逆応答(等化器)を受信信号だけから推定できれば、等化器の出力は送信シンボル系列に等しくなります。詳しくは、解説論文 PDF (信号処理学会、Journal of Signal Processing Vol.3, No.5, September 1999 ) を参照してください。 理論の概略は次のようです。等化器の出力は
ですが、ある統計的評価関数
が最小(または最大)になるように等化器の重み係数
が実現できるようにすることです。 このような解法が成立する十分条件の例として、次のようなセットを挙げることができます。 (1) 送信信号は I I D (Independent Identically Distributed)
である。 この条件は、ブラインド等化の手がかりを暗示しています。 直感的にいえば
ということです。 ブラインド等化のテーマは、等化目標を果たす非線形関数
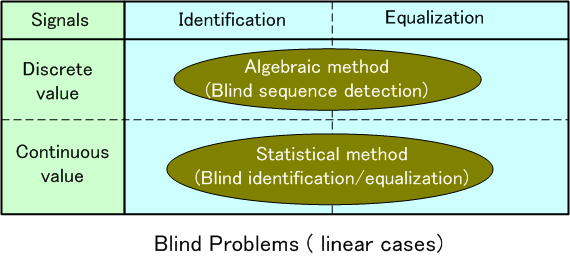
以上を簡単に整理すると、下の表のようになります。
注1: システムの同定ができるならば、それから逆システムが簡単に算出できるので、等化を考える必要がないと思うかも知れません。 逆に、等化ができれば同定は必要ないと考えられます。 移動体通信のように、レイリーフェージングによって逆システムの存在が保証されない場合には、どうしても同定法を選択せざるをえません。 |
 を
を 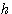 倍して
倍して 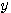 を出力するとします。 われわれは
を出力するとします。 われわれは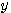 から
から  も
も 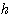 も確定することができます。 では、チャンネルに記憶があると(銃声が長く反響を繰り返すと)、どうなるでしょうか? 話は簡単ではなさそうだけど、ちょっと見てみましょう。 送信データを2値(
も確定することができます。 では、チャンネルに記憶があると(銃声が長く反響を繰り返すと)、どうなるでしょうか? 話は簡単ではなさそうだけど、ちょっと見てみましょう。 送信データを2値(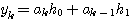
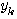 も
も