|
周波数分析（短時間フーリエ変換） Frequency analysis |
|
音波は、鼓膜を振動させ、リンパ液で満たされた蝸牛（カタツムリ）管を伝播し、蝸牛管を縦に仕切るように張られた膜を共振させます。 膜には長軸と直角に無数の繊維が通っており、膜の振動を受容します。 長軸方向に膜の共振周波数が変わるようになっており、膜のどこが共振するかというパターンが音に含まれる周波数成分のパターンに一致し、ぼくたちはそれを知覚して音楽を聴いたり、話を聞いたりしています。 聴覚の生理学に関する詳しい内容は 聴覚受容の機序：http://www.tmd.ac.jp/med/phy1/ptext/ear_1.html を参照してください。 注１： 音を聴くということは、音源そのものを聴くというだけでなく、音源の位置や移動を聴くことも含まれます。 片方の耳だけでは、周波数スペクトルの強さを認識しますが位相特性の認識は苦手です。 両方の耳で聴いてはじめて、音源の位置や移動を立体的に認識することが可能になります。 音源から両耳の鼓膜にいたる複雑な伝播の伝達関数を正確に作り、それをヘッドフォンで鼓膜に供給してやれば、完全な（全方位の）３Ｄサウンドを製作することができます。 たとえば、下のページに３Ｄサウンドがあります。 できれば、ヘッドフォンで聴いてみてください。 ３Ｄサウンド：http://www.arns.com/ 数学的にいう周波数は、過去から未来へ永遠に単振動するという概念です。 しかし、周波数の大きさや位相が変化してはじめて、ぼくたちは音楽を楽しみ、人の話を聞くことができます。 一方、ぼくたちの耳の中で振動する膜もまた、有限時間内に共振が収まらなくてはなりません。 そうでないと、いつまでも耳の中でワーンという残響が残ってしまい、音楽を聞くどころではありません。 時間的に変化する周波数成分を分析するためのフーリェ変換を以下のように定義します。
は矩形の窓関数です。 ちょうど四角形の窓から外を流れる風景を眺めるようなものです。
しかし、このように不連続に切り取る窓関数では、 窓関数の時間幅が広いと、周波数の識別能力が上がることは直感的に予想がつきます。 その反面、周波数の変化を読み取る精度は落ちそうです。 このことは、残響の長い部屋で速いテンポの音楽が聞きづらくなることを想像すれば容易に理解できます。 具体的に、ガウス窓関数
を使って確かめてみましょう。 分散
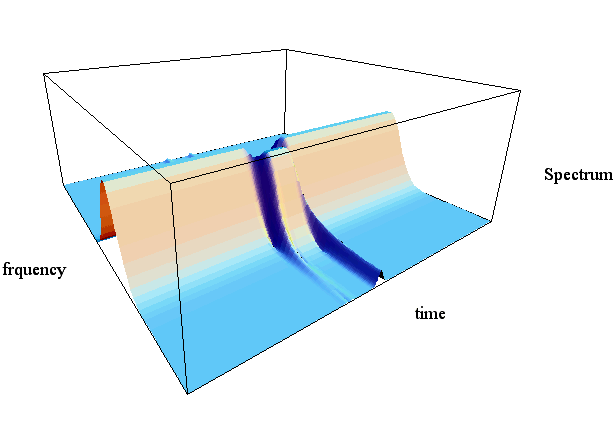
下図は、窓の時間幅が広い場合と狭い場合の
上の図の窓が広い場合は、スペクトルの山は周波数軸方向で急峻であり、時間軸方向でゆるやかです。 したがって、周波数が精度良く識別できる反面、周波数の切り替え時刻があいまいになっています。 逆に、下の図の窓が狭い場合は、スペクトルの山が周波数軸方向でなだらかになり、時間軸方向で急峻になっています。 したがって、周波数の識別能力が落ちる反面、切り替わりの時刻を速やかに検知します。 このことは、 周波数と時間との間には、 ことを示唆しています。 これを信号の（ハイゼンベルグの）不確定性原理と呼び、ぼくたちの耳も目も、そしてどんなに性能の良い測定器も、この原理に従わざるを得ません。
注２： ２次元関数
注３： 不確定性原理の具体的な限界を引き出すためには、パルスあるいは窓関数について、時間の広がりと周波数の広がりを具体的に定義しなければなりません（パルスの不確定性を参照）。 注４： この周波数分析に似た変換として離散ウェーブレットがあります。 これは、信号の時間変化の局所的性質に合わせて、窓関数を伸縮しようというものです。 連続ウェーブレットについてはデルタ関数で触れています。 注５： 窓関数として標本化関数を選ぶと、帯域制限の概念が得られ、これによって標本化定理が導かれます。 注６：Wiener-Khintchine
の定理を短時間フーリエ変換
|
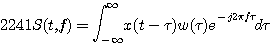
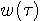は有限の広がりをもった窓関数といわれるもので、膜の共振が持続する時間幅に相当しています。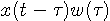 
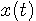を窓 
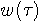をスライドさせながら見ていることを意味します。 時間の経過とともに、窓から見える風景が移り変わり、その風景を時間の経過にしたがって分析しようというわけです。 たとえば、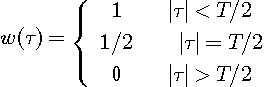
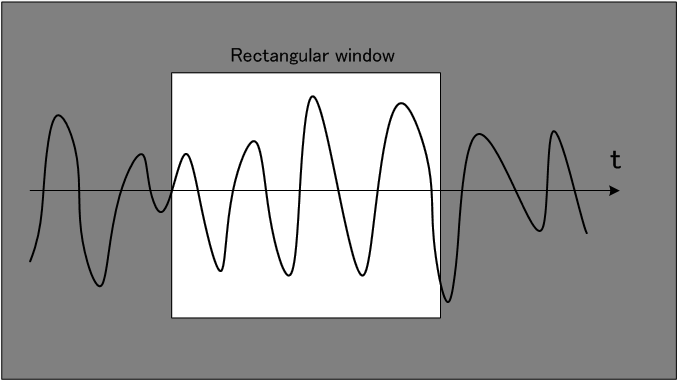
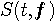が振動的になり精度のよい周波数分析ができません。 そこで、境界をできるだけなだらかにした窓関数を使います。 いろいろな窓関数が考案されていますが、対象とする信号の性質や分析の目的に応じて個別に設計するのがいいでしょう。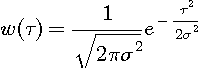 
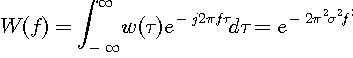
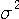を大きくすると、
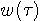の時間幅は広がり、
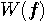の周波数幅は狭まります。 この窓関数を使って、二つの発振器を瞬間的に切り替えたときの信号
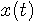を分析してみます。 この「切り替え」は下のような線図で表現できます。 この図は、あくまでも周波数の「切り替え」の概念的な説明図であり、われわれはこのような「切り替え」をどこまで認識できるかどうかを問題にしていることに注意してください。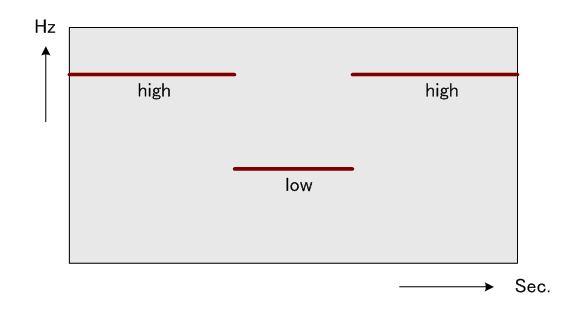
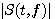を示しています。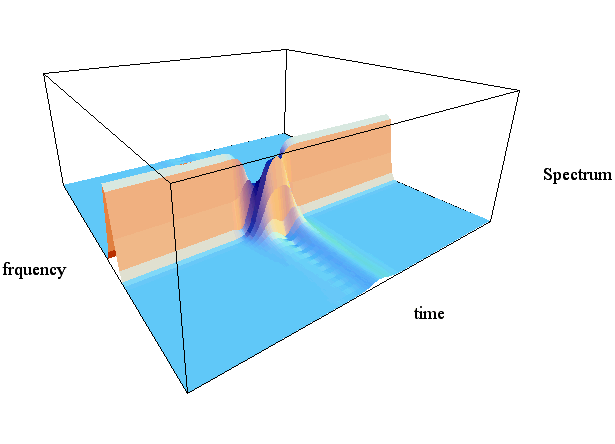
は１次元関数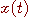 
を拡大写像したものですから大きな冗長を含んでいます。 逆変換 
は２次元から１次元への縮退写像になります。 これについては、
から導くと、直感的理解が容易である。