

|
ナイキストパルス Nyquist Pulse |
|
ほとんどの通信では、使用する周波数帯域が決められており、この帯域の外に漏洩する送信スペクトルの上限が厳しく制限されています。 ディジタル通信はパルスを使って情報を送りますが、このパルスのスペクトルを、下図のような余弦ロールオフで設計するのが一般的です。
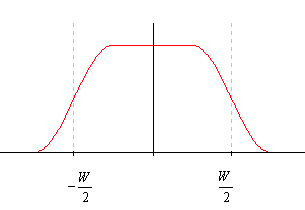
余弦ロールオフ 上図の使用帯域幅
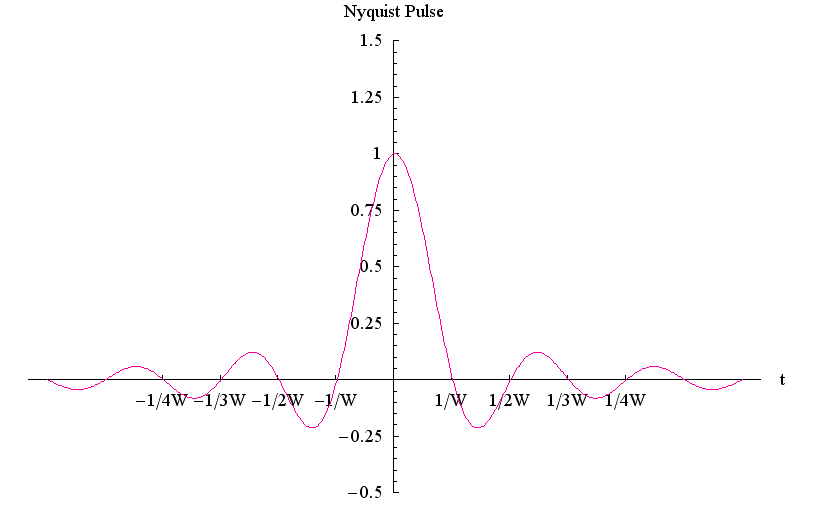
このパルスの形をよく見ると、ピーク以外で等間隔にゼロ交叉していることがわかります。この条件をナイキスト条件と呼び、これを満たすパルスをナイキストパルスと呼んでいます (Harry Nyquist, 1889-1976) 。 実際のディジタル通信では、ナイキストパルスが送信機から送り出されますが、等間隔ゼロ交叉の性質が重要な働きをしているのです。 たとえば、正のパルスと負のパルスでディジタル情報を送ることを考えてみてくだい。 もし、パルスの裾が十分減衰してから次のパルスを送り出すことをすれば、単位時間に送れるパルスの個数は少なく、伝送速度は非常に遅くなります。 しかし、2値(正または負)パルスを1/W秒の周期で次々と送れば、パルスがゼロ交叉する時刻において、前後のパルスからの干渉を受けません。このような送り方をすれば、1秒間にW個のパルスを正確に送ることができます。これが、高速ディジタル通信を実現する一つの重要なポイントなのです。 ナイキスト条件を満たすパルスは無限に作ることができます。 パルス
のようになります。ナイキスト条件は、すべての整数
を満たすことです。 この条件をパルスのスペクトル
ですが、
のように変形できます。 この形は{ }内の関数をフーリエ級数展開していることを表しています。 すべての
となります。 もし、
のようにわかり易い形に書けます。 一般に、
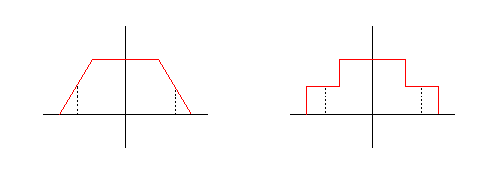
直線ロールオフと階段ロールオフ さて、ナイキスト条件を満たすパルスを用いた送信信号を視覚的に見てみましょう。
送信シンボルを
のように与えられます。 これを、現在時刻
となり、第1項が現在時刻に送られたシンボルの情報を表し、第2項は前後のシンボルに起因するランダムな不要成分を表しています。 この項を符号間干渉
(Inter-symbol interference ) と呼んでいます。 もしパルスが等間隔ゼロ交叉していれば、第2項は必ず消滅しますから、正確にシンボル
で
のように遅れた位相でサンプルすると、現在時刻
のようになり、第2項の符号間干渉は非ゼロとなりシンボルの判定誤りを引き起こします。 この様子を視覚的に理解するために、アイパターンを描きます。 これは、現在時刻を中心とする時間区間
4値アイパターン 中央に開いた3つの空白の領域をアイ(eye)と呼んでいます。 アイが開いていれば、この中央でサンプリングすれば正確にシンボルが判定できます。 もし、サンプリング位相 がゼロでなければ、アイの中央からずれてサンプリングすることになり、正確なシンボル判定ができません。 そして、サンプリング位相が限界を超えると、シンボル判定が確実に誤ることが分かります。 サンプリング位相を、ちょうどアイがもっとも開いている位置にコントロールすることをタイミング位相制御と言っています。 ただし、パルスがチャンネルを通過すると必ずチャンネル歪を受け、せっかく送信信号がナイキスト条件を満たしていても、受信時点でアイは閉じてしまいます。 こうなると、どこでサンプリングしてよいか分からなく、タイミング位相制御する意味もなくなり、大変困難な壁にぶっつかります。 この問題は、まさにモデム設計の重要なポイントであり、いろいろな判定理論(等化器、最尤系列推定、最大事後確率判定など)につながります。 |
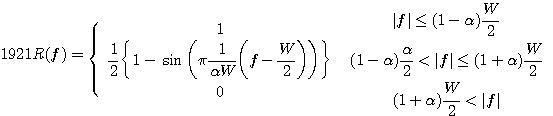
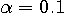 ) としてフーリェ逆変換すると、下図のようなパルスが得られます。ディジタル通信では、このように振動しながら減衰するパルスを用いています。
) としてフーリェ逆変換すると、下図のようなパルスが得られます。ディジタル通信では、このように振動しながら減衰するパルスを用いています。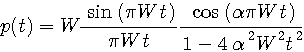
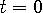 を中心に周期
を中心に周期 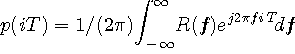
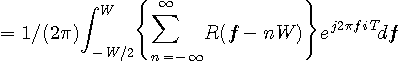
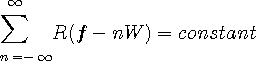
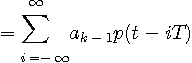
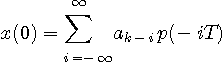
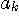 を受信することができます。
を受信することができます。