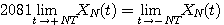|
信号の自由度 Freedom of signal |
|
信号の周波数帯域幅と時間幅を制限すると、 一般に、答えは「ノー」ですね。 たとえば、帯域制限を受けた有限エネルギーの信号は永遠に尾を引きます(帯域制限パルスを参照)。 逆に、有限時間で終わる信号は無限の周波数成分をもつはずです。 答えを「イエス」にするためには、周期信号を対象にしなければなりません。1周期区間をとれば、信号の情報がすべて含まれていおり、帯域制限されていれば、標本化定理によって有限個のサンプルで済みます。 時間幅を
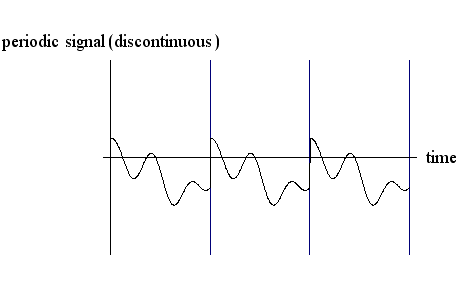
とし、帯域幅が 周波数のページでみたように、周波数は、「過去から未来にわたる永遠の単振動」を数学的に定義しています。 したがって、下の右図(縦軸は帯域幅)のように、時間によって帯域幅が変化するという図はあり得ないわけです。 ただ、音声や音楽の波形を短時間で切り取り、その区間内の周波数成分を分析することは普通に行われています。 これはこれで、実用的な近似の話です(周波数分析を参照)。
注: 帯域幅が自在に変化する信号をもっとも効率よく(もっとも少ないパラメータで)表現する手法としてウェーブレットがあります。局所的に自由度が高いところでは速くサンプリングし、低いところではゆっくりサンプリングすればよいという考えを一般化しようとするものです。 フーリエ級数展開は周期信号を対象にして、その基本周期に含まれる周波数成分を記述するものです。 長さ
この信号が周波数幅
となります。 フーリエ係数
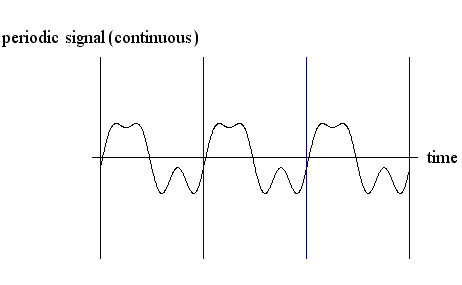
は明らかです。 すなわち、図1のように連続的な周期信号でなければなりません。 図2のように時間幅の端点で不連続な周期信号は無限個のフーリエ係数を必要とします。 フーリエ係数を増やすにしたがって不連続点を近似する様子は Gibbs Oscilation を参照してください。
図1
図2
|
 秒(
秒(  は整数)とし、この区間内の複素信号を
は整数)とし、この区間内の複素信号を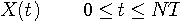
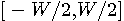 に制限されているならば、
に制限されているならば、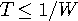 秒毎に
秒毎に 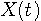 をサンプルして得られる
をサンプルして得られる  個のサンプル列から、元の連続信号
個のサンプル列から、元の連続信号 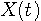 を完全に復元することができます。 逆に、
を完全に復元することができます。 逆に、 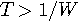 でサンプルしてしまうと、元の信号を正確に復元できません。 したがって、
ちょうど
でサンプルしてしまうと、元の信号を正確に復元できません。 したがって、
ちょうど 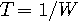 秒として、帯域
秒として、帯域
 の複素信号を
の複素信号を  秒周期で
秒周期で  個サンプルして得る次元ベクトルはその複素信号を過不足なく表現しています。 このことから、この複素信号の自由度は
個サンプルして得る次元ベクトルはその複素信号を過不足なく表現しています。 このことから、この複素信号の自由度は
 であると言えます。
であると言えます。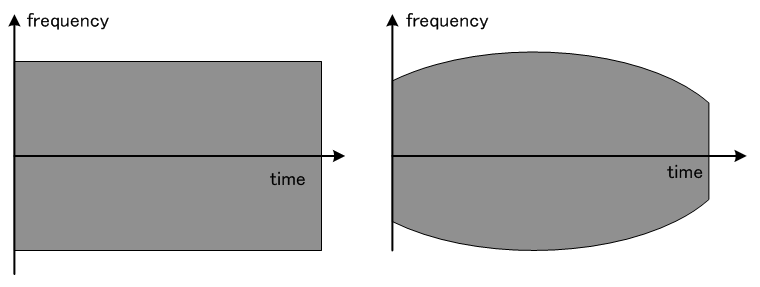
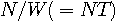 秒の任意の連続な複素信号は以下のように一意にフーリェ級数展開できます。
秒の任意の連続な複素信号は以下のように一意にフーリェ級数展開できます。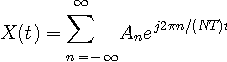
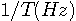 に制限されていると、
に制限されていると、 は
は 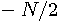 から
から
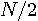 > までです。 しがって、
> までです。 しがって、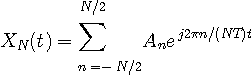
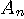 の個数は
の個数は
 になり、周波数領域では自由度が一個多くなりました。 帯域端の解釈や時間幅の端点の解釈の違いによって、このように
になり、周波数領域では自由度が一個多くなりました。 帯域端の解釈や時間幅の端点の解釈の違いによって、このように
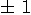 の差が出ます。 普通は、時間幅を十分大きくとって、この差を解消します。 では、上のように有限個のフーリエ係数で表現された周期信号はどんな形をしているでしょうか? 基本周期の端点に注目すると、フーリエ係数の個数が有限なので、
の差が出ます。 普通は、時間幅を十分大きくとって、この差を解消します。 では、上のように有限個のフーリエ係数で表現された周期信号はどんな形をしているでしょうか? 基本周期の端点に注目すると、フーリエ係数の個数が有限なので、