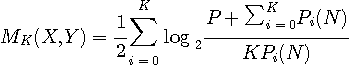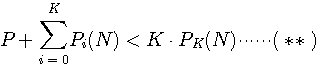|
注水定理 Water Pouring (or Filling) Theorem |
|
注水定理は次の疑問に答えるものです。 有色雑音が加わるチャンネルに対して、 このような問題は、CATVの上り回線における流合雑音を避ける場合や、無線通信において使用チャンネルを自動的に避ける場合や、PLC (Power Line Communication) で漏洩電波を出さないようにする場合など、多くの局面で遭遇します。 注水定理を実現し易いディジタル伝送方式として、OFDM や THP(Tomlinson Harashima Precoder)を参考にしてください。 本題に入る前に、ランダム信号に関する基本的概念を整理しておきます。 <ガウス信号>
で与えられるということです。 <独立>
が、前後の信号に影響されずに、独立に生起するとき、その信号は独立であるといいます。 とくに、いつも同じ確率分布にしがう場合をI I D(Independent Identically Distributed )と呼んでいます。 <無相関>
は、n 時刻遅れた信号との自己相関を表しています。 n 時刻先行する信号値との積をとっても同じですから、自己相関は
を満たします。 ここで、信号が発生する確率的メカニズムが時間的に変化しないことを仮定しておきます。 確率的メカニズムが変化しないという概念は定常と呼ばれていますが、いろんなレベルで定義されます。 まず、強い意味の定義を用います。 すなわち、有限時間区間で、信号値がしたがう同時確率
が、どの時刻をとってみても同じとします。 したがって、自己相関は
で計算されます。 強い意味で定常でなければ、
のようになっていれば、その信号は無相関であるといいます。 独立で、信号の平均値がゼロならば、必ず無相関です。 逆に無相関だからといって独立であるとはいえません。 <電力スペクトル>
自己相関は対称ですから、その電力スペクトルはかならず実数です。 無相関ならば、そのフーリエ変換はフラットですから、どの周波数成分も同じだけ含まれていることを表します。 このようなランダム信号を白色であるといいます。 逆に、無相関でなければ、そのフーリエ変換はフラットにならず、周波数成分に偏りがあることを表しています。 このようなランダム信号を有色であるといいます。 白色ならば無相関ですが、無相関だからといって独立であるとはいえません。 <多次元ガウス信号>
ここで、
であり、 <多次元ガウス信号のエントロピー>
で定義しました(アナログ信号のエントロピーを参照)。 そして、これを最大にする分布は正規分布でした。 このときのエントロピーを計算すると次のようになります。
ここで
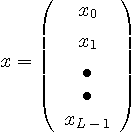
で定義され、この最大を与える分布は多次元ガウス分布です。 このときのエントロピーは次のようになります。多次元変数ベクトルを
第1項の多重積分は上で求めた式(*)になり、
となります。 この形は、自然数や円周率を含み、あまりすっきりしていません。 しかし、ここでは、数値的評価が系列長 L を固定して行われるので、ゲタを履くだけの項を省いてしまって、下式でエントロピーを評価することになります。
<エントロピーの電力スペクトル表現>
で与えられます。
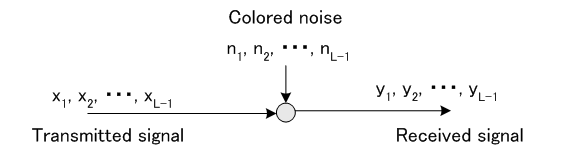
----------------- Theorem ------------------ 以上の概念を用いて、冒頭の疑問に対する解答を次のように導くことができます。 まず、対象とするモデルを下図に示します。
送信信号も雑音も有色ガウス信号であり、互いに独立であり、雑音は加算されるとします。 したがって受信信号もガウス信号です。 図中の3つの信号のエントロピーはそれぞれ次のようになります。 ここで、たとえば、
さらに、条件付エントロピー(送信信号に加わる不確定さ)はガウス雑音の加算のみによって生じるので、
となります。 したがって、相互情報量は
となり、この相互情報量を送信電力一定の条件
の下で最大化するような正の電力スペクトル
を解けば、求める送信スペクトルが得られます。 この問題は、次のような典型的な配分問題と同じです。 原料の総量をPとする。 この問題の解法として、以下に示すギッブス(Gibbs)の方法が有効です。 ギッブスの意味するところは次のようです。 最適配分の解は、ゼロと非ゼロに分けられ(全部非ゼロかもしれない)、 この原理を適用してみましょう。 解法の手順は以下のようです。 Step1: Step2:番号
から Step3:上で に代入して、 Step4:これらの結果を相互情報量に代入する。 その結果は次のようになる。 Step5:もし、
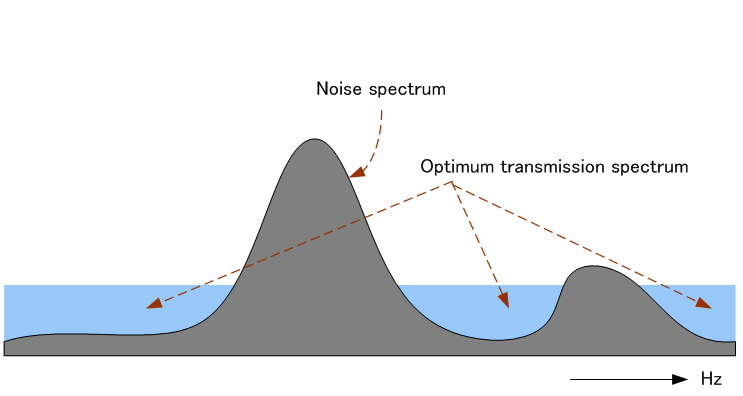
となっていれば、最大値から減少したことがいえるので、一つ前の 不等式(**)は極めて分かりやすい操作を意味しています。左辺は雑音スペクトルを地形とすると、その上から容量Pの水を注いだときに池ができます。 その水面の真下へ、水と地形からなる総容積を示しています。右辺は、順位Kまでの最大スペクトルを深さとし、その地点を高さとする矩形の総容量を表しています。 結論すると次のようにいえます。 送信パワーの制限下において、
注1:送信信号スペクトルの上限が制限される条件下 (PLCなど)では、上限値のフラットスペクトルを送信することが自明の最適である。 注2: ユークリッド距離の下で情報量が定義され、定理が証明された。 この定理がディジタル通信(ハミング距離)にどのように活かされるかは別問題であるが、近似的に適用可能である(ディジタル通信の速度限界を参照)。 注3: 受信信号にフィルター操作などをすると、注水定理のモデルが崩れてしまう。 受信信号を加工せずに、直接的に情報を引き出すことが大前提である。どのようにすればよいかに関して、この定理はなにも述べていない。正攻法はMAP(最大事後確率判定)である。 注4: 信号がガウス的であるという仮定は適用範囲を狭めてしまいます。 注水定理の導出過程で送信信号のガウス性が有効に働いた部分は、送信信号系列のエントロピーが相関行列で簡単に表現できた個所です。 任意分布について、もし系列のエントロピーが相関行列で表すことができれば、非ガウスの場合に定理を拡張することができます。 注5: チャンネルの周波数特性がフラットでない場合は、雑音電力スペクトルを『雑音電力スペクトル/チャンネル周波数特性の二乗』と看做せばよい。 注6: 実は、最適スペクトルから少々変形しても相互情報量はあまり変わらない。 相互情報量の曲面は平坦な台地状をしていて、台地の端で急峻な崖となって落ち込む。 崖から落ちるケースは、ある帯域への電力配分をカットした場合である。 注7: 現実には、雑音やチャンネル特性の時間変動が無視できない場合がある。送信スペクトルを最適化するのはなかなか難しい。 |
 とすると、それが生起する確率が、
とすると、それが生起する確率が、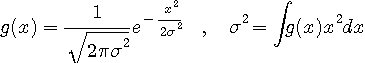
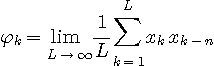
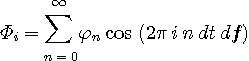
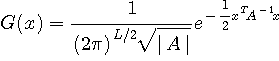
 、
、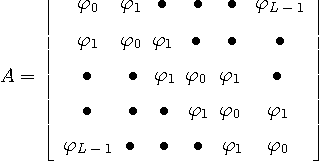
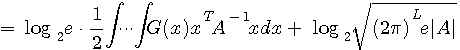
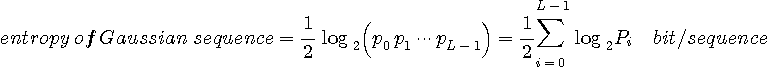
 番目の周波数の電力スペクトルを表します。
番目の周波数の電力スペクトルを表します。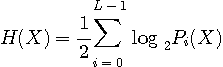
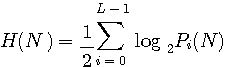
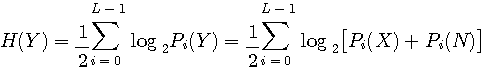
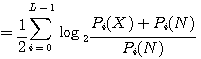
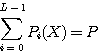
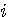 を振り直す。
を振り直す。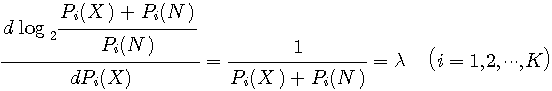
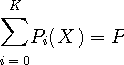
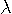 を決める。
を決める。