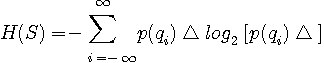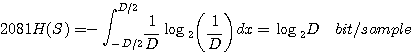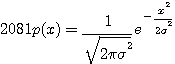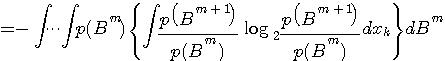|
まず、アナログ信号 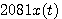 を を  秒間隔でサンプリングします。 k番目のサンプル値 秒間隔でサンプリングします。 k番目のサンプル値 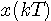 を を 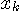 で表し、この時系列を で表し、この時系列を
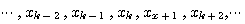
で表します。 この時系列を滑らかにつないでいた元の連続波形は捨てられてしまいます。
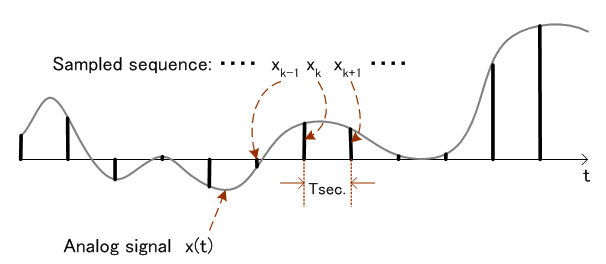
でも、もし次の標本化定理が満たされていれば、上の時系列からアナログ信号
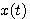 を正確に復元することができます。 を正確に復元することができます。
標本化定理
信号  が が  未満の周波数成分しか含んでいなければ、 未満の周波数成分しか含んでいなければ、
それを 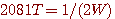 秒以下の間隔でサンプリングした時系列から 秒以下の間隔でサンプリングした時系列から
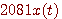 を正確に復元することができる。 を正確に復元することができる。
この標本化定理が満たされているとき、サンプリング系列は元のアナログ信号の情報をなにも失っていません。
したがって、
この時系列について情報量を定義すれば、
それは元のアナログ信号の情報量を定義したことになります。
サンプルされた値
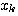 は連続的な値をとり得ます。 したがって、情報を測るで定義したような、シンボルに対する情報量をそのまま適用することができません。 実際、連続値をいくらでも正確にとることができれば、平均情報量は無限大になってしまいます。 しかし、我々が観測できる信号値はなんらかの不確定性をもっています。 それは、情報源の確率的不確定性であったり、工学的にAD変換したものであったりします。 まずは、いずれかの不確定性を導入して処理する必要が生じます。 そこで、サンプル値 は連続的な値をとり得ます。 したがって、情報を測るで定義したような、シンボルに対する情報量をそのまま適用することができません。 実際、連続値をいくらでも正確にとることができれば、平均情報量は無限大になってしまいます。 しかし、我々が観測できる信号値はなんらかの不確定性をもっています。 それは、情報源の確率的不確定性であったり、工学的にAD変換したものであったりします。 まずは、いずれかの不確定性を導入して処理する必要が生じます。 そこで、サンプル値
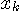 を量子化するAD変換を想定します。 量子化の幅を を量子化するAD変換を想定します。 量子化の幅を で表わし、区間の中央値 で表わし、区間の中央値
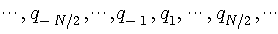
でサンプル値を近似します。 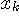 の確率密度関数を の確率密度関数を 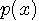 とすると、十分細かい量子化のもとでは、中央値 とすると、十分細かい量子化のもとでは、中央値 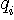 の生起確率は近似的に の生起確率は近似的に 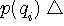 で与えられるので、この中央値を受けたときの情報量は で与えられるので、この中央値を受けたときの情報量は
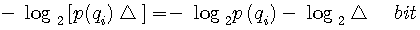
のようになります。 ここで、右辺第2項は量子化の幅  だけに依存しています。 だけに依存しています。
(A) 無記憶アナログ情報源のエントロピー
アナログ信号をサンプルした時系列
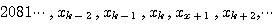
が独立であり、常に同じ確率分布に従うとします。 このような時系列を
I.I.D (Indendent Identically Didtributed ) と呼んでいます。 帯域が 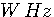 に制限されているとき、1秒間の時系列の長さの最大を に制限されているとき、1秒間の時系列の長さの最大を 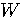 にすることができます。 各サンプル値を量子化して得られる中央値の列は、シンボルを出力する無記憶情報源から発生したとみなせるので、エントロピーは、 にすることができます。 各サンプル値を量子化して得られる中央値の列は、シンボルを出力する無記憶情報源から発生したとみなせるので、エントロピーは、
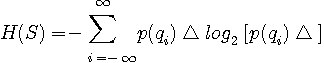
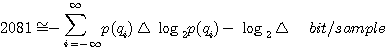
と書けます。 ここで、右辺第2項は
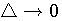 としたとき、無限大になってしまいます。 そこで、この項を次のように処理します。 としたとき、無限大になってしまいます。 そこで、この項を次のように処理します。
右辺第2項は量子化幅のみに依存し、信号には依存しない。
したがって、右辺第2項を無視して極限
 を計算する。 を計算する。
 を無限に小さくしたときのエントロピーは、 を無限に小さくしたときのエントロピーは、
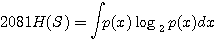
となります。 すなわち、これを、連続的な値をもつサンプル値系列
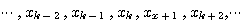
のエントロピーと定義します。
以下は、典型的なI.I.D系列のエントロピーです。
< 一様分布する無記憶アナログ情報源 >
シンボルを出力する無記憶情報源では、シンボルの頻度が同じとき、エントロピーは最大でした。 同様に、有限幅内にサンプル値が収まるならば、上の定義の文脈から、一様分布するとき(どの値も同じ確率で出現するとき)エントロピーが最大になるはずです。 すなわち、区間 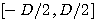 で一様分ならば、 で一様分ならば、
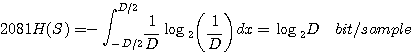
となり、単に区間幅  に依存します。 に依存します。
注1:  が大きくなるとエントロピーも大きくなりますが、 が大きくなるとエントロピーも大きくなりますが、 で で  になってしまいます。 次の例でも同じです。 これらのことは、連続分布をイメージすると、どう解釈してよいか判然としません。 この矛盾は量子化の項 になってしまいます。 次の例でも同じです。 これらのことは、連続分布をイメージすると、どう解釈してよいか判然としません。 この矛盾は量子化の項
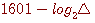 を無視したところで起こりました。 ただし、エントロピーの差 を無視したところで起こりました。 ただし、エントロピーの差
 を評価するとき、 を評価するとき、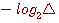 は打ち消しあうのでこの矛盾は解消します。 相互情報量あるいは通信路容量を扱う場合は、この項が打ち消しあうので、直感的な理解が可能になります。 は打ち消しあうのでこの矛盾は解消します。 相互情報量あるいは通信路容量を扱う場合は、この項が打ち消しあうので、直感的な理解が可能になります。
<正規分布する無記憶アナログ情報源>
正規分布(ガウス分布)は裾を無限に広げた形をしています。
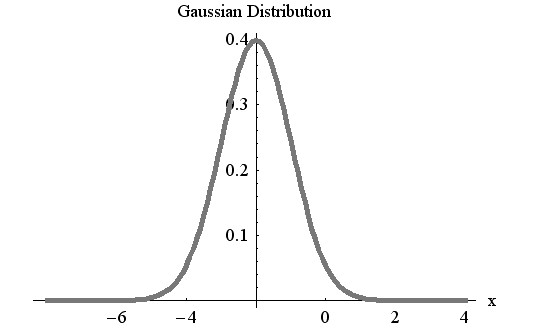
この分布は、いろんな分野で頻繁に登場します。 元のアナログ信号との間で標本化定理が満たされているとき、帯域制限されたガウス雑音のモデルとして計算機シミュレーションなどで広く用いられます。 実は、ガウス雑音は無限区間を前提にした確率分布関数の中で最大エントロピーを与えることがいえます。 すなわち、分散(アナログ信号の電力)が一定であるという拘束条件
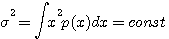
のもとで、エントロピーを最大化すると、正規分布(ガウス分布)
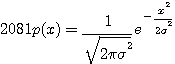
になります。 このときのエントロピーは
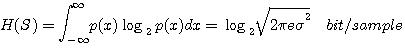
となり、分散 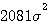 が大きい(信号の電力が大きい)ほどエントロピーは大きくなります。 が大きい(信号の電力が大きい)ほどエントロピーは大きくなります。
注2:一様分布と同様に、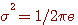 のときエントロピーがゼロになります。 のときエントロピーがゼロになります。
(B) マルコフ・アナログ情報源のエントロピー
実際にわれわれが扱う音声信号や画像信号は非常に強いマルコフ性をもっています。 このエントロピーは、シンボルを扱うマルコフ情報源のエントロピーを参照して、次のように導くことができます。 まず、マルコフ性がおよぶ範囲を無限過去までとると、正確な評価
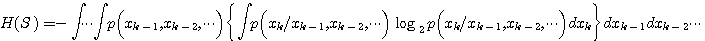
を得ます。 この式を計算することは実際には不可能ですから、近似式を求めます。 マルコフ性がおよぶ過去を 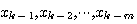 と仮定し、この系列をブロック と仮定し、この系列をブロック 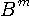 で表すと、ブロック長がm+1のエントロピーを次のように書くことができます。 で表すと、ブロック長がm+1のエントロピーを次のように書くことができます。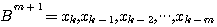 として、 として、
この結果は、シンボルを扱う情報源の場合と同じ表現です。ここで、  は長さmのブロックがその定常確率で無記憶に発生するとしたときの随伴情報源を意味します。 は長さmのブロックがその定常確率で無記憶に発生するとしたときの随伴情報源を意味します。
サンプル値系列を長さmで区切ってブロック化し、
各ブロックの頻度を計測して、随伴情報源のエントロピー を求める。 を求める。
ブロック長をm+1にして、同様に 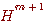 を求める。 を求める。
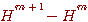 が前回の が前回の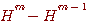 と大差がなければ止める。 と大差がなければ止める。
ハフマン符号で圧縮符号を求める。
|



 で表わし、区間の中央値
で表わし、区間の中央値