|
一般化相関シンボル伝送 THP (Tomlinson Harashima Precoder) |
|
伝送路が周波数減衰特性をもっている場合も、注水定理をOFDMやTHPによって実現できます。このページはTHPを解説します。 <注水定理: 簡単な例題> 有色ガウス雑音に加えて、チャンネルの減衰特性も存在するとき、注水定理は次のように拡張できます。 帯域を離散的に区分し、各区分の信号電力の減衰を
注1: もし、送信スペクトルの上限が制限されているならば、上限のフラットスペクトルを送信することが自明の解。THPはフラットスペクトルを送信する。 この様子を、次の簡単な例題で当たってみます。
として、
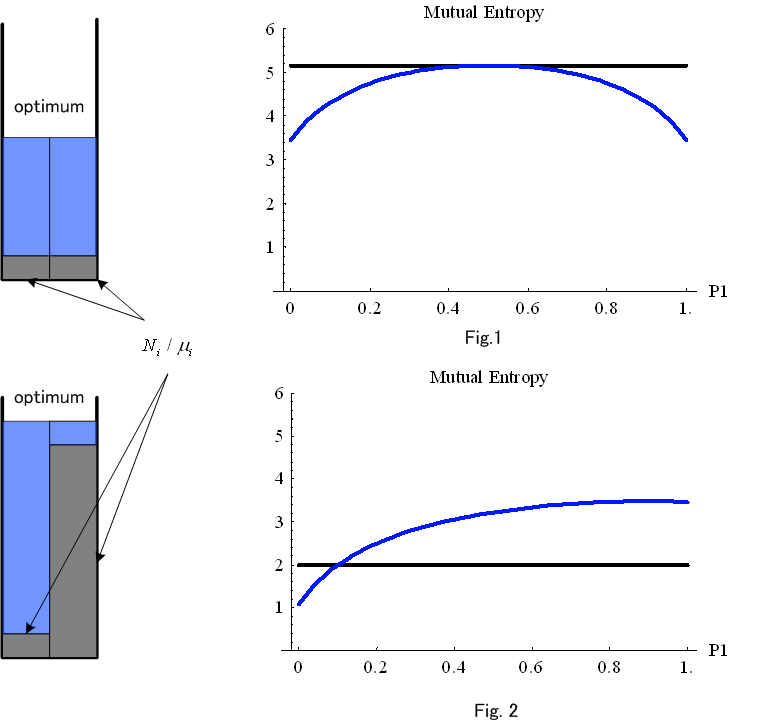
の2つのケースについて、送信電力
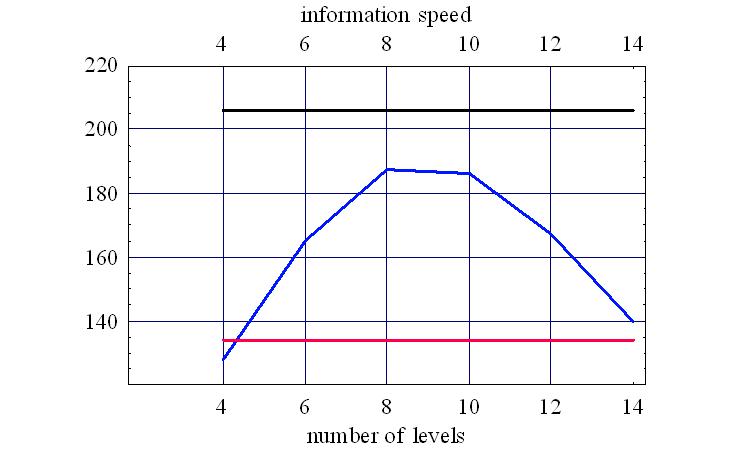
黒い直線は、二つの帯域をまとめた PAM (Pulse Amplitude Modulation) の情報伝送速度
をプロットしたものです。 Fig.1の青いカーブもFig.2の青いカーブも、頂上では非常にフラットであることが分かります。 また、減衰率が偏っている Fig.2 のケースでは、最適配分 (
<注水定理: 金属線伝送の例題> 次に、信号電力の減衰率が
白色雑音を仮定し、各区分の電力を 1/1000 としたときの
これに総電力
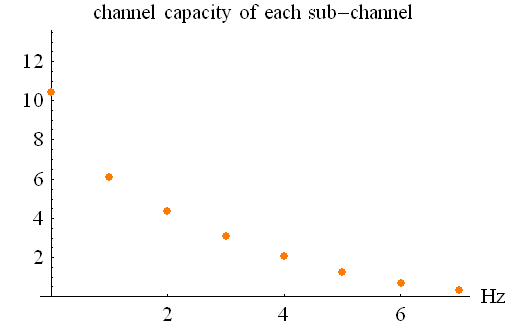
そして、このときの各区分の評価関数値(相互情報量)は下図のようになります。
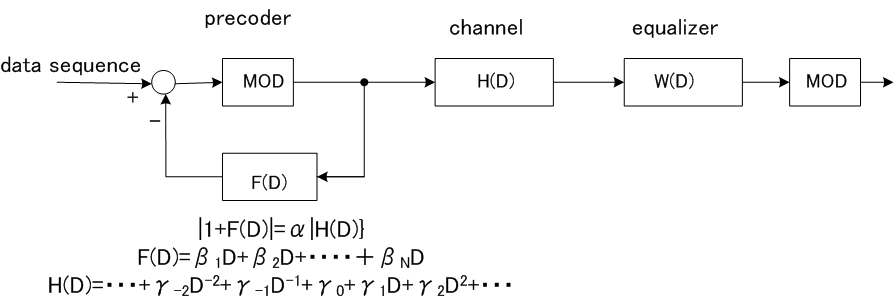
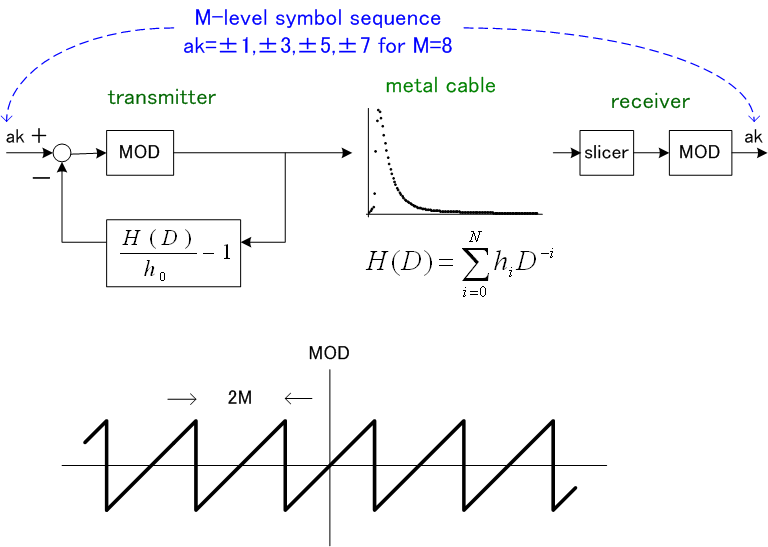
上のダイダイ色の総和は情報伝送速度の理論限界を与えます。 この注水結果と、信号電力を均等配分をした結果と、全帯域を使ったPAMの結果の3つを比較すると、下記のような情報伝送速度になり、やはり均等配分は最適に非常に近いことが言えます。 この場合も、PAMは大変劣っています。 情報伝送速度の理論限界=28.449 ビット/シンボル 以下、THPの実現例を2つ示しますが、いずれの場合も、フラットスペクトルの信号を送信しています。前記したように、フラットスペクトルの送信はスペクトルの上限が制限されたときの自明解であり、また、送信電力が制限された場合でも最適解にかなり近いことが言えます。このような理由から、THPはもっと評価されるべきではないかと思われます。 <THPの適用(1): メタルケーブル(最小位相位相推移チャンネル)のケース> まず、下図のプリコーダーと相関器は、任意の回路 F(D) に対して互いに逆システムになっています。
この逆システムの原理を利用したのがTHPであり、ブロック図は下のようです。 つまり、チャンネル応答をそのまま相関器にしてしまうという発想です。
上の図から、以下のことが読み取れます。
というわけで、先ず、実際の金属線の超高速伝送(1Gbit/sec以上)について、THP方式のコンピュータ・シミュレーションを実行した結果を示します。次に、マルチパスのような非最小位相推移チャンネルの場合への応用例を示します。
8値シンボルの場合
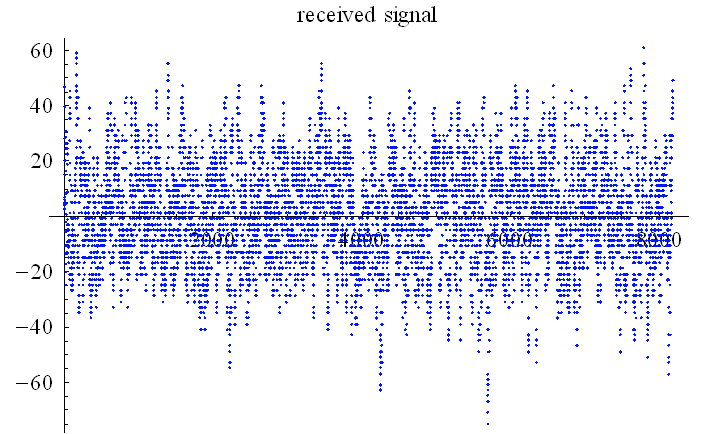
8値シンボルの場合 (受信信号のレベル数が60以上になっているが、
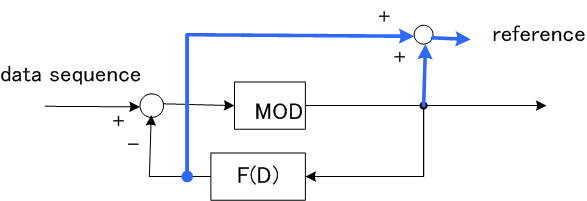
青色のカーブはTHPの情報伝送速度であり、8値シンボル伝送において最大になっています。 黒い直線はアナログ情報源で計算した通信路容量です。 赤い直線は8値PAMの情報伝送速度を表します。レベル数が8のとき黒色に近いとは言え、インパルス応答の先頭値が小さいため、レベル数が多くなって良い応用例とは言えません。 <THPの適用(2): 一般的な(非最小位相推移チャンネルの)ケース> 上記のストーリーは、チャンネル応答が最小位相推移で、かつ、 一般化のブロック図を下のようになります。1+F(D) の振幅特性を伝送路 H(D) の振幅特性の定数倍に等しくします。このとき、F(D) には位相の自由度が残っているので、この自由度を使ってF(D)が急減少応答であるように設計できれば、送信シンボルのレベル数を減少できます。チャンネルの位相特性と 1+F(D) の位相特性の和は受信側の等化器で吸収します。
なお、等化器は送信相関系列(下のブロック図の青色で出力される referenceで離散値レベルをもつ)を出力するように強制等化します。この結果、等化器は位相特性だけを等化することになり、振幅特性はフラットなので、雑音の増幅はありません。
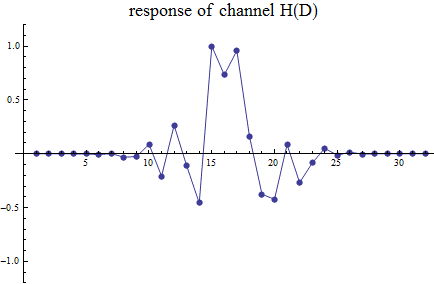
ここで、1+F(D) の設計が重要なテーマです。それは一義的に決まるものではないが、理論的にスッキリする例として、H(D) が因果的な最小位相推移FIRと反因果的な(時間の逆方向に向かって因果的な)最小位相推移FIRに分解するアイデアが考えられます。こようなH(D) の分解については、因果律、逆システム、最小位相推移、線形予測などのページと関連します。 以下、例題をシミュレーションした結果をグラフで示し、説明を加えます。 乱数を用いて発生した非最小位相推移なチャンネル応答
このチャンネルにランダム信号を入力したときの出力信号に対して
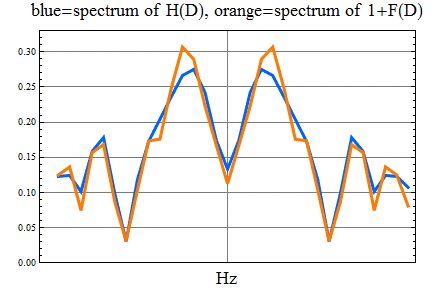
青色はチャンネルの振幅特性、オレンジ色は1+F(D) の振幅特性
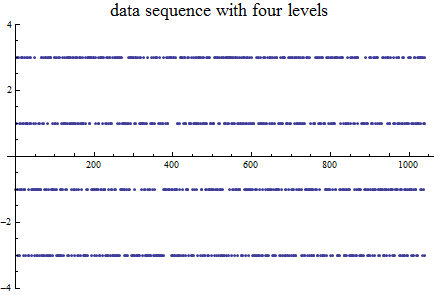
4値送信データ系列
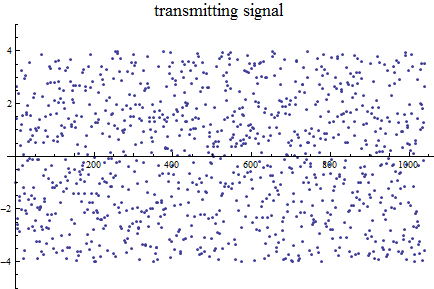
送信信号(MOD計算の結果)はこのように一様分布するランダム系列になる。
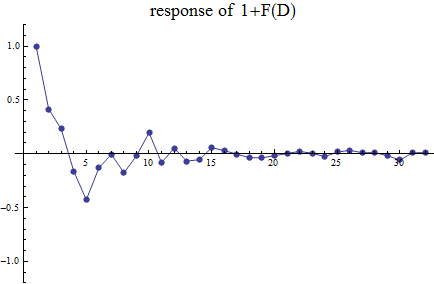
このランダム信号を1+F(D) に通すと下のように相関を持った
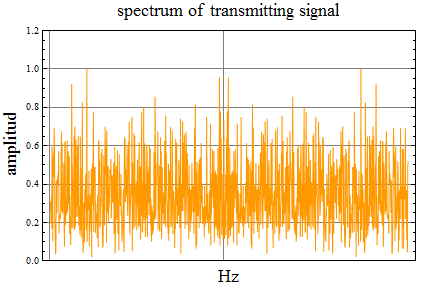
前記の一様分布するランダム送信信号のスペクトル。
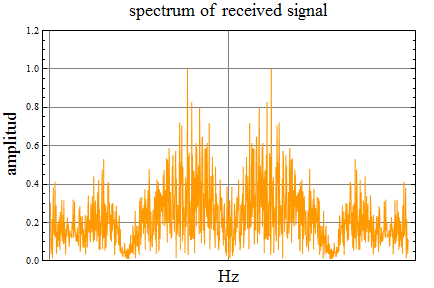
受信信号のスペクトル
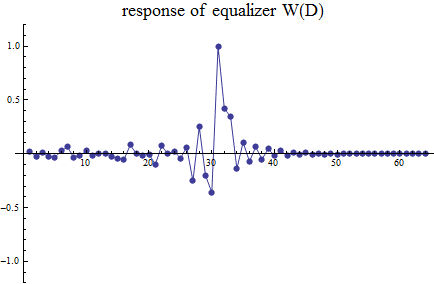
等化器のタップ重み
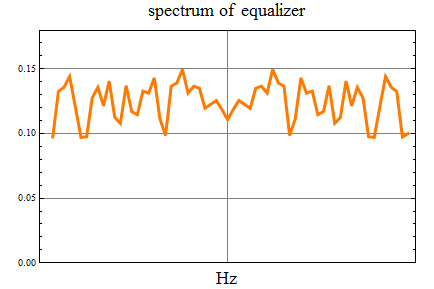
等化器の周波数特性。ほぼ平坦になっている。
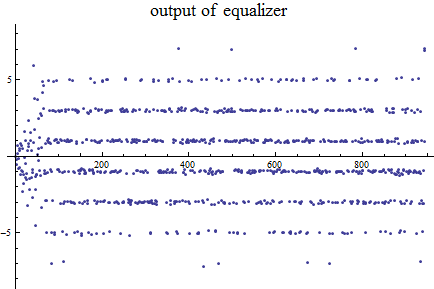
等化器の出力。チャンネルの振幅特性が大きく暴れているので、
注2: 1+F(D) は受信側で求め、それを送信側に送ります。送信側は、precoderにF(D) をセットしてデータを送るだけです。 注3: 雑音が非常に大きいとき、モデムはフォールバックする必要があります。この対応は、単に送信シンボルの速度を1/2,1/4,・・・・のように落とせば済みます。例えば、1/2に速度を落とすと、シンボルの電力を2倍にすることができます。更に、1+F(D) は一つおきに間引きサンプルしたものとなり、この結果、ブロック図のreference信号のレベル数が下がります。このように、フォールバックが自動的に遂行されます。OFDMのフォールバックは、サブチャンネルへのビット配分やブロック再組立てなど、やっかいな処理が必要になります。 |
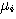 で表す。
で表す。 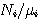 を雑音電力とみなせば、注水の評価関数は下式のようになる。
を雑音電力とみなせば、注水の評価関数は下式のようになる。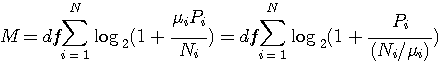
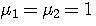 と
と 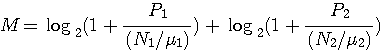
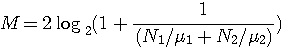
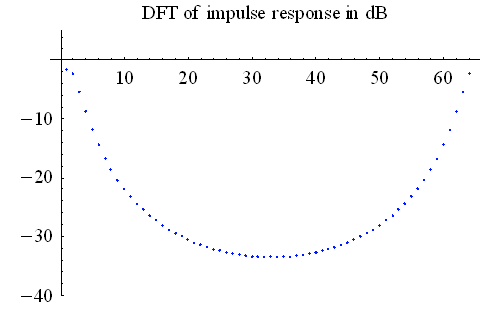
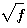 dB のカーブになる金属線伝送を想定してみましょう。AWGNを仮定し、8個の帯域に分割して、減衰(≦1)を下図のようにしてみます(縦軸は
dB のカーブになる金属線伝送を想定してみましょう。AWGNを仮定し、8個の帯域に分割して、減衰(≦1)を下図のようにしてみます(縦軸は 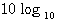 減衰)。 帯域の右端をナイキスト周波数(シンボルレート/2)とすると、ー30dBとなり、かなり厳しい高速伝送モデルといえます。
減衰)。 帯域の右端をナイキスト周波数(シンボルレート/2)とすると、ー30dBとなり、かなり厳しい高速伝送モデルといえます。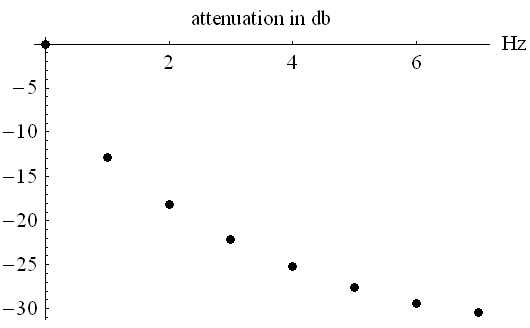
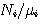 は下のようになります。
は下のようになります。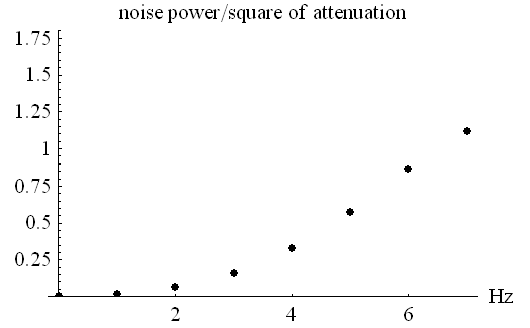
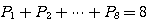 を注水すると、下の青色のような最適配分になります。
を注水すると、下の青色のような最適配分になります。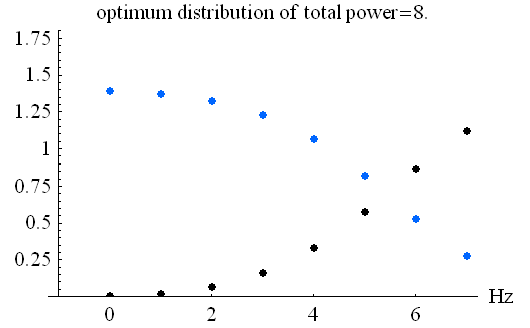
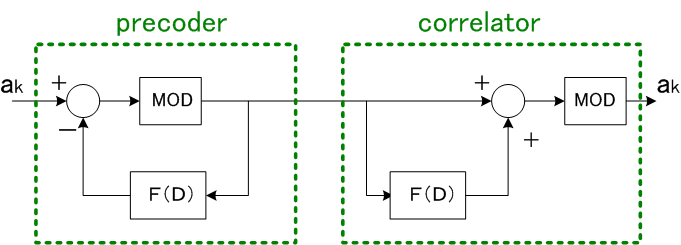
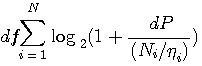
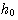 が小さいと、プリコーダーの帰還信号が大きくなり、レベル数が多くなる。
が小さいと、プリコーダーの帰還信号が大きくなり、レベル数が多くなる。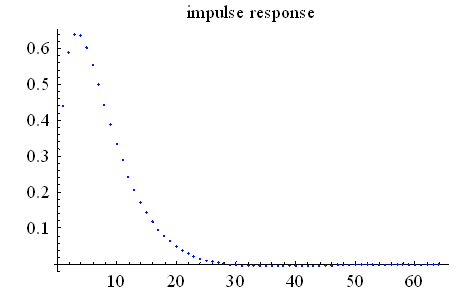

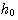 が大きいケースであり、現実的ではありません。一般の応用では、チャンネル応答は非最小位相推移なので、THPをこの場合へ一般化します。
が大きいケースであり、現実的ではありません。一般の応用では、チャンネル応答は非最小位相推移なので、THPをこの場合へ一般化します。