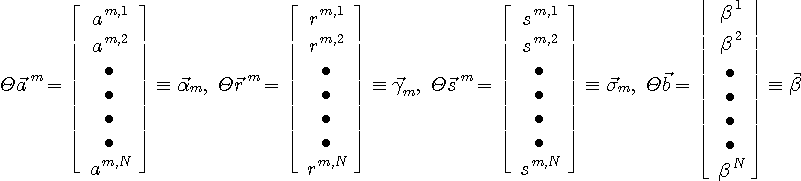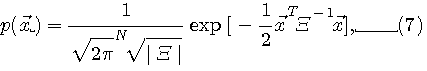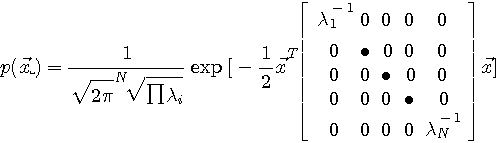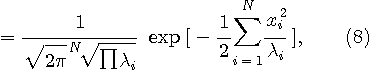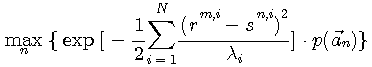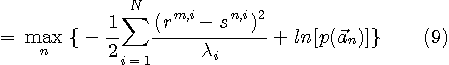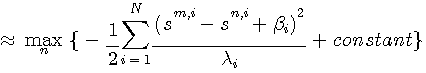|
最尤系列推定では雑音をAWGNとし、受信フィルターを置かないシンプルなケースを対象にしましたが、ここでは一般的な伝送システムを前提とします。
雑音 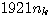 は加法的(有色)ガウスとします。 受信フィルタ は加法的(有色)ガウスとします。 受信フィルタ 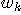 は、雑音モデル仮定して、整合フィルタ(case
of Ungerboeck)や白色化フィルタ(case of Forny)などを置くのが常套的ですが、ここでは任意として事後確率を最大にする判定法のアウトラインを説明します。 は、雑音モデル仮定して、整合フィルタ(case
of Ungerboeck)や白色化フィルタ(case of Forny)などを置くのが常套的ですが、ここでは任意として事後確率を最大にする判定法のアウトラインを説明します。
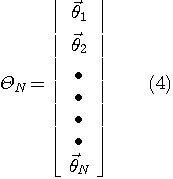
受信フィルタの出力のサンプル値、
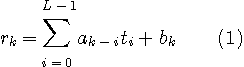
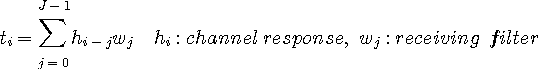
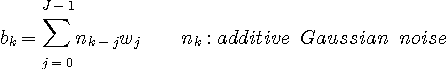
の十分長い有限区間  をとって、このベクトルを をとって、このベクトルを  で表します。 判定は事後確率 で表します。 判定は事後確率
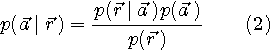
を最大にする送信シンボルベクトル系列  を選択することになります。 この判定で、分母は共通なので省くことができ、結局、 を選択することになります。 この判定で、分母は共通なので省くことができ、結局、

を求める問題になります。 もし、 が等確率ならば、結果 が等確率ならば、結果  を固定して、条件付確率 を固定して、条件付確率 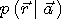 を最大とする原因 を最大とする原因  を見つける最尤系列推定になります。 MAPでもMLSEも、 を見つける最尤系列推定になります。 MAPでもMLSEも、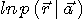 が簡単な形で表されることが必要ですが、冒頭の一般モデルについて導いてみましょう。 方針として、雑音に対する
Karhunen-Loeve expansion を用いて、直交基底の上で独立に信号を扱えるようにします。 が簡単な形で表されることが必要ですが、冒頭の一般モデルについて導いてみましょう。 方針として、雑音に対する
Karhunen-Loeve expansion を用いて、直交基底の上で独立に信号を扱えるようにします。
注1:Karhunen-Loeve
展開の代わりに、フーリエ直交展開を用いても以下を近似的に実行できます。 Nが十分大きいときは、両者はほとんど同じ結果になります。
雑音
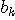 の自己相関が分かっているとし、これを の自己相関が分かっているとし、これを 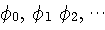 とし、N次元の自己相関行列を とし、N次元の自己相関行列を 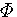 で表します。 この行列の固有値と固有ベクトルを で表します。 この行列の固有値と固有ベクトルを 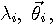 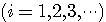 とします。 これは雑音 とします。 これは雑音 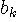 に対する Karhunen-Loeve 展開です。 固有ベクトルを行とする正規直交行列 に対する Karhunen-Loeve 展開です。 固有ベクトルを行とする正規直交行列
で信号を直交変換していきます。 式(1)の右辺第1項を
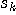 で表し、信号ベクトルを次のように表します。 右肩の m は、m 番目の信号系列パターンを意味しています(仮に、 で表し、信号ベクトルを次のように表します。 右肩の m は、m 番目の信号系列パターンを意味しています(仮に、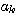 を2値とすると、パターンの総数は を2値とすると、パターンの総数は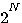 個)。
以下、記述の簡単のため、信号や雑音の期待値をゼロと仮定します。 個)。
以下、記述の簡単のため、信号や雑音の期待値をゼロと仮定します。
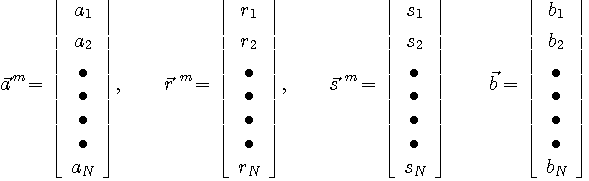
ここではチャンネル応答と受信フィルタを既知としており、これらを用いて、 は送信データの候補 は送信データの候補  から作るものとします。上のベクトルを直交変換した結果を次のように記します。 から作るものとします。上のベクトルを直交変換した結果を次のように記します。
ここで、 は雑音に起因する確率変数で、固有ベクトル は雑音に起因する確率変数で、固有ベクトル 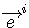 の確率的変動を表しています。 の確率的変動を表しています。 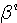 は無相関になっており、自乗の期待値は固有値を与えています(Karhunen-Loeve expansionを参照)。 さらに、ガウス雑音の前提から、 は無相関になっており、自乗の期待値は固有値を与えています(Karhunen-Loeve expansionを参照)。 さらに、ガウス雑音の前提から、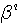 もガウス分布に従います。 つまり、 もガウス分布に従います。 つまり、
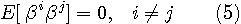
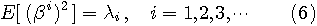
したがって、ベクトル 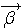 の確率密度関数は次のようになります。 の確率密度関数は次のようになります。
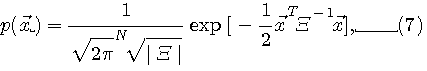

 は式(5)と(6)から は式(5)と(6)から  (正値に関しては自己相関行列を参照)を要素とする対角行列なので、 (正値に関しては自己相関行列を参照)を要素とする対角行列なので、
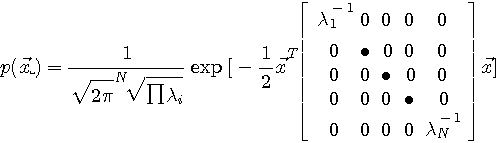
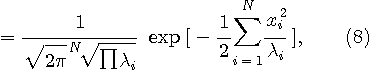
となり、最大事後確率判定が次のように得られます。 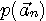 はn番目の送信シンボル系列の生起確率を示しています。 はn番目の送信シンボル系列の生起確率を示しています。
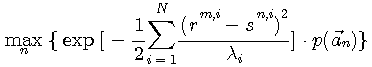
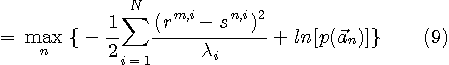
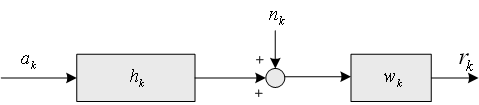
この判定は下のように図解できます。
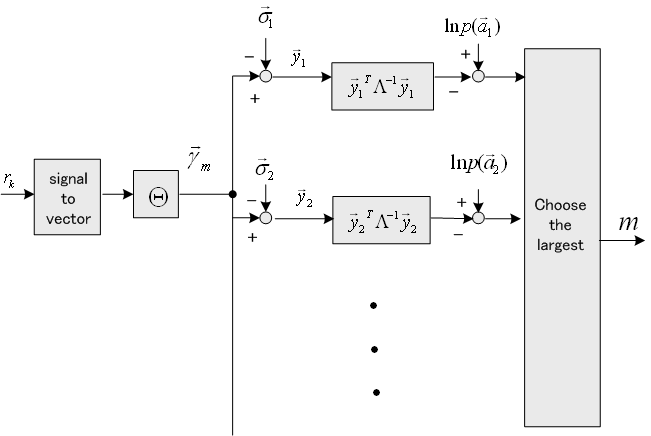
自己相関行列で説明したように、Nが十分大きい場合には、固有値
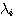 は雑音の電力スペクトルのサンプル値を近似しています。 また、式(9)の は雑音の電力スペクトルのサンプル値を近似しています。 また、式(9)の 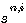 は受信信号系列 は受信信号系列 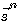 を を  で正規直交変換したベクトルの要素ですが、 で正規直交変換したベクトルの要素ですが、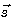 空間から 空間から 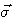 空間への変換はベクトル間距離を保っています。 空間への変換はベクトル間距離を保っています。
特別な場合として、送信シンボルを独立、受信フィルターを整合フィルタ
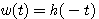 、雑音を白色 と仮定してみます。 式(9)を分解してみましょう。 、雑音を白色 と仮定してみます。 式(9)を分解してみましょう。
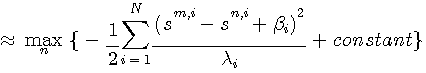
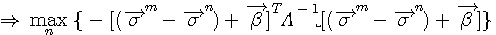
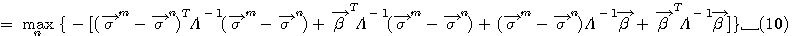
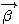 は雑音が整合フィルターを通過した信号ベクトルを は雑音が整合フィルターを通過した信号ベクトルを 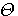 で変換した結果であり、i 番目の要素の二乗平均が固有値 で変換した結果であり、i 番目の要素の二乗平均が固有値 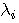 でした。 一方、 でした。 一方、  はランダムデータがチャンネルと整合フィルタの二つを通過した信号ベクトルを はランダムデータがチャンネルと整合フィルタの二つを通過した信号ベクトルを  で変換した結果ですが、i 番目の要素の二乗平均は で変換した結果ですが、i 番目の要素の二乗平均は 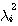 になります(自己相関行列に例題あり)。 になります(自己相関行列に例題あり)。 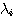 がチャンネルの(整合フィルターの)電力スペクトルであることから、[ ]内の項の物理的意味を次のようにまとめることができます。 がチャンネルの(整合フィルターの)電力スペクトルであることから、[ ]内の項の物理的意味を次のようにまとめることができます。
第1項は、候補データと源送信データの信号間距離を、周波数領域において 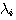 で重み付けしたものである。信号が通りやすい帯域を強調して信号間距離を評価している。 第2項と第3項は雑音と上記信号間距離のクロスタームであるが、周波数領域において、 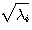 で重み付けしたものであるが、期待値はゼロである。 第4項は源雑音 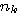 の電力であり、正のバイアスである。
|



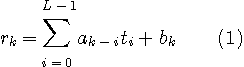
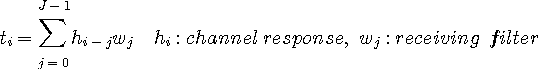
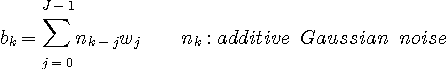
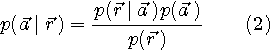
 を見つける最尤系列推定になります。 MAPでもMLSEも、
を見つける最尤系列推定になります。 MAPでもMLSEも、