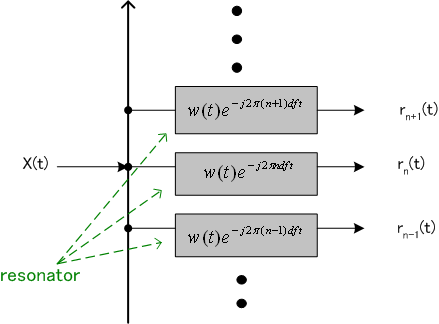
信号 x(t) の周波数分析（短時間フーリエ変換）を離散的に実現したものは下図のようでした。

周波数きざみ df で並べられた共振器の出力、・・・, r_n-1(t), r_n(t), r_n+1(t),・・・ が x(t) に含まれるそれぞれの周波数成分でした。　電力スペクトルは、これらの周波数成分の電力（自乗平均）をプロットしたもです。　この概念にそって、

定理 （ Wiener-Khintchine ）
 電力スペクトルのフーリエ逆変換は信号 x(t) の自己相関に等しい

を導いてみましょう。　

その前に、x(t) は初等関数で表されるような確定した信号ではなく、確率過程（この場合はエルゴード的で定常）であることを前提にします。　分析すべき信号 x(t) は一つの実現したサンプルですが、それが一定の確率的ルールによって生み出されたものと考えるのです。　

では、具体的に周波数分析

から電力スペクトルを求め、そのフーリエ逆変換を計算してみましょう。　電力スペクトルは

で与えられますが、右辺をもう少し変形すると次のようになります。

ここで、 は x(t) の自己相関です。　次に、これをフーリエ逆変換します。

ここで、｛　｝内がデルタ関数 になるので、

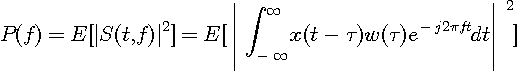
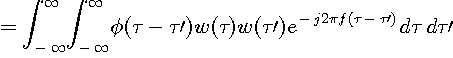
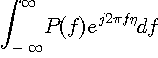
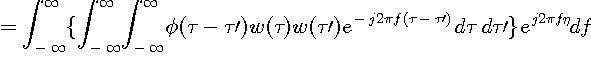
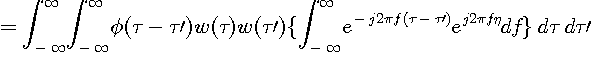
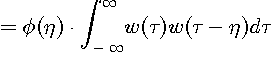
が得られます。　このようにして、周波数分析（短時間フーリエ変換）の電力スペクトルから、自己相関の近似が得られることが分かりました。　上の形は、自己相関を包絡線 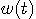のコンボリューションを通して見ていることを意味しており、それが自己相関が集中する範囲でフラットならば、小さい歪みで自己相関が観測されることがわかります。