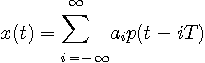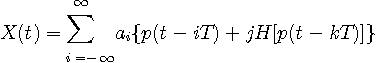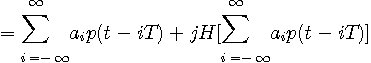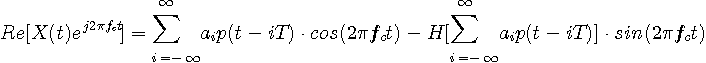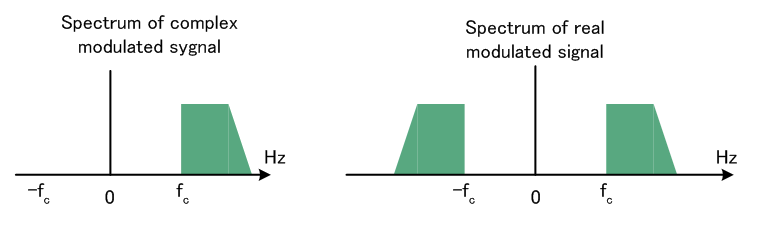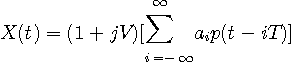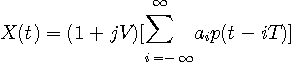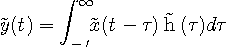チャンネル歪が送信ベースバンド信号に対して線形の関係で加わるような変調方式を線形変調と総称しています。　線形性を満たさない代表的なものは周波数変調です。　線形性とは、二つの任意の送信ベースバンド信号 と が歪んで と になったとき、 の受信信号が になることです。　この線形性を前提として、等化や系列推定といったチャンネル歪を除く処理が施され、高速ディジタル通信が実現されています。　したがって、ほとんどの高速ディジタル通信では線形変調を採用しています。　線形変調は次の４つに分類されます。　ディジタル通信で実用されている多くはQAMです。

とします。　この信号は実数値であり、パルス は余弦ロールオフスペクトルをもつナイキストパルスを使うのが普通です。　
まず、シンボル系列がランダムであり、ほとんどのディジタル通信がそうであるように、

を仮定します。　 は期待値を表しています。　たとえば、スクランブルされた２値信号 は上の条件を満たします。　これが満たされていると、パルス のフーリェ変換を としたとき、送信ベースバンド信号の電力スペクトルは で与えられます。　BSBAMはこのベースバンド信号に搬送波 を掛けるだけで済みます。　変調波は

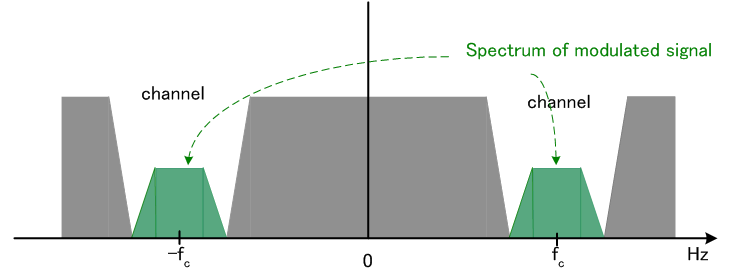
ですが、この変調波の電力スペクトルは、

のようになり、ベースバンド信号の電力スペクトル を搬送波周波数 と の位置まで平行移動したものになっています。　したがって、パルス波形が正確に帯域制限されていれば、下図のように信号エネルギーを決められた周波数帯域（チャンネル）の中に押し込めて伝送することができます。

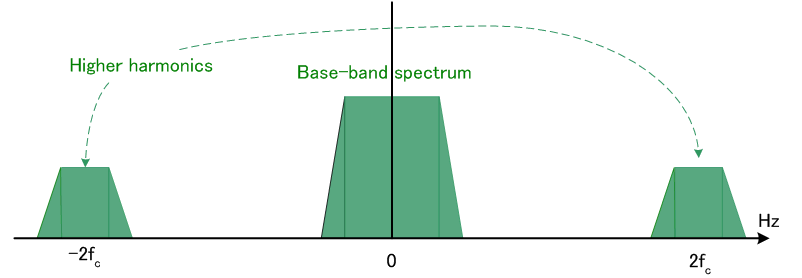
復調は、変調波に再び搬送波を同じ位相で掛けます。　結果は

となり、第１項が所望のベースバンド信号、第２項は不要な高調波成分です。　高調波成分は　　という高い周波数に分離したので、簡単な低域通過濾波器(Low Pass Filter )で除去することができます。

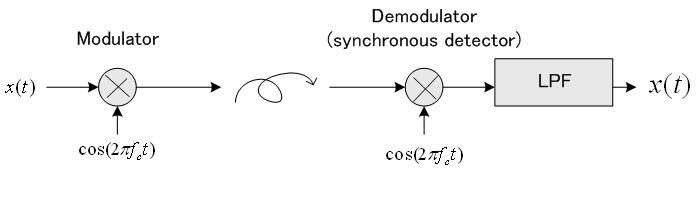
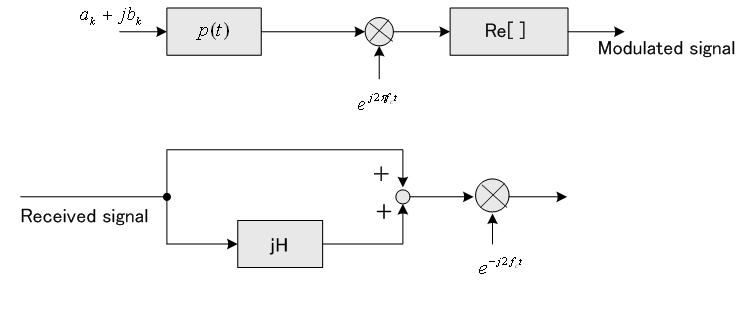
変調と復調のブロック図を下に示します。　下のような復調法を同期検波と呼んでいます。

以上はあくまでも理想的な原理であることに注意してください。　たとえば、復調器の中で作られる搬送波は送信搬送波と正確に同期して掛け算されています。　現実には、いくら正確な水晶発信器でも変調側と復調側の搬送波が同じ周波数ということはあり得ません。　実際の受信機では、同期検波によって受信側の再生搬送波を同期（周波数も位相も一致）させています。ただし、われわれがいつも聞いているAMラジオはBSBAMですが、それは同期検波を必要としない方式です。　鉱石ラジオを作った人ならば、上のような掛け算回路を使わなかったことを思い出すでしょう。　同期検波を避けて手軽に回路を製作できるように考案された一種のBSBAMです。　ただし、信号対雑音比を犠牲にするのでディジタル通信には向いていません。

B:：　単側波帯振幅変調　(SSBAM = Single Side Band Amplitude Modulation)
上のBSBAMで用いたパルス は実数値でした。　実数のパルスのスペクトルは次のように複素共役対称になっています。

右肩の＊は複素共役を表しています。　このスペクトルを平行移動してチャンネルにすっぽりはめ込んだわけですが、考えてみると正側（の部分）が決まれば負側（の部分）はその複素共役なので無駄ですね。　そこで、このスペクトルの負側をカットします。　このような操作は、ヒルベルト変換を用いて実現できます。　ヒルベルト変換を で表します。　信号に を作用させると負側のスペクトルがカットされ、 を作用させると正側がカットされます。　こうして作った複素パルス

を用いて実シンボル を送ります。

が複素ベースバンド信号です。　また、ヒルベルト変換は線形操作なので、上の式は

のように展開することができます。　SSBAMは、このベースバンド信号に複素搬送波 を掛け算し、その実部を選択して送ります。　すなわち、

が実際に送信される変調波です。　複素変調波 と、実際に送信する実変調波 のスペクトルを下に示します。

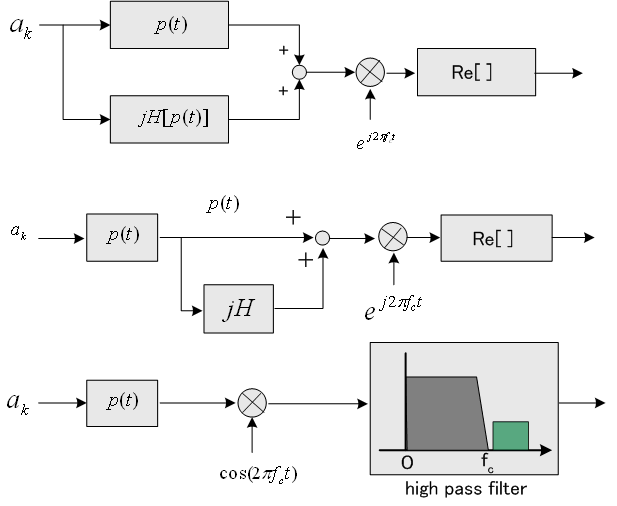
実変調波の作り方は３通りあります。

これらに対応するブロック図を下に示します。

以上のように、実ベースバンド信号をちょうど半分の帯域にしました。　もし、この変調信号はから実ベースバンド信号を復調できれば、BSBAMは半分の帯域を無駄遣いしていたことになります。

復調は、まず受信変調波の負周波数成分をカットし、正周波数成分を選択します。　このことは  に受信信号 を入力して実現できます。　出力は

となります。　この操作は９０度位相差分波器という高周波アナログ回路で実現できます。　変調波は非常に高い周波数帯に位置しているので、この高周波回路は比較的簡単に実現できます。　もちろん、適当な中間周波数（IF)に落としてディジタルフィルターで実現することも可能です。　この出力に複素搬送波の逆回転 を掛ければ複素ベースバンド信号 が得られます。　そして、この実部が所望のベースバンド信号です。　この復調方式も、再生搬送波が受信搬送波にぴったり同期していることが必要なので、同期検波です。　SSBAMでは、同期検波の制御が非常に困難なので、別にパイロット・トーンを送り、これから周波数がぴったり合った搬送波を作り出します。　復調のブロック図を下に示します。

C：　残留側波帯振幅変調　(VSBAM = Vestigial Side Band Amplitude Modulation)
理想的なヒルベルト変換は、直流で不連続な特性をもっています。　このような不連続性を正確に実現するのは困難です。　そこで、この不連続性をなだらかなカーブで近似して、矛盾なく復調できるようにしたのが残留側波帯振幅変調です。
ヒルベルト変換は、すべての周波数成分を大きさを変えずに通過させ、正周波数成分は位相を９０度ずらせ、負周波数成分は位相をー９０度ずらせる操作を実現するものです。　この不連続な位相特性を原点対称の曲線で滑らかにし、さらに適当に帯域制限をかけたものを考えます。　この擬似ヒルベルト変換を で表します。　下図は、振幅を余弦ロールオフ（水色）、位相ジャンプを正弦関数（ピンク色）とした場合の周波数特性と、そのインパルス応答です。　ただし、ヒルベルト変換の数学的な定義は

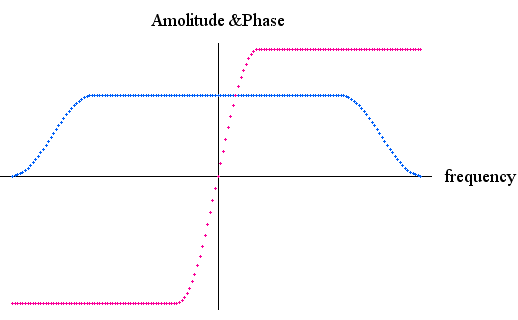
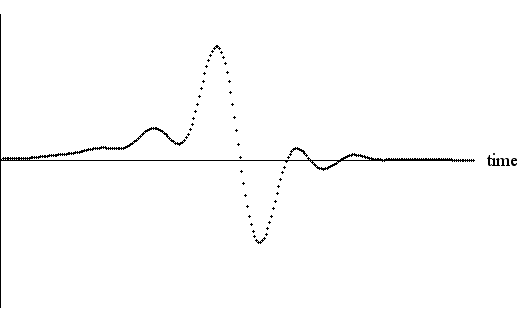
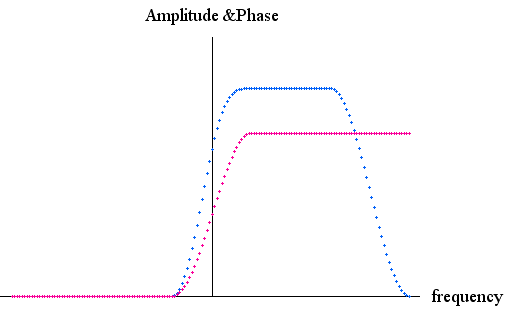
これを使って片側スペクトルを滑らかにカットする特性は、いままでの議論のように無限に周波数が伸びていれば の表現でいいですが、ディジタルフィルターで実現する場合は （ロールオフFIR + ）とします。　特性は下のようになります。 水色が振幅特性、ピンク色が位相特性で正周波数領域のフラットな部分は radian です。

送信すべき複素ベースバンド信号は

変調波は

です。　復調はSSBAMと同じように実行します。　９０度位相差分波器によって変調波の正周波数成分を選択するところはSSBAMとまったく同じでよいことに注意してください。　計算過程は省きますが、復調結果として、再び

が得られ、実部を選択すれば所望の実ベースバンド信号が得られます。　VSBAMにおいても、同期検波の困難さは残ります。　やはり、普通はトーン信号を別送りして解決しています。

D：　直交振幅変調  (QAM = Quadrature Amplitude Modulation)
SSBAMもVSBAMも、BSBAMの帯域の半分を節約する方式でしたが、QAMはBSBAMと同じ帯域を使って、二つの独立なシンボル系列 と を同時に伝送します｡　現在のほとんどのディジタル通信はQAM方式を採用しています。　複素信号を用いて変調と復調のプロセスを描くと下のようになります。

同期検波に関してはやはり難しい問題が残りますが、SSBAMやVSBAMと違い体系的な扱いが可能です。　ただし、同期検波は本質的にブラインドパラメータ推定なので、その困難さは最後まで残ります。

E：　振幅変調の統一的表現
上記４つの振幅変調の変調波を以下のように統一表現できます。

Ｆ：　チャンネル歪の加わり方
振幅変調は線形変調です。　すなわち、パルスの線形歪(有線ならば線路の周波数特性の歪や各種フィルターの歪、無線ならばマルチパス）が送信ベースバンド信号に対して線形に加わります。　このことは、チャンネル歪を取り除く等化器を実現することができ、高速ディジタル通信を可能にします。　チャンネルは一種の帯域通過フィルターです。　非線形歪は大出力増幅などによって起こります。　通常は線形歪を仮定しますが、このとき送信ベースバンド信号と復調ベースバンド信号の間には線形関係が成立します。　その内容を具体的にみてみましょう。
搬送波周波数を中心にチャンネルが設定されていますが、そのインパルス応答を

で表します。　ここで大文字は複素数を表します。　このチャンネルを変調波が通過した結果は下のコンボリューションです。

この中に含まれるすべての信号は搬送波周波数を中心に高い周波数成分をもちますから、両辺を９０度位相差分波器に通せば、複素信号表現

が得られます。　 とおいて、さらに計算を続けると、

となります。　結局、同期検波によって検波されるベースバンド信号が

のように得られました.。

SSBAMやVSBAMでは、搬送波周波数はチャンネルの端の方に設定され、BSBAMやQAMでは、ほぼ真中に設定されます。　 は搬送波周波数を直流（ゼロHz）とみなしたときのチャンネルの等価ベースバンド応答であり、通常は複素数です。　もし、チャンネルが無歪であれば（信号の通過域で振幅特性が平坦で位相特性が直線）であれば、変調信号はそのまま通過するので、 を意味します。

G：　同期検波との関連
送信側の搬送波と受信機が作る搬送波が、周波数も位相もぴったり一致することが同期検波の理想的な目的です。　しかし、このようなことは先見的に実現できませんから、実際には受信側の再生搬送波の周波数と位相を制御する必要があります。　搬送波の周波数や位相の再生は等化器（あるいは最尤（さいゆう）系列推定）と密接に関係しています。　受信信号は最初に同期検波器に入力されますから、ここでの不完全さは以下に続く等化器（または最尤系列推定）などのシンボル判定の設計に大きな影響を及ぼします。　受信信号から搬送波の周波数を正確に再生する問題は大変難しい内容を含んでいます。　チャンネル歪が大きいと、搬送波の周波数を推定できないし、搬送波周波数が分からないと等化できないというディレンマに陥ります。　チャンネル歪が無視できないとして、概略は次のようにまとめることができます。　詳しくは同期検波を参照してください。

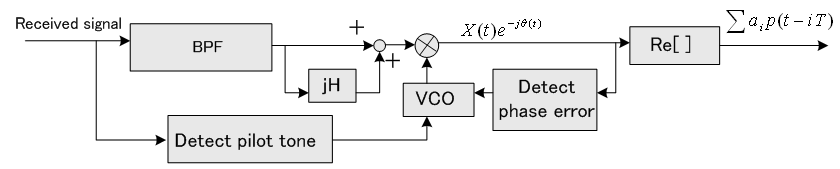
変調方式の議論をする場合、等化器あるいはそのブラインドモードのしっかりした知識を持たないと誤った結論に到達してしまいます。　とりあえず、パイロット・トーンなしで、なにも制御しない固定発信器で同期検波した場合、どのような問題が発生するかについて整理してみましょう。　このとき、同期検波後では、まだ大きな周波数誤差が残っていることに注意してください。

 

非常に過酷な条件下、すなわち、シンボルの多値数が大きく、チャンネル歪が大きく非対称で、搬送波周波数のオフセットが大きいとき、次のような復調スキームが上の表から読み取れます。　この他にも、良いアイデアがあると思いますが、参考にしてみてください。

（１）　ＱＡＭでは多相多レベルシンボル配置を前提とし、

（２)　ＶＳＢＡＭではパイロット・トーン方式を前提とし、

　　　　ただし、同期検波は等化器と共通制御になります。