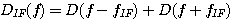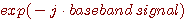|
周波数変調 Frequency modulation |
|
搬送波の周波数を変化させて情報を送る変調を周波数変調 (Frequency
Modulation) といいます。 チャンネルの中心周波数
と書きたくなります。 このような操作は VCO (Voltage Control Oscillator) によって周波数を変化させれば実現できるという理解もスムーズです。 では、この信号から送信ベースバンド信号
まず純粋に数学的に考えれば、余弦関数の逆関数をかけて
それでは、受信信号を微分してみましょう。 結果は
です。 一般に、中心周波数は非常に大きいので、送信ベースバンド信号の情報は高い周波数の変調波の包絡線の変化に含まれていることがいえます。 これならば、ダイオードで半波整流して、低域通過炉波器を通して包絡線を取り出すことができます。 取り出した後に、直流成分をカットすれば、
が得られます。
この出力から 冒頭の変調式を見直してみます。 問題は周波数という概念にありそうです。 上のストーリーで、暗黙のうちに
もしそうならば, 冒頭の変調式を
としてみましょう。 そして、上と同じように、微分して、整流して、直流カットすると、今度は
「VCOは周波数を変化させる回路」ではなく、 このようなことは、複素信号で考えると分かりやすいので、ちょっと繰り返しておきます。
実際には中心周波数
上で述べた 微分
のような回路が想定されます。 A点の出力を実部、B点の出力を虚部とみれば、この複素信号は単位円を角速度
のような回路が想定されます。 デスクリミネーターは中間周波数での微分を意味しています。 最後に、ベースバンドでの微分および中間周波数での微分について考えましょう。 詳しいことは微分というページを参照してください。 微分は信号の線形変換なので、その周波数特性が一意的に決まるはずです。 信号
ですが、右辺第一項はどう扱っていいかわかりませんね。 フーリェ変換は有限エネルギーをもつ信号しか扱えませんので、ここでは信号
となるので、微分の周波数特性は
のようになります。 青色の振幅特性は周波数に比例して大きくなり、赤色の位相特性は直流でジャンプしています。 このような特性は物理的に実現できません。 実際には、上の二つのブロック図において、A点、B点、C点でAD変換して、微分を差分で近似します。 サンプリング周期を
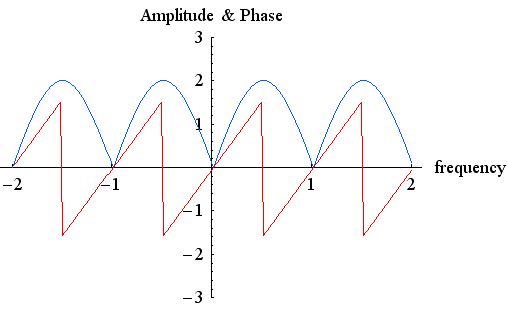
のようになり、直流の近くで微分を近似しています。 次に、デスクリミネーターの特性を見てみましょう。 微分特性
は、なにがなんだか分かりません。 この場合も、図2のC点でAD変換するのが普通です。 IF周波数によっては、AD変換のサンプリング速度は非常に高くなりますが、最近の技術では十分可能な実現法です。 直接、AD変換の出力に対して差分をとることも考えられますが、量子化誤差などを考慮するとあまりいい方法とはいえません。 そこで、下図のような特性を近似する帯域通過ディジタルフィルターを用います。 サンプリング周波数はIF周波数の数倍を必要とします。
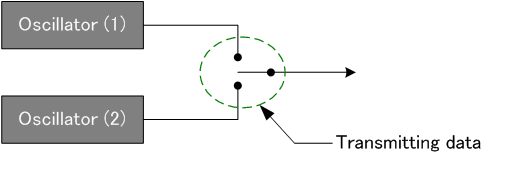
今までは、VCOによる変調方式について考えてきましたが、他にも方法があります。 下図のように、二つの発信器をもち、それを切り替える方法です。 切り替えは、瞬間的にスイッチで切り替えても、徐々に切り替えてもかまいません。 下図はスイッチで切り替える概念図を示しています。 VCO方式と違う点は、この方法では、位相が連続 (coherent) していることです。
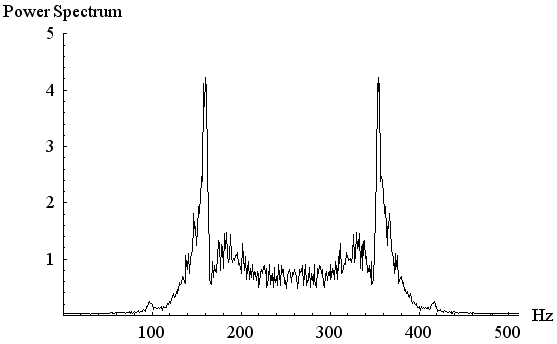
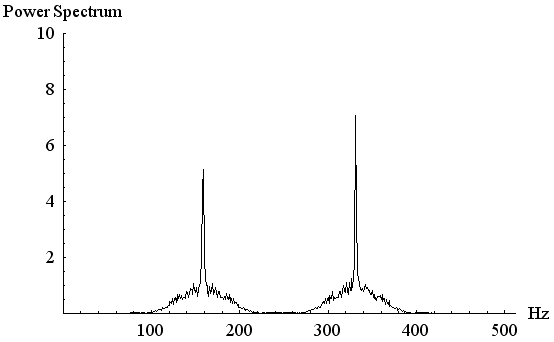
したがって、この変調波の電力スペクトルは、それぞれの発信器の周波数の位置で線スペクトルをもちます。 実際に、VCO方式と発信器切り替え方式について、電力スペクトルをシミュレーションした結果を下に示します。
上がVCO方式、下が発信器切り替え方式の変調波の電力スペクトルです。 VCOでは、両周波数の位置に角のようなスペクトル集中がみられます。 でもこれは線スペクトルではありません。 発信器切り替え方式では、VCOと同程度のゆっくりとした窓で切り出しました。 両周波数の位置に線スペクトルが見られます。 シミュレーション時間が短いので有限の高さで収まっていますが、もっと長くシミュレーションして平均回数を増やせばピークはどんどん高くなってゆきます。 注 : 周波数変調の短所と長所をあげてみます。 |
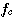 Hz を中心に、送りたい信号
Hz を中心に、送りたい信号
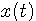 を周波数として表すならば
を周波数として表すならば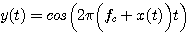
 を
を を取り出せばなんとかなりそうですが、そのカーブを描いてみると下図のようになります。 無限大が出現してダメですね。 それに、受信信号
を取り出せばなんとかなりそうですが、そのカーブを描いてみると下図のようになります。 無限大が出現してダメですね。 それに、受信信号
 の定数倍が不明なので、これは実現不可能です。
の定数倍が不明なので、これは実現不可能です。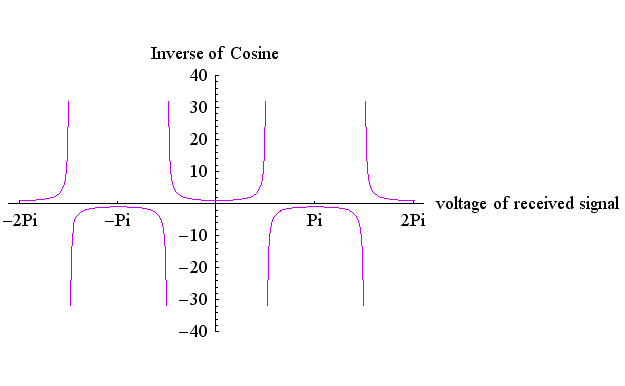
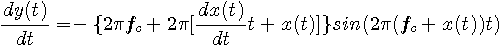
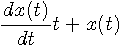

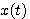 をどうすれば取り出せるでしょうか? 第一項は時間がたてば、どんどん大きくなってしまいそうです。 なんだか、隘路に入ってしまいました。
をどうすれば取り出せるでしょうか? 第一項は時間がたてば、どんどん大きくなってしまいそうです。 なんだか、隘路に入ってしまいました。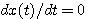 を仮定していたのです。 周波数といえば、延々と一定の振動が続く状況を想像します。 数学的な概念は確かに永遠の単振動を意味しています。
を仮定していたのです。 周波数といえば、延々と一定の振動が続く状況を想像します。 数学的な概念は確かに永遠の単振動を意味しています。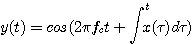
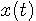 を得ることができます。 ここで、VCOという回路をちゃんと定義しておきましょう。
を得ることができます。 ここで、VCOという回路をちゃんと定義しておきましょう。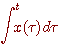 は周波数ではなく「時刻 t での位相」を表しています。
は周波数ではなく「時刻 t での位相」を表しています。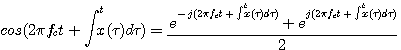
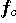 は非常に大きく、
は非常に大きく、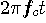 に比べて
に比べて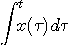 の変化は非常に緩慢です。 したがって、右辺分子の左の項をとってみると、複素平面上に描かれた単位円の上を反時計周りに高速に回転しています。 そして
の変化は非常に緩慢です。 したがって、右辺分子の左の項をとってみると、複素平面上に描かれた単位円の上を反時計周りに高速に回転しています。 そして
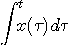 によってちょっとブレーキがかかったり、ちょっと加速されたりしています。 右の項は時計回りの成分です。 二つの項は、かならず複素共役になっているので、反時計回りだけに注目してかまいません。
によってちょっとブレーキがかかったり、ちょっと加速されたりしています。 右の項は時計回りの成分です。 二つの項は、かならず複素共役になっているので、反時計回りだけに注目してかまいません。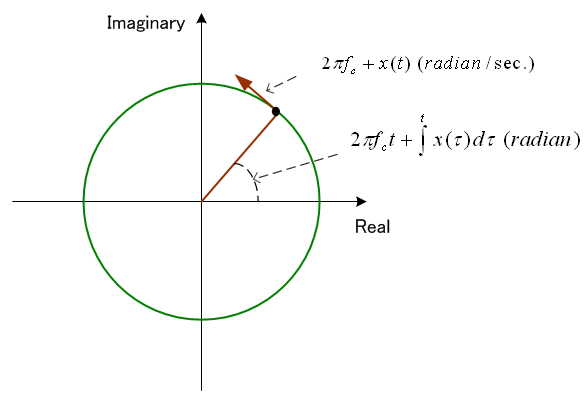
 整流
整流  低域通過炉波
低域通過炉波  DCカット によって、円運動の角速度の変化分
DCカット によって、円運動の角速度の変化分 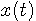 が取り出せることを理解してください。
が取り出せることを理解してください。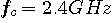 で、
で、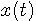 は 1MHz の帯域幅を使っています。 そうすると、いきなり微分した信号の包絡線のDC成分の大きさと、変化分の大きさの比は
2400:1 ということになります。 これでは包絡線の変化分を良い精度で取り出せそうにありません。 そこで、同期検波によって、直接ベースバンドに落とすか、または中間周波数
(IF : Intermediate Frequency) に落としてみます。 前者の場合、
は 1MHz の帯域幅を使っています。 そうすると、いきなり微分した信号の包絡線のDC成分の大きさと、変化分の大きさの比は
2400:1 ということになります。 これでは包絡線の変化分を良い精度で取り出せそうにありません。 そこで、同期検波によって、直接ベースバンドに落とすか、または中間周波数
(IF : Intermediate Frequency) に落としてみます。 前者の場合、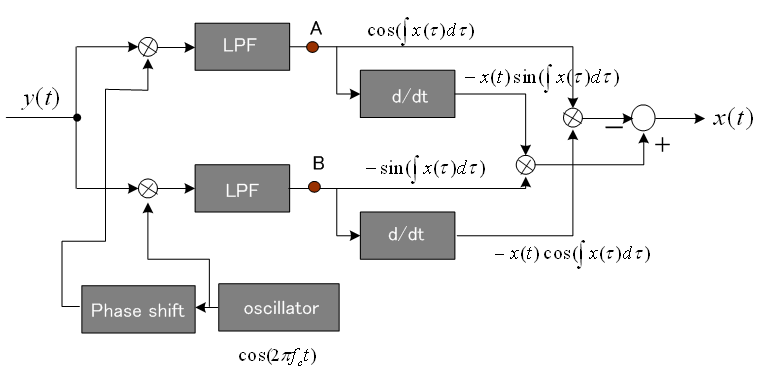
 で回転しています。 右半分のたすきがけ回路では、角速度を取り出しています。 ベースバンド信号の微分操作が入っています。 後者の場合、
で回転しています。 右半分のたすきがけ回路では、角速度を取り出しています。 ベースバンド信号の微分操作が入っています。 後者の場合、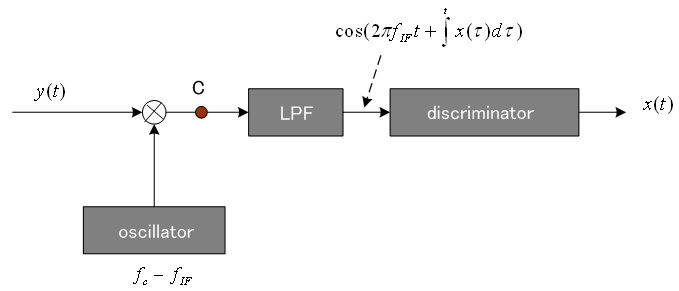
 のフーリェ変換を計算してみると、とりあえず、
のフーリェ変換を計算してみると、とりあえず、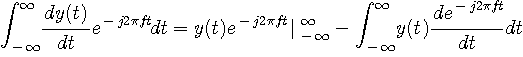
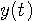 をある時間内でしか存在しないとしておきます。 したがって、右辺第一項をゼロと考えます。 右辺第二項をさらに計算すると、
をある時間内でしか存在しないとしておきます。 したがって、右辺第一項をゼロと考えます。 右辺第二項をさらに計算すると、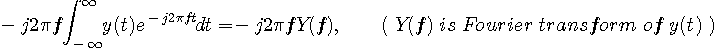
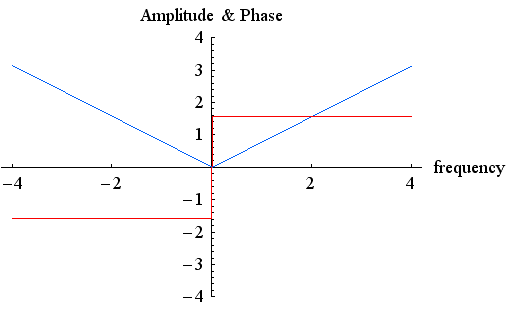
 であることがわかります。 これを振幅と位相で表わすと、
であることがわかります。 これを振幅と位相で表わすと、 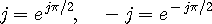 などを用いて、
などを用いて、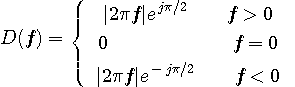
 とすると、差分の周波数特性は、
とすると、差分の周波数特性は、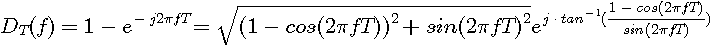
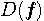 を単純にIF周波数の位置
を単純にIF周波数の位置 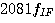 にシフトしても、純粋な微分特性は帯域制限されていないので、
にシフトしても、純粋な微分特性は帯域制限されていないので、