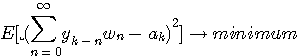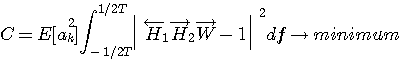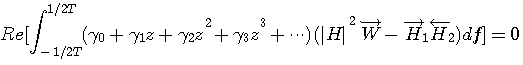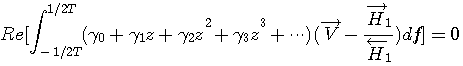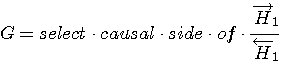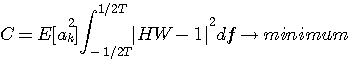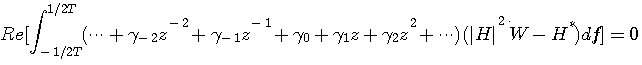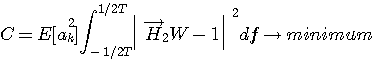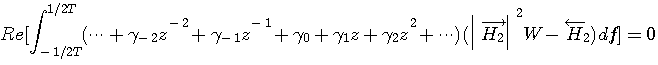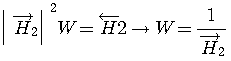|
逆システム Inverse of linear systems |
|
AR(自己回帰)モデルの最適予測は逆システム(等化)になりました。 ARモデルは帰還ループをもっており、予測器は帰還ループをもっていないから、ARモデルが安定ならば、それは最小位相推移です。 予測は本来因果的な操作ですから、信号源モデルが非最小位相推移とすると、ARモデルを前提とする綺麗な議論ができないかもしれません。 少なくとも、”予測=等化”は成立しそうにありません。 では、視点を広げて、等化も含めて、網羅的に検討したらどうなるでしょうか? ここでは、次のようなすべての組み合わせに対して、結果を洗い出してみます。 ただし、簡単のため実信号を前提にします。 複素信号に拡張すると位相の任意性が入るケースがあり、これらの問題はQAMなどの通信処理の場面で多く遭遇します。
非最小位相推移の一般モデルは
さらに、応答の時間シフト補正
とします。 注1: もし、 まず、予測から検討します。 モデルが最小位相推移
の場合は、すでにARモデルで説明したように、因果的最適予測は、
ここで、
評価関数 C
を最小にするには、
に対して、
を満たさなければなりません。 右肩の*は複素共役なので、
となります。 以上から、
ですが、
が成り立っていることから、
が評価関数Cを最小にすることがいえます。 次に、信号源モデルが非最小位相推移
の場合について
です。 ここで、被積分関数については
がいえますから、上とまったく同様に、変分法を用いて、
が得られ、最適予測は次のようになります。
このときのトータルシステムは
となり、非因果的ですが、
なので予測誤差は白色化されます。
次に、等化問題に移ります。 モデルが最小位相推移で等化器が因果的な場合は予測問題と同じです。 モデルが非最小位相推移で等化器が因果的な場合については、以下のようになります。 等化目標は
ですが、これを周波数領域で書くと、次のようです。
今度は、等化器が
任意の摂動に対して上の式が成り立つためには、
の定数項とすべての負ベキがゼロでなければなりません。 正ベキは不定です。 この条件を満たす
として、
となります。 実際には、この連立一次方程式を解けば因果的等化器が得られます。 では、周波数領域で別の表現を導いてみます。 因果的等化器を次のように二つに分解します。
こうすると、
なので、
非因果的等化は、モデルが非最小位相推移の場合は、
から、変分法の結果が
になるので、結局、
となります。 モデルが最小位相推移の場合は、
から、
が解ですが、これは最小位相推移を因果的に等化したときの解と同じです。
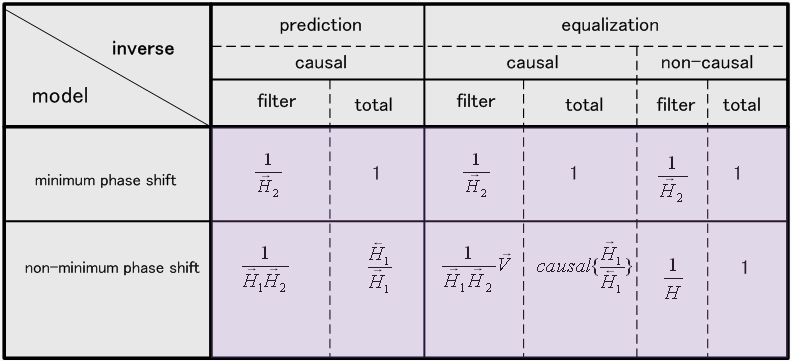
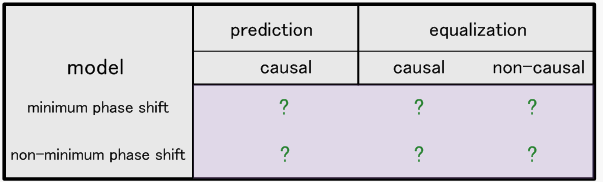
以上を表にまとめると次のようになります。
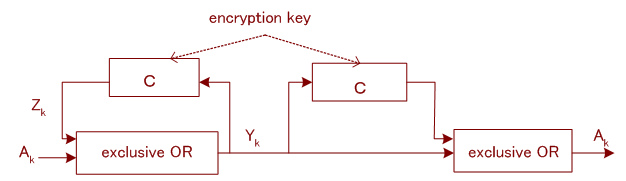
注2: 以上は実数値信号を扱っていましたが、一般にMを法とする(Modulo M の)システムについても、同じような議論が可能。 下図のような因果的なケースが相関符号伝送、 そして、一般化相関符号伝送(THP)で登場します。
特に、2値データを扱うModulo 2 の場合は、暗号システムで応用されており、送信側と受信側の可変回路Cを同じ鍵(たとえば64ビット列)で同一の回路にします。
|
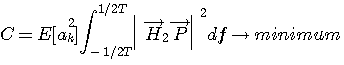
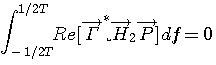
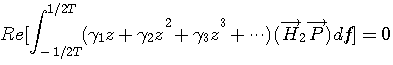
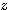 のベキに関して直交関係
のベキに関して直交関係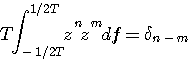
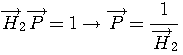
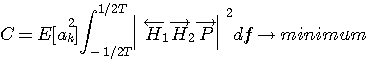
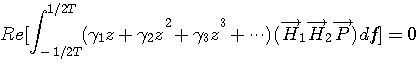
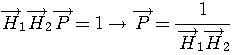
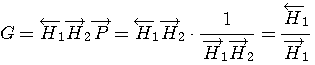
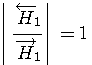
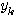 をモデル出力とすると、
をモデル出力とすると、