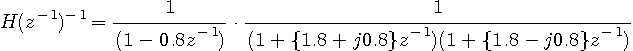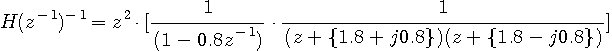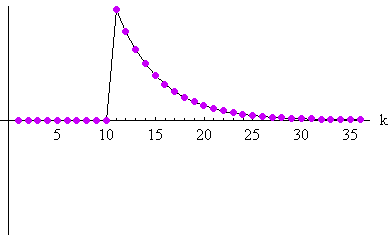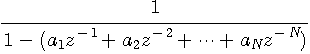次の因果的なＦＩＲディジタルフィルターの逆フィルターを求めたいとします。

単純に の逆数をとると、

ですが、右辺の左の分数は安定、右の分数は不安定になって（発散して）しまいます。　この場合、 の逆フィルターは因果的な範囲で存在しないことがわかります。　一方、 の振幅スペクトルは下図のようになっています。

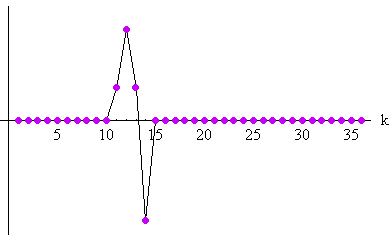
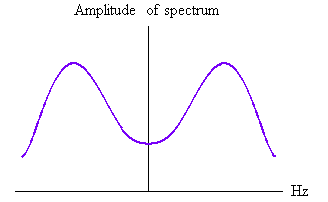
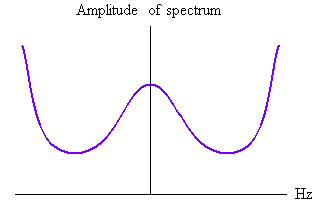
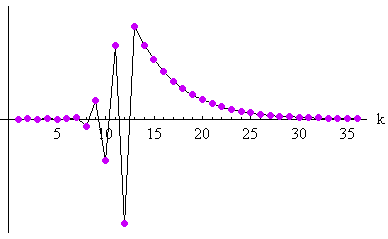
このスペクトルはゼロをもたないので、逆数は下図のように有限の範囲で求まります。

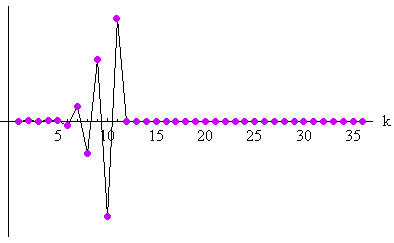
したがって、 の周波数特性を求めて（ を代入して）、これをフーリエ逆変換すれば、下図のように有限な大きさの応答が得られます。　この応答は一体なにを意味するかを考えてみます。

の右の分数の分子と分母に を掛け、次のように変形します。

[  ] 内の左の分数はそのままですが、右の分数の分母は の２次多項式になっています。　そして、この分数は のベキ級数に展開できます。　すなわち、反因果的（anti-causal) に安定といえます。　下図は右と左の分数のベキ展開（応答）を表しています。　ともに、横軸の k=11 のところが [  ] 内の時間の原点です。　

時間原点を k=11 に固定して、二つの応答のコンボリューションをとり、それを２時刻だけ右にシフトすると（ を掛けることは、応答を２時刻早めることに相当する）、ちょうど の応答に一致します。　すなわち、この応答を、 k=13 の時刻を時間原点として、そのまわりで因果的安定な逆と反因果的安定な逆に展開できたことになります。

 このような操作は多項式の因数分解によって決まりますが、
因数分解は一意ですから、時間原点も一意に決まります。

もし、最初に与えられた因果的フィルター（一般に、多項式の分数でもかまいません）、

の逆数がそのまま安定であるとき（因果的逆をもつとき）、そのフィルターを最小位相推移と呼んでいます。　一般には、上の例題のように因果的安定な逆をもたないので、遅延を許して（位相推移をして）両側安定の形を求めなければなりません。

ＡＲモデル、

は因果的です。　この逆は、最適予測システム（因果的）

でした。　したがって、ＡＲモデル自身が安定ならば、それはいつも最小位相推移です。