|
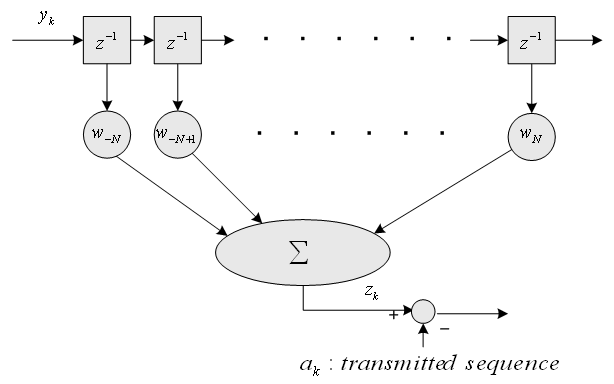
下はシンボルレート等化の構造です。
確率的勾配法等化アルゴリズムの収束速度は、受信信号の自己相関行列
 の固有値のバラツキに強く依存しました。 もし の固有値のバラツキに強く依存しました。 もし  が予め分かっており、それが正則(逆行列が存在する)としたら、確率的勾配法を次のようにすれば収束が速くなるはずです。 ここで、 が予め分かっており、それが正則(逆行列が存在する)としたら、確率的勾配法を次のようにすれば収束が速くなるはずです。 ここで、 は時刻 k でシフトレジスターの上にある受信信号ベクトル、 は時刻 k でシフトレジスターの上にある受信信号ベクトル、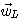 はアルゴリズム実行回数 L でのタップ重みベクトルを表しています。 はアルゴリズム実行回数 L でのタップ重みベクトルを表しています。
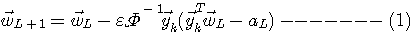
実際、両辺の期待値をとると、
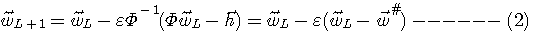
となって、タップ重みベクトル  の期待値 の期待値 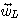 の各要素が同じスピードで最適解 の各要素が同じスピードで最適解 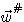 に収束することがいえ、修正係数を大きく選ぶことができます。 しかし、現実には相関行列を予め知ることができないので、アルゴリズムの進展に沿って、相関行列の逆行列も漸化式で更新して に収束することがいえ、修正係数を大きく選ぶことができます。 しかし、現実には相関行列を予め知ることができないので、アルゴリズムの進展に沿って、相関行列の逆行列も漸化式で更新して
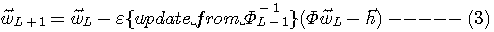
のようなことができれば、収束を速めることができそうです。 時刻 k=1から始まり、 k=L になったときの、自乗誤差の総和
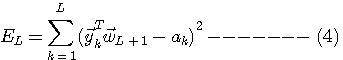
を最小にするタップ重みベクトル 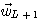 は は
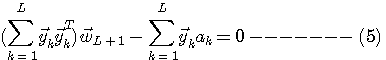
の解です。 これを改めて、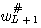 で表します。 同様に、1時刻前の k=L-1 での解 で表します。 同様に、1時刻前の k=L-1 での解 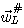 は次式を満たします。 は次式を満たします。
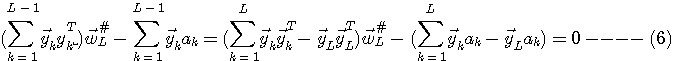
この式を、見やすくするために、
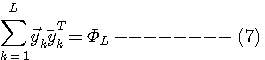
とおいて、式(4)と式(5)から次のように書きます。
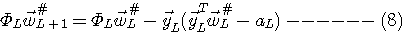
この式は、L=1,2,3,・・・における最小自乗誤差の解を具体的に与える漸化式を意味しています。 言い換えれば、この式で更新された
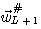 は時刻 L までの自乗誤差を正確に最小にしています。 漸化式(8)を実行したいのですが、相関行列 は時刻 L までの自乗誤差を正確に最小にしています。 漸化式(8)を実行したいのですが、相関行列
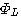 の逆行列が必要になってきます。 それならば、式(7)によって得られる の逆行列が必要になってきます。 それならば、式(7)によって得られる 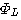 の逆行列を式(8)に左から掛けて、 の逆行列を式(8)に左から掛けて、
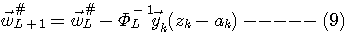
を実行すれば、式(3)の意味をもつ高速収束アルゴリズムが得られるのですが、そうすると逆行列の計算を毎回実行しなければなりません。 この計算量はベクトルの次数
(2N+1) の3乗に比例し、現実的ではありません。 実際、ロールオフ率の小さいパルスを用いた電話回線用アナログモデムやADSLやCATVなどの有線通信では、40〜60に達します。 そこで、逆行列
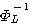 を漸化式で次々と更新することが鍵になりますが、それは下の逆行列の補助定理
(Matrix Inversion Lemma ) によって、 を漸化式で次々と更新することが鍵になりますが、それは下の逆行列の補助定理
(Matrix Inversion Lemma ) によって、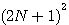 に比例する計算量で実現できます。 に比例する計算量で実現できます。
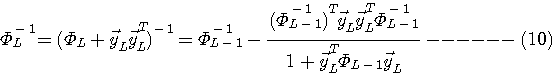
この右辺を計算すればいいわけですが、これを式(9)に代入したときのベクトル、
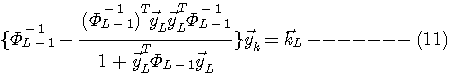
を効率よく算出する手順として以下を得ます。 ここで、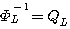 とおき、次の媒介ベクトルと変数を導入しています。 とおき、次の媒介ベクトルと変数を導入しています。
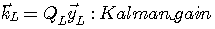
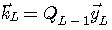
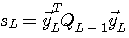
この手順によって陰に決まっていく自己相関行列を 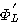 とします。 これは正確に とします。 これは正確に 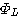 ではなく、以下のように決まります。 ではなく、以下のように決まります。
アルゴリズムの初期段階では、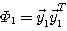 は ランク=1 の行列なので、本来、この逆行列は存在しません。 さらに、逆行列は は ランク=1 の行列なので、本来、この逆行列は存在しません。 さらに、逆行列は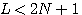 までは存在しないのですが、行列 までは存在しないのですが、行列 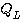 は上から分かるように、 は上から分かるように、
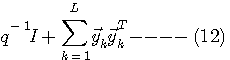
の逆行列を陰に求めています。 したがって、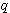 の大きさが の大きさが 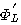 と と 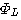 の近似の度合いを決めており、 の近似の度合いを決めており、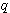 が大きいほど良い近似を与えます。 が大きいほど良い近似を与えます。
このアルゴリズムの収束の様子は、 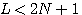 までは収束せず、 までは収束せず、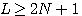 になって自己相関行列 になって自己相関行列 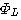 がフルランク(正則)になったとたんに急激に収束します。 その後の微細な収束は、 がフルランク(正則)になったとたんに急激に収束します。 その後の微細な収束は、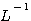 に比例する速度になります。 に比例する速度になります。
以下に、簡単な例でシミュレーションしてみます。 チャンネル歪を
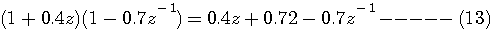
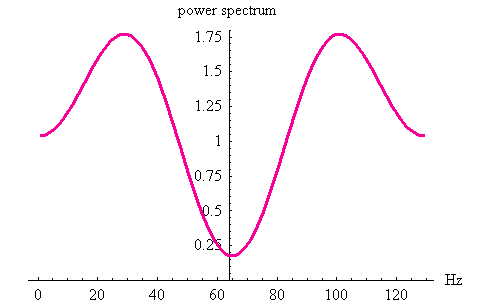
としてみます。 この周波数特性の自乗(送信信号をランダムとしたときの受信信号の電力スペクトル)は下図のようであり、受信信号の自己相関行列の固有値は、このサンプル値に近いので、かなりバラつくことが予想されます。
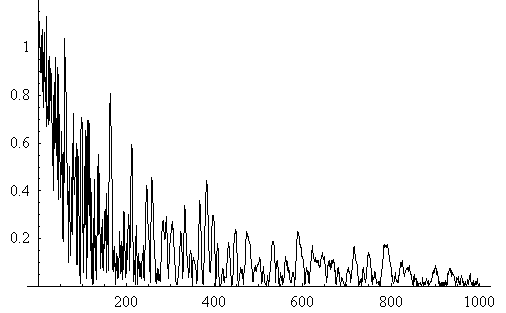
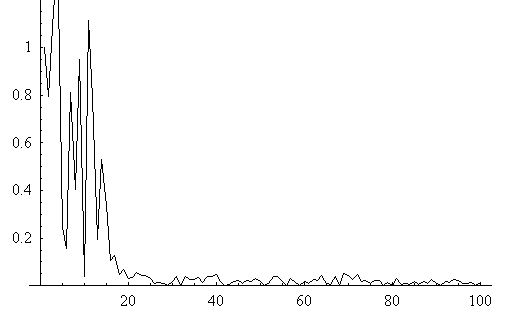
15タップでシミュレーションしたときの等化誤差 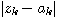 を下にプロットします。 初期値は を下にプロットします。 初期値は 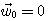 です。 上の図が通常の確率的勾配法、下が高速収束 ( です。 上の図が通常の確率的勾配法、下が高速収束 ( 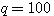 ) を示しています。 横軸は修正回数であり、その長さが、上の1000に対して、下は100であることに注意してください。 ) を示しています。 横軸は修正回数であり、その長さが、上の1000に対して、下は100であることに注意してください。
注1: この高速収束法は
Godard D "Channel Equalization Using a Kalman Filter for Fast Data Transmission"
IBM J., Res. and Dev., Vol.18, pp267-273, May, 1974
によるものですが、Kalman filter (Rudolph
E.Kalman)
の応用になっています。 つまり、上の手順は、受信ベクトル  を観測フィルタと見做し、これが時々刻々変化する状況でチャネル応答(ここでは時間不変とした)を推定するカルマンフィルターと見做すことができます。 を観測フィルタと見做し、これが時々刻々変化する状況でチャネル応答(ここでは時間不変とした)を推定するカルマンフィルターと見做すことができます。
|



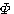 が予め分かっており、それが正則(逆行列が存在する)としたら、確率的勾配法を次のようにすれば収束が速くなるはずです。 ここで、
が予め分かっており、それが正則(逆行列が存在する)としたら、確率的勾配法を次のようにすれば収束が速くなるはずです。 ここで、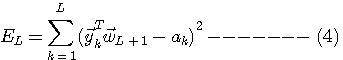
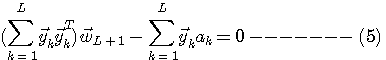
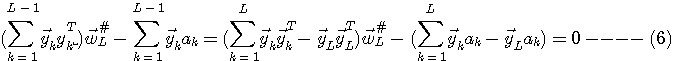
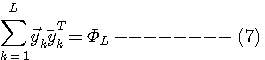
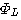 の逆行列を式(8)に左から掛けて、
の逆行列を式(8)に左から掛けて、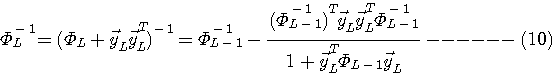
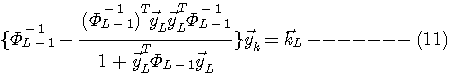



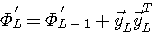
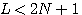 までは存在しないのですが、行列
までは存在しないのですが、行列 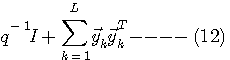
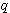 の大きさが
の大きさが 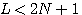 までは収束せず、
までは収束せず、
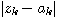 を下にプロットします。 初期値は
を下にプロットします。 初期値は 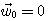 です。 上の図が通常の確率的勾配法、下が高速収束 (
です。 上の図が通常の確率的勾配法、下が高速収束 ( 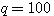 ) を示しています。 横軸は修正回数であり、その長さが、上の1000に対して、下は100であることに注意してください。
) を示しています。 横軸は修正回数であり、その長さが、上の1000に対して、下は100であることに注意してください。

 を観測フィルタと見做し、これが時々刻々変化する状況でチャネル応答(ここでは時間不変とした)を推定するカルマンフィルターと見做すことができます。
を観測フィルタと見做し、これが時々刻々変化する状況でチャネル応答(ここでは時間不変とした)を推定するカルマンフィルターと見做すことができます。