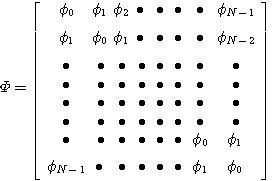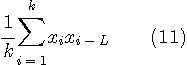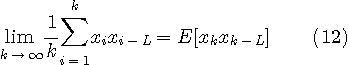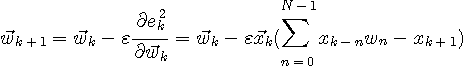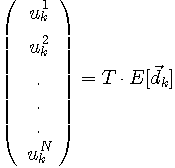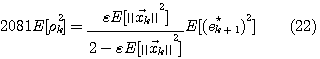|
適応線形予測 Adaptive linear prediction |
|
一般に、「予測」と言えば、台風の進路予測やマクロ経済のＧＤＰ予測など、非常に複雑なシステムを思い出します。仮に、線形近似が成り立つならば、変数は各種指標を要素とするベクトルであり、予測したいパラメータは行列の系列になります。多次元の難しさは、多くの場合において指標の間に相関関係があることであり、この相関関係を断つような独立成分分析が必要になります。ここでは、最もシンプルな単一指標（一次元）について、しかも、定常な外乱を前提とした予測問題の基本を解説します。 線形予測は、もし対象が全時間帯に渡って確率的定常ならば、後述するように、予測器の重み係数がYule-Walkerの方程式の解に収束することが最適です。しかし、工学的応用では、「全時間帯で定常」という前提は現実的ではありません。実用的には、有限の時間帯において定常性が許容できるとして、予測誤差の時系列が小さくなるような適応的アルゴリズムを採用することになります。 そこで、 定常な確率的モデルから出力される信号を、一定時間毎に計測した系列を
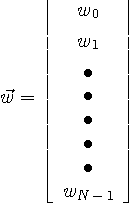
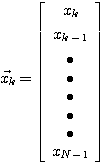
で表します。 現在までの時系列を用いて、次の時刻のデータを予測したい。 この予測値を一次結合、
で計算します。
で表します。適応線形予測の計算は、新しい計測値を得るたびに、自乗誤差
線形予測システムのブロック図
まず、このような重み係数の最適解を求めます。自己相関を次のように期待値で表します（適応アルゴリズムの文脈からすれば、後述のように時間平均で表すべきです）。
そして、予測誤差の自乗平均
を最小にする重み係数を求めてみます。 重み係数を連続的に変えれば、評価関数Ｃも連続的に変わることは明らかです。 次に、Ｃが重み係数に関して下に凸であることを確認します。下に凸であることは、任意の２点のＣの値を結ぶ内挿点が、２点の内挿点のＣの値よりも大きいことを意味します。
ここでは、重み係数を要素とするベクトルを扱いますから、凸性はベクトル空間で確認しなければなりません。 まず、Ｃを見やすい形にします。
ここで、
行列 定理 定理 評価関数
とし、
式（７）の不等号は、 定理 から得られます。 したがって、
すなわち、
を解いて、最適重み係数を一意的に得ることができます。 この連立方程式を Yule-Walker の方程式と呼んでいます。 さて、この解を実際に求める問題に移ります。 いままでは、 すべての起こりうる時系列を念頭において、 という操作を前提にしてきましたが、これはとても抽象的な概念です。 実際には、二度と時間を遡って別の時系列を繰り返してくれませんから、こんなことは不可能です。 我々が入手できるのはたった一つのサンプルです。 そこで、自己相関を時間平均
で置き換えるしかありません。 もし、時系列の長さが十分に長ければ、概ね、
が成り立つことを拠り所にすることになります。 この拠り所をエルゴード性と言っています。 したがって、十分多くのデータを溜め込んで、その相関の時間平均をとって、オフライン的に Yule-Walker の方程式を解けば最適な重み係数を得ることができます。 これも一つの具体的方法ですが、ここでは、データを受ける度に、重み係数を少しずつ修正する適応アルゴリズムを考えてみます。 とりあえず、次のように予測誤差の瞬時値をちょっとだけ小さくするように重みを修正してみましょう。
この修正をどんどん続けるとどうなるかを考えます。 Yule-Walker
の方程式を満たす理想解を
まず、
のようになり（ I は単位行列）、相関行列のすべての固有値が正であることから、 定理
が得られます。 この式から、固有値が小さいほど、それに対応するスカラー式の収束が遅くなることが分かります。 したがって、固有値のバラツキが大きい信号の式（１３）による適応予測は大変難しいことが予想されます。 収束後においては、 以下、収束後の予測誤差を計算しておきます。 この誤差は、理想解に固定した状態での予測誤差と上記の徘徊によるゆらぎの成分の和になるはずです。 式（14）の両辺のノルムを計算してみます。
ここで、
式（１９）の最後の｛ ｝は、収束後の徘徊成分が理想解での予測誤差と相関をもたないことからゼロになり、結局、次が得られます。
さらに、収束後では、
なので、
結局、アルゴリズムの揺らぎを含めた予測誤差は
となります。 なお、時間域での収束の直感的解釈については、確率的勾配法を参照してください。 注１： ここまでは、Ｎ が十分大きいとしてきました。 実際には Ｎ は不明ですが、予測誤差と信号との間に相関が認められない範囲で、 Ｎ を小さくすることができます。 統計学では、Ｎの決定にＡＩＣ(Akaike Information Criteria)を用いることが多いですが、実時間処理を強いられる通信の信号処理では適用が難しいかもしれません。 線形予測は重要な概念と関連しており、要約すると以下のようです。 以下、適応予測の収束の様子をシミュレーションで確認します。
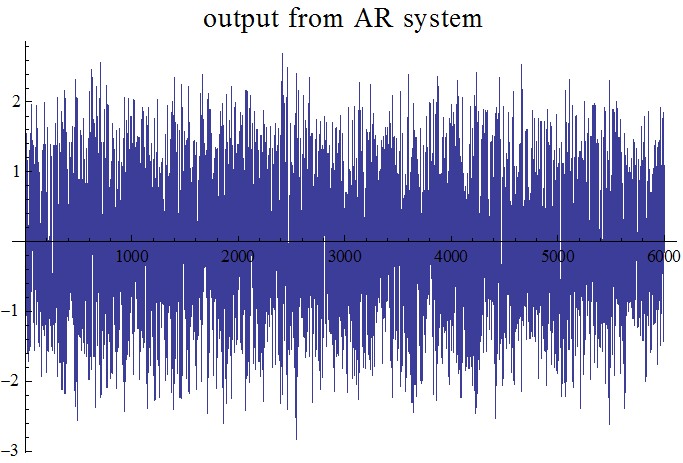
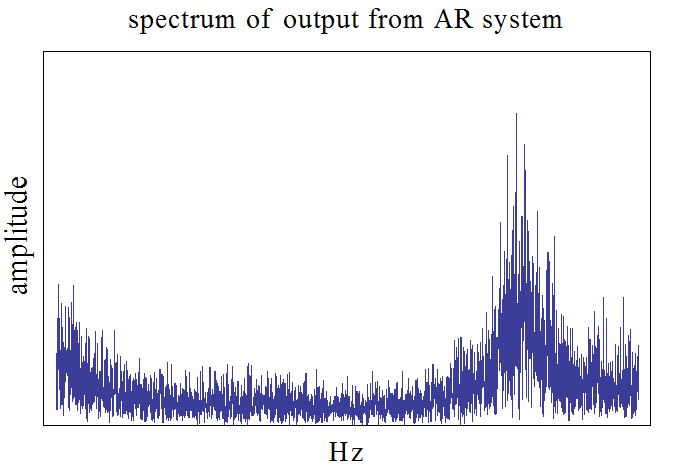
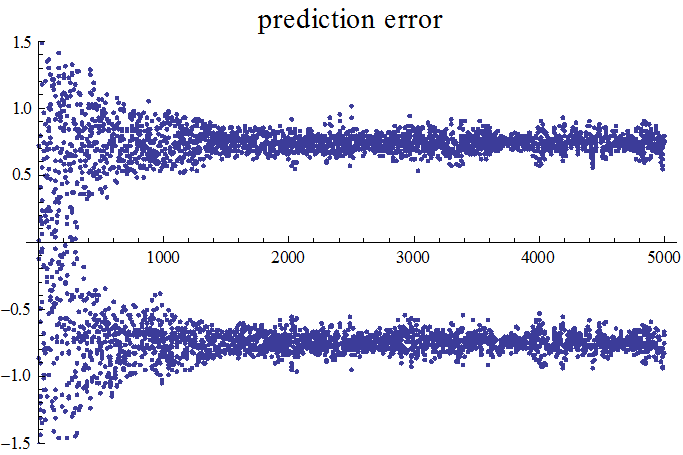
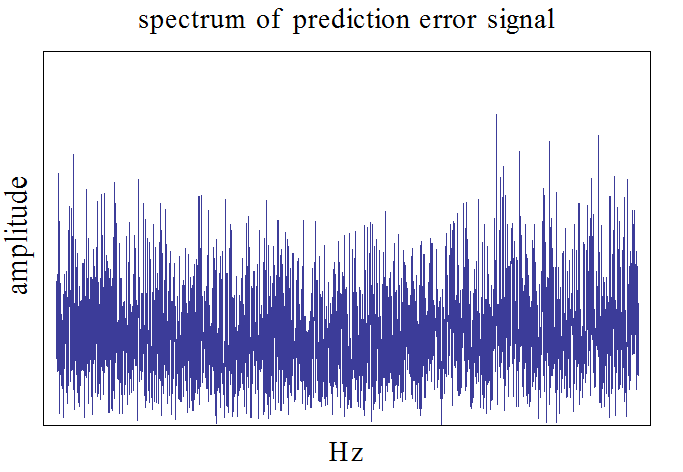
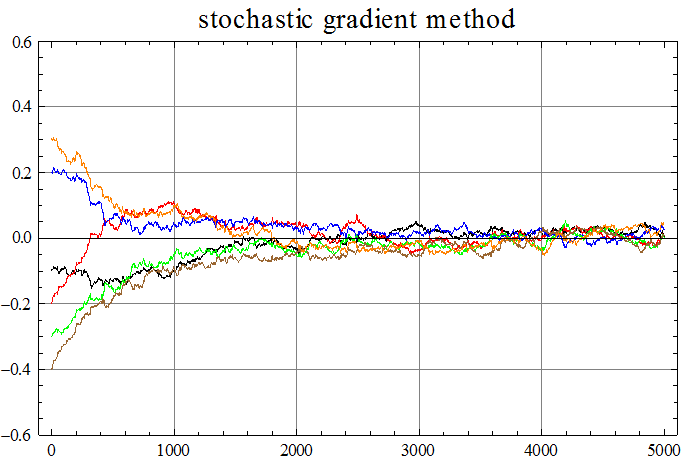
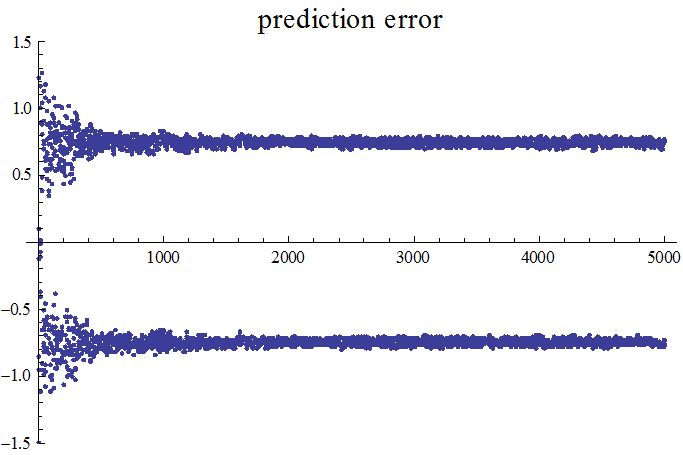
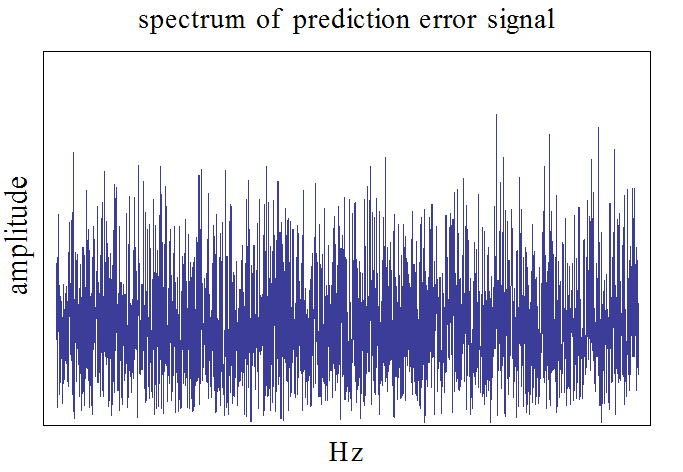
この信号に対して、６個の重み係数による適応線形予測を実行します。下の３つの図は、確率的勾配法によるシミュレーション結果です。修正係数は、収束後の誤差と収束時間がベストになるように調節しました。図は上から次のようです。予測誤差系列、予測誤差系列のスペクトル（平坦になっています）、予測器の重み係数とＡＲシステムの重み係数の差（全部で６つ、６色で描いています）。
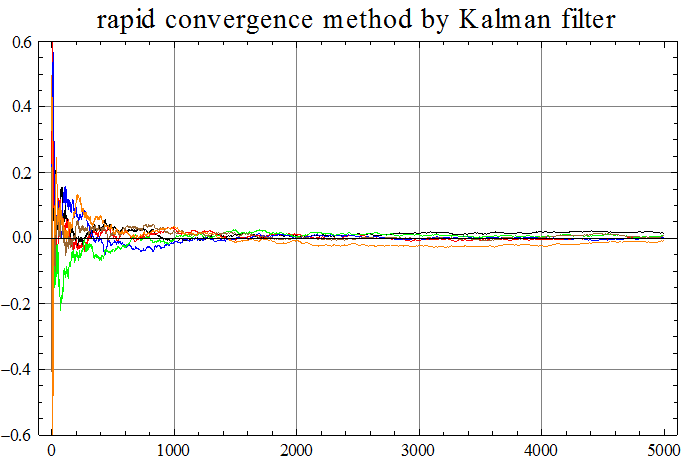
ＡＲシステムの出力スペクトルに急峻な山があるので、自己相関行列の固有値のバラツキが大きくなり、確率的勾配法の収束速度は非常に遅くなります。これを解決するためには高速収束アルゴリズムが有効であり、次のような結果になります。
|
は次の時刻の予測を表しています。 その予測誤差を
が小さくなるように、重み係数 (
) を修正することです。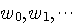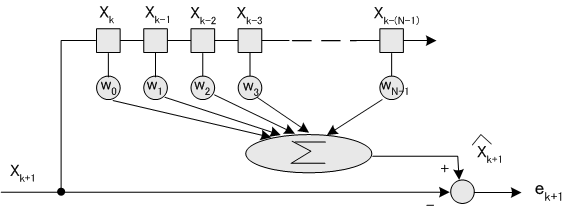
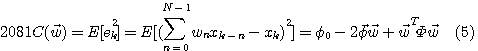
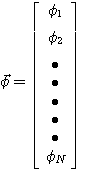であり、肩付きの Ｔ は転置を示します。 ベクトルと行列は下のようです。
, 
は自己相関行列と呼ばれており、
の凸性は次のように確認できます。 途中の計算は省きますが、
と 
を任意として、凸性の確認が以下のように得られます。
はすり鉢状の曲面をしており、その極小は一ヶ所であり、そこではどの方向の勾配もゼロであることが言えました。 以上から、連立方程式
で表し、この解と 
の差 
を用いて上のアルゴリズムを書き換えると次のようになります。
は重み係数が理想解に固定された状態での予測誤差を意味します。 予測誤差と過去のデータの相関は、Yule-Walker
の方程式そのものですからゼロベクトルになります。 
の期待値の変化をみるために、式（１４）の両辺の期待値をとって、式（１５）を代入すると、
を式（１４）が発散しないように小さく選んで、
をゼロベクトルに収束させることができます。 収束の様子をみるために、式（１６）を次のようにスカラー方程式に分解します。 そのために、次の定理を用います。
は、適当な正規直交行列 
によって次のように直交化できる。
は固有値 
を対角項とする対角行列。
は対称行列なので、上の定理を式（１６）に適用することができ、スカラー式への分解
は完全にゼロになるわけではなく、ゼロベクトルの周りをフラフラと徘徊し、その範囲や速度は係数
の大きさによって決まります。 この徘徊は、式（１５）からベクトル 
に無相関でなければなりません。 もし、相関が残っていれば、まだ完全に予測誤差を最小化していないことになります。
は徘徊による揺らぎ成分であり、これを 
とおいて、上式の期待値をとります。 ただし、
はレジスタに記憶されているデータの自乗和（大きな正数）であり、これを定数とみなします。
