

|
通信路の符号化 Channel coding |
|
シャノン (Shannon )の通信路符号化定理はディジタル通信の基礎であり、すべての人がこの恩恵にあずかっているといっても過言ではありません。 ただ、この定理をシャノンの論文にしたがって一般的に証明すると、話が抽象的になってしまいます。 そのため、シンボルが2値(1と0)の伝送を例にとって、直感的な具体例で話を進めてみます。 通信路の符号化は、簡単にいえば次のような内容です。 通信路符号化定理 通信路容量(単位はビット/シンボル)よりも A Mathematical Theory of Communication 1948 この定理でいう「通信路容量」とは、平たくいえば、チャンネルが発揮できる最大の通信能力を指します。 チャンネルは、ある種の送信信号を通しやすいとか、ある種の送信信号を通しにくいといった性質をもちますが、もっとも通しやすい信号を送っている状態でのチャンネルの情報通信能力を意味します(雑音が白色ガウスのときの通信路容量、更に、雑音が有色ガウスのときの注水定理を参照)。 *誤り率を無限に小さくする 11111 のように5回続けて1を送るとしましょう。 そして、これを受けた受信者は多数決で判定すると考えます。 もし、0が3個または4個または5個ならば、0に誤判定されてしまいます。 この誤り率は となります。 ここで で計算されます。 したがって、反復数 n を増やせば、下図のように誤り率を無限に小さくできます。 縦軸は誤り率の常用対数です。
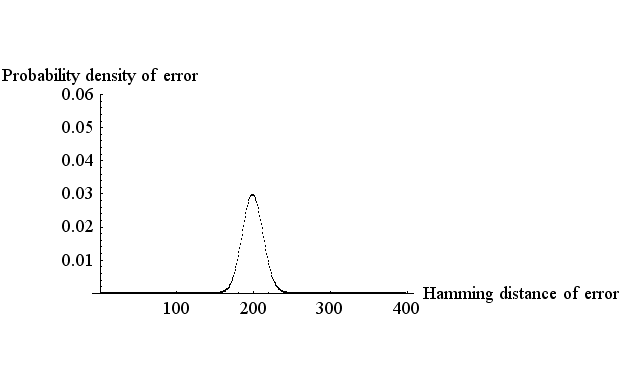
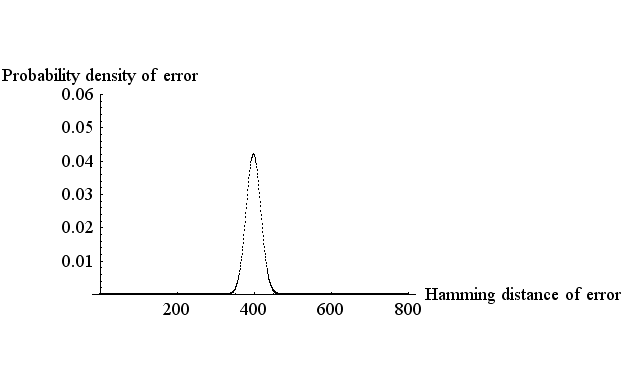
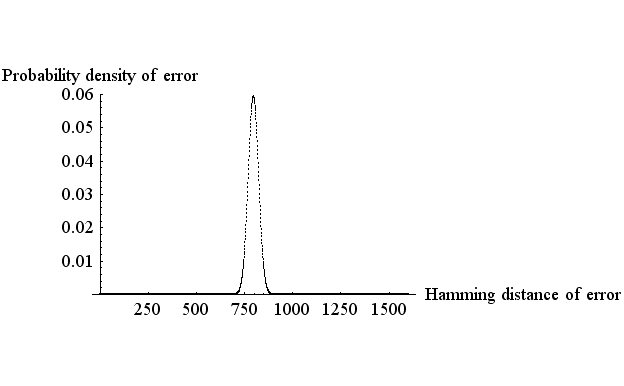
しかし、この方法で誤り率をゼロにしようとすると、通信速度を無限に小さくしなければなりません。 これに対して、シャノンは 誤り率を無限に小さくするには、 ということを主張しました。 以下にその理由を説明します。 注1:シャノン理論は定常ガウス雑音(雑音発生の確率的メカニズムは時間的に不変)を前提にしています。雑音が周期定常( cyclostationary )のときは、繰り返し伝送方式とシャノン方式の優劣は逆転することがあります。ロバスト伝送を参照してください。 まず、ハミング距離を定義します。 下の二つのフレームをみてください。 A: 000111010100111010 B: 010111000100110010 フレームA を送って、フレームB を受けたと考えてください。 赤色で示した3個所でシンボルが誤っています。 このとき、フレーム A とフレーム B のハミング距離は3 であるといいます。 では、フレーム長をだんだん大きくしながら、ハミング距離の誤り率がどのように分布するかを調べてみましょう。 一つのシンボルを送信したときの誤り率を 0.1 とします。 このとき、フレームを長くすると、 下図は、誤りのハミング距離の確率密度を示しています。 上からフレーム長が 2000, 4000, 8000 の場合を示しています。 横軸の目盛りが縮尺されていることに注意してください。
この縮尺でみると、フレーム長が長くなるにしたがって、確率密度が 0.1×フレーム長
のところにどんどん集中して行くことがわかります。 言い換えると、フレーム長 誤りのハミング距離の密度 > を考えてみると、
*送信フレームの個数
この想定が正しければ、速度を一定比率落とすだけで、誤りのない通信ができます。 その代わり、フレームを全部受信しないと送信信号を判定できないので、無限に長いフレームは理論としての概念です。この辺のことは、現実から離れて考えてください。
さて、まだ大きな疑問が残っています。 その疑問は次のようです。 上で選択された送信フレームの個数(これを
M とする)は すなわち、限定されたM個のフレームを用いて、
の速度で情報を送ることができますが、もしMがフレームを長くしてもあまり大きくならないようなら、反復送信と大差ないということになります。 上の疑問は、フレーム長をどんなに長くしても、 が一定値以下にならないという答えを期待しています。 実は、このことを2値伝送以外の一般的なケースで証明するのは大変抽象的でやっかいなので、できるだけ直感的な解釈を試みましょう。 まず、Mの大きさに見当をつけましょう。 可能なフレームの個数は全部で したがって、この 上式右辺に注目し、これを具体的に計算してみます。 下図は、フレーム長
上図の連続的なオレンジ色のカーブが通信路容量であることが通信路符号化定理のポイントですが、オレンジ色の限界を上回る速度ではどんなにフレームを長くしても誤り訂正の見逃しは小さくなるが急速にゼロに収束できません。逆に、この限界以下の速度での安全運転では、フレーム長をそこそこ長くすれば、誤り訂正の見逃し率を急速にゼロにできることを暗示しています。実用的な設計では、この限界以下の速度で、フレーム長のトレードオフを設計することになります。 以下、誤り率が小さい範囲での補足的な検討です。 誤り訂正の対象となるチャンネルのシンボル誤り率を
0.01 ぐらいとすると、この周辺では(上図の左端では) この図の縦軸をフレーム長 を描くと下図のようになります。 上の直線が
2本の線は
として一体どうなるのか、ちゃんと確認しておく必要があります。 ちょっと退屈かもしれませんが、しばらくは近似論を追跡しましょう。 まず、 さらに、分母にスターリングの公式を用いると、 となります。 半径 ですが、 のような不等式を満たします。 ここで各辺の対数をとります。 右辺の対数は ですが、 となります。 2値無記憶情報源のエントロピーを測る関数 は、 ですが、これを上に代入して、 が導かれました。 この近似を用いて、送信可能な最大情報量が によって与えられることがいえました。 また、 なので、 がいえます。 以上では、もっぱら半径 セルの数は実際に設計できるフレーム符号の個数の上限を与えていますが、
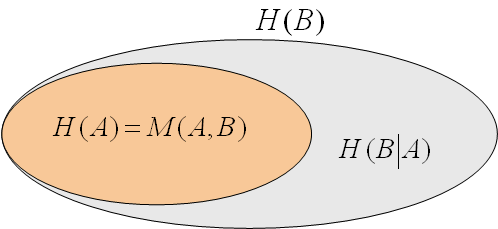
*通信路容量との関係 では、通信路符号化定理にいう通信路容量との関係はどうなっているでしょうか? これについては 相互情報量 をもう一度復習する必要があります。
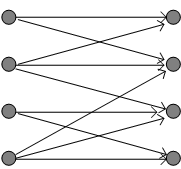
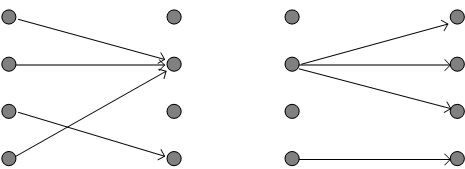
このようなグラフの中で、次の二つは大変特徴的です。 枝のないところは確率がゼロです。 左のグラフは、送信シンボルのグループが同一のシンボルに判定され、それらのグループは互いに交わっていません。 逆に、右のグラフは、送信シンボルが誤る先のグループが互いに交わっていません。 まず、左の場合について
ここで、4つの対数関数の変数はすべて1 なので、 が言えます。 したがって、 が結論できます。 次に、右のグラフの場合では、誤らないにしろ、誤るにしろ、判定結果はいつも唯一の送信シンボルを確率 1 で指しています。 このことは、すべての事後確率が 1 であることを意味していますから、 すなわち、 が結論されます。 この結果をそのまま翻訳すれば、”チャンネルの相互情報量が送信信号の平均情報量に等しい”
ですが、分かりやすくいえば、”チャンネルは送信情報を損失無く伝送している”
といえます。 となっていることがいえました。 このとき、通信路容量(送信情報源をいろいろ選んで、相互情報量を最大化した状態)は、 となります。 すなわち、誤りのない状態では、情報源の最大エントロピーがそのまま通信路容量になります。 さらに、いままで仮定してきた対称チャンネルの場合は、相互情報量でみたように、 のようにチャンネルの誤り確率 十分長い長さ
注2: 上の通信路容量は2値符号の誤りモデルから引き出されたものである。 広く用いられる通信路容量として、アナログ値伝送と加法的ガウス雑音を仮定して求めた通信路容量
がある。 この公式がディジタル通信にどの程度あてはまるか確認する必要がある。 実際の多値ディジタル通信の場合、2値ビット列の平均ビット誤り率
|
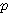 とします。 誤り率を改善する方法として、まず思いつくことはシンボルを反復して送ることです。 たとえば、
とします。 誤り率を改善する方法として、まず思いつくことはシンボルを反復して送ることです。 たとえば、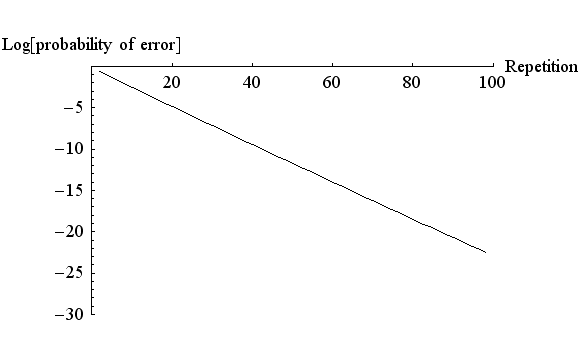
 をどんどん長くすると、誤りのハミング距離の密度が
をどんどん長くすると、誤りのハミング距離の密度が 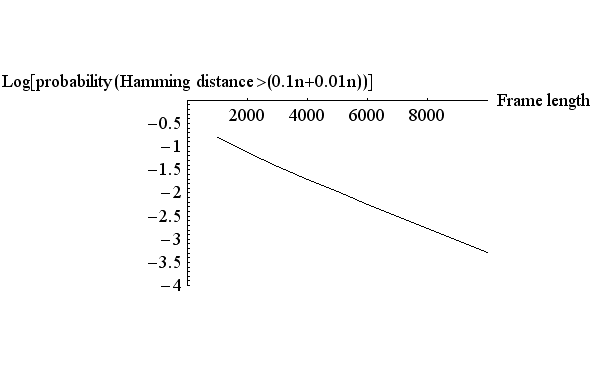
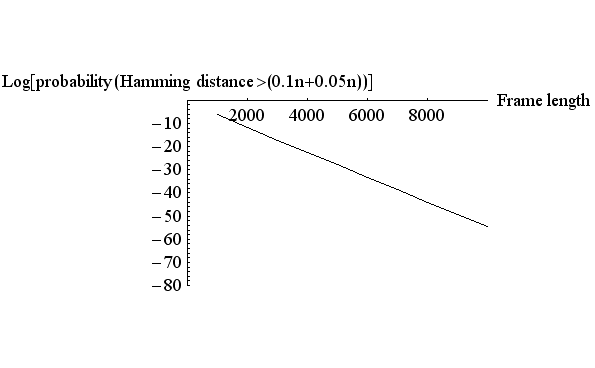
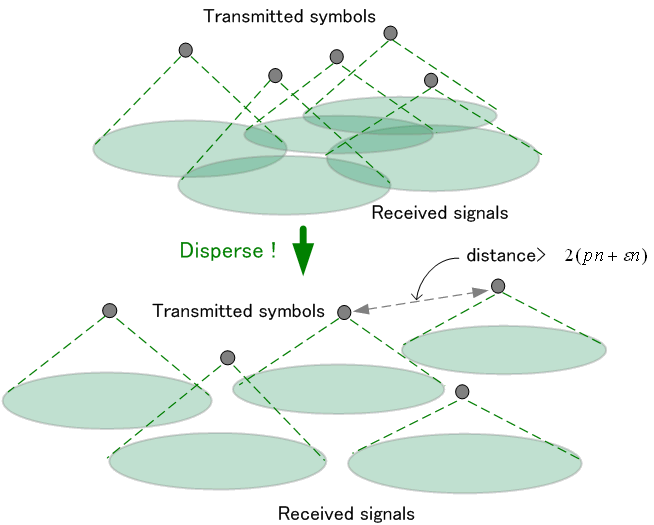
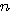 が32ビット、64ビット、128ビット、256ビットの場合について、ハミング距離が互いに
が32ビット、64ビット、128ビット、256ビットの場合について、ハミング距離が互いに
 で割った値を表しています。 この意味は、誤りを訂正するために情報伝送速度を落とさなければならないレートです。 横軸は誤り率
で割った値を表しています。 この意味は、誤りを訂正するために情報伝送速度を落とさなければならないレートです。 横軸は誤り率  を十分に大きくしたときの極限を表しています。オレンジ以外の階段状のカーブでは、誤り訂正の見逃し率は小さいが、完全にゼロではありません。
を十分に大きくしたときの極限を表しています。オレンジ以外の階段状のカーブでは、誤り訂正の見逃し率は小さいが、完全にゼロではありません。
 で割って規格化し、二つのカーブ
で割って規格化し、二つのカーブ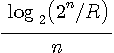
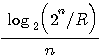 です。
です。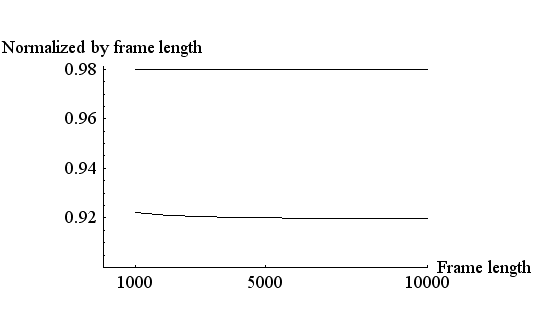
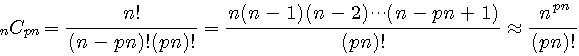
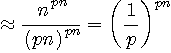
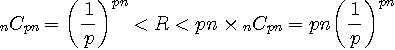
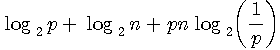
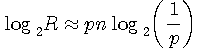
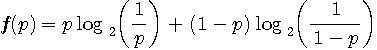
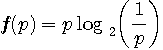
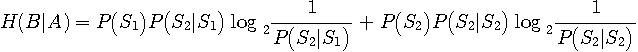
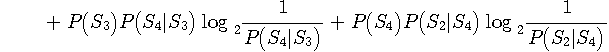
 の2値シンボルからなるフレームを用いて通信したい。
の2値シンボルからなるフレームを用いて通信したい。 ビットの情報を運ぶことができる。
ビットの情報を運ぶことができる。