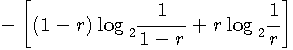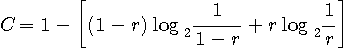|
通信路容量 Channel capacity |
|
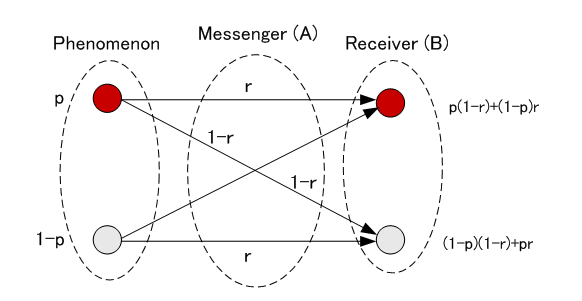
相互情報量は送信信号の情報が受信信号にどれだけ含まれるかを測る尺度でした。 送信者をA で表し、受信者をB で表すと、相互情報量は
で与えられます。 送信者もチャンネルも無記憶とすると、相互情報量は送信シンボルの確率分布とシンボル誤り率が与えられれば計算できます。 シンボルの誤り率はチャンネルの特性であり、送信シンボルの確率分布は送信情報源の特性です。 したがって、送信シンボルの確率分布
を通信路容量（Channel Capacity）と呼んでいます。 Shannon "A Mathematical Theory of Communication" 1948 相互情報量で紹介した伝言ゲームの対称な場合について、通信路容量の曲面を描いてみましょう。
図１ 2値対称モデル（赤を白に誤る確率と白を赤に誤る確率が同じ）
上の式で、右辺第１項と第２項は
とおくと、
のような形をしています。 この関数はエントロピーの説明で頻繁に出現する関数ですが、
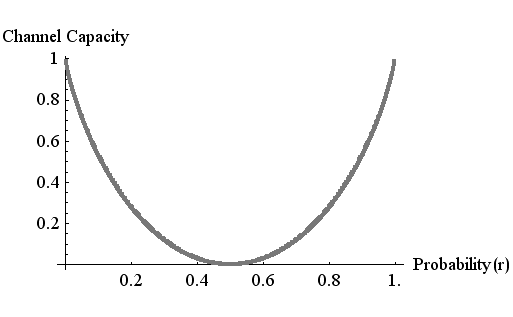
となります。 この結果を描くと下図のような曲線になります。
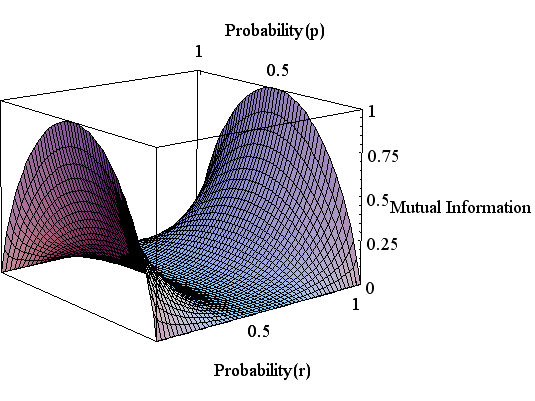
図２ 2値対称チャンネルの通信容量（シャノン限界） この曲線は下図の鞍の形をした相互情報量の尾根をたどる曲線になっています。
図３ 相互情報量の曲面（相互情報量を参照）
以上から、2値対称モデルでは、送信2値シンボルの発生確率が同じとき（p=1/2 ）、通信容量が最大になり、その最大値は誤り率（r ）に依存し、図２のカーブで与えれることが分かりました。図２のカーブは、伝言者が送信データに曖昧さを与えた結果、受信データに含まれる送信データの確からしさの「劣化の度合い」を表しています。 シャノンは、誤りの無いデータ通信を実現するためには、送信データの速度を「劣化の度合い」に等しいレートに落とせばよいと考え、そのような符号化が存在することを証明しました（通信路の符号化 や ディジタル通信の速度限界
を参照）。 このページではディジタル信号について通信容量を求めましたが、アナログ信号に対しても通信路容量を導くことができます。これについては、
アナログ信号のエントロピー
を参照してください。 注： シャノンの理論は、全時間に渡って定常な信号やガウス雑音を前提にしています。ただし、周期定常の環境では、シャノン理論は必ずしも有効ではありません（ロバスト伝送を参照）。 |
を適当に選んで相互情報量を最大化したものはチャンネルが送れる最大の情報量を表します。 この最大値
に依存していますが、第３項は 
に依存していません。 第１項と第２項の和は、
（すなわち 
）のとき最大値１ をとります。 したがって、通信路容量は
のとき通信路容量は情報源に関係なくゼロですが、このことは、伝言者がまったく信用できないとき、いかに情報源を設計しても受信者に情報を伝えることができないことを意味しています。 一方、
のとき通信路容量は１ です。すなわち、正確な伝言者に対しては、送信情報源のエントロピーがそのまま受信信号のエントロピーになります。なお、図３から、対称モデルでは、常に 
のとき、通信路容量を与えることが言えます。