|
(A) 無記憶情報源の場合
サンプル値系列が独立で同じ確率分布に従う
(
I I D :Independent Identically Distributed )としたとき、サンプル値ごとに量子化し(脚注)、憶情報源を拡大して可逆なハフマン符号を適用します。
- 量子化を 8 ビットとすると、サンプル値は256
個の値(シンボル)のどれかで代表される。
- サンプル値の確率密度関数が与えられると、256
個のシンボルの確率が決まる。
- 各シンボルのハフマン符号を求め、その平均符号長を計算する。
- 平均符号長がエントロピーを十分に近似していなければ、情報源を倍に拡大する。すなわち、サンプル値系列を2個づつに区切って、2次元ベクトルが出力されると考える。 ベクトルの個数は
256*256=65536 となり、それらの生起確率はベクトルの各要素の生起確率の積(独立なので)である。
- 65536 個のベクトルに対してハフマン符号を求め、その平均符号長を計算する。
- 平均符号長の半分がまだエントロピーを近似していなければ、情報源を3倍に拡大する。すなわち、サンプル値系列を3つづつ区切って、3次元ベクトルが出力されると考える。ベクトルの個数は
256*256*256=16777216 となり、それらの生起確率を求める。
- 16777216個のベクトルに対してハフマン符号を求め、その平均符号長を計算する。
- 平均符号長の1/3がまだエントロピーを近似していなければ、情報源を4倍に拡大する。すなわち、サンプル値系列を3つづつ区切って、4次元ベクトルが出力されると考える。ベクトルの個数は
256*256*256*256=4294967296 となり、それらの生起確率を求める。
- 以下、同様・・・・・
(B) マルコフ情報源の場合
やはり、信号をサンプルごとに量子化するものとします。 理論的には、マルコフ情報源についても上の手順をそのまま適用できます。 無記憶情報源では、上の手順は急速に真のエントロピーに収束しますが、実用で現れるマルコフ情報源は長いマルコフ性をもつため、上の手順はなかなか収束しません。 マルコフ性が切れるブロック長mは別の方法で決めなければなりませんが、これは情報源に固有であり、一般的手法は存在しません。
たとえば、英文のエントロピー(平均情報量)を求めたシャノンの論文では、まずアルファベット系列のマルコフ性の統計データからエントロピーの計算を進め、それを4次で止めています。 その理由は、第一に英単語の平均長が4.5文字であり、単語の後にはブランクやカンマやピリオドが続くこと。 第二に
Zipf によって発見された英単語の統計的性質があったからです。 Zipf の法則は、単語を頻度の高い順番に並べたとき、単語の出現確率は0.1/n (n は順位)になるというものです(英文のエントロピーを参照)。単語系列のマルコフ性は十分に小さいと思われるので、単語単位のハフマン符号を求めれば、それは限界に近い可逆圧縮符号です。
アナログ信号では、英文のような都合のよいマルコフ性の切れ目は一般に見つかりません。 また、本来は連続的な信号ですから、その扱いはかなり複雑になります。 非常に多くの圧縮法が考案され、実用されていますが、その基本的な部分に焦点を当てて見てみます。
<情報源や受け手の性質を積極的に利用する(分析して合成)>
画像や音楽や音声のアナログ信号をAD変換したものは長いマルコフ性をもつので、直接上の手順を適用するのは無謀です。 まず情報の発生メカニズムや受け手の感覚器官の性質を利用した非可逆圧縮によってハフマン符号の対象を絞り込みます。
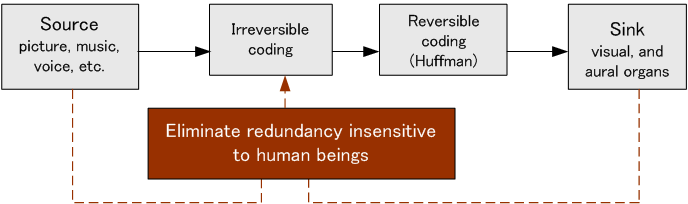
特に音声は、情報源も聞き手も人間であることから、その非可逆圧縮はかなりややこしくなりそうです。 非常に多くの圧縮法が考えられており、詳細は専門書に譲ります。
下図は、22.5KHzでサンプリングした音声波形(50msec)の母音区間と子音区間、そして、約5秒区間の周波数分析のサンプルです。
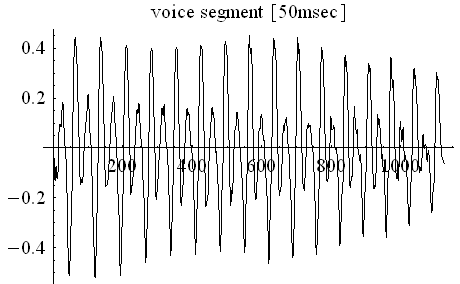
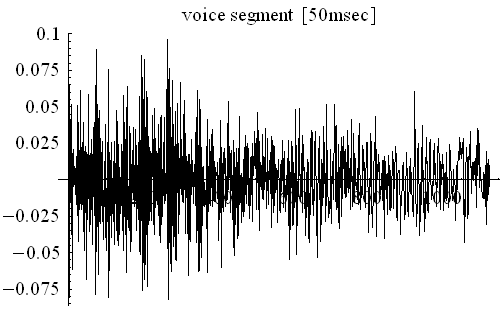
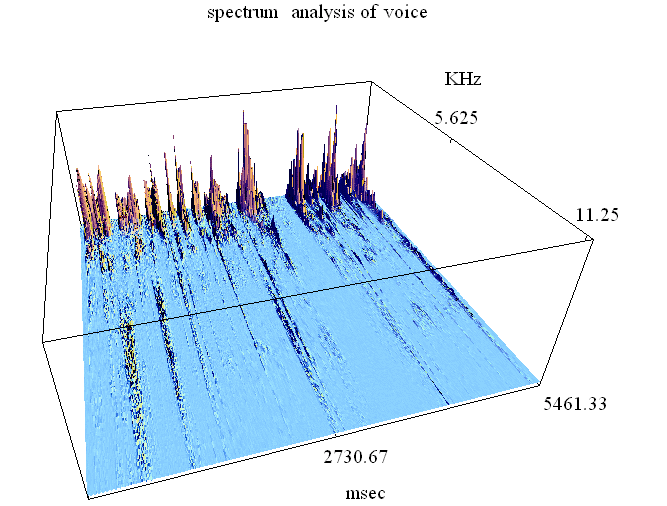
もし、発声メカニズムの音響モデルが出来れば、そこから圧縮の方法を作り出すことができます。ボコーダ(Vocoder)と呼ばれる圧縮方法はこのアプローチから開発されたものです。人間は、声帯を振動させ、その音を声道でフィルタリングして発声しています。 声帯が発する破裂音の繰り返し(ピッチ)は、鋭い三角形をしたスパイク状のパルスの繰り返し(100Hz〜250Hz)です。 このパルスの周波数成分は4KHz以上まで広がっています。スパイクの鋭さやピッチ周波数の変動幅には個人差があり、またアクセントによっても変化します。 声道はその形状を変化させて、共鳴システムを作り出し、スパイク状パルスをフィルタリングして、a,
i, u, e, o の母音を表現します。 したがって、発声機構(有声区間)は、スパイク音源とそのフィルタリングに大別されます。 圧縮は、ピッチ周波数の変化と声道フィルタリングの変化に分けて、特徴抽出して圧縮符号化します。 受信側では、この符号によって音響モデルを制御して再生します。 なお、母音を特徴付ける周波数(フォルマント)は500Hz〜2KHzに分布します。1KHzの音の波長は34cm(空気中の音速は 340m)ですが、これは人間の声道の長さにほぼ等しく、声道で空間を作って音響的に共鳴させることができるわけです。以上の処理は、時間で言えば、1/500Hz=2ms程度のマルコフ性を扱うことになります。
以上は短時間モデル化ですが、実際には上の波形のように、母音区間も子音区間も、比較的長い時間に渡って継続します。また、母音のフィルタリング特性はゆっくりと時間変化し、子音波形の特性も明瞭ではないが、ゆっくりと変化しています。このような変化のマルコフ性は非常に長いことが分かります。
携帯電話(8KHzサンプリング)などでは、多くの音源(声帯や子音源のモデル)のリストを予め用意し、音声から抽出した声道特性にリストの中の音源を入力したときの出力を求め、これと音声の類似度が最も高い音源を選択するという方式をとっています。 その概念を下に示します。
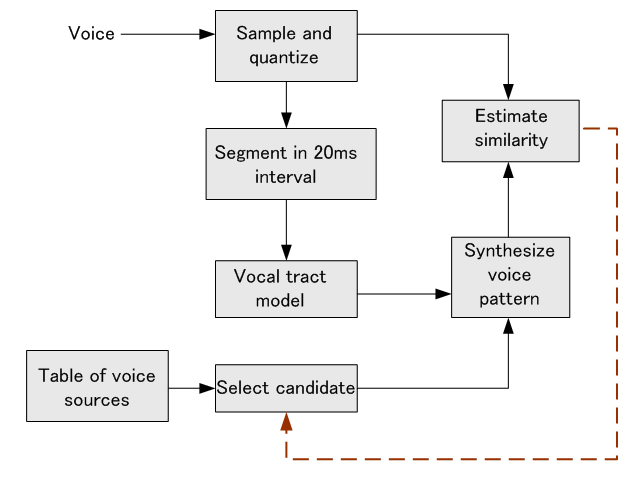
上の図で、声道モデルの変化は長いマルコフ性をもっているので、その推定を切り出した区間内で完結させず、過去の推定から線形予測によって更新します。 これに音源を入力して合成音声を作ります。 この合成音声と実際の音声がどれくらい違って聞こえるかを判定し、許容範囲を越えていれば音源テーブルから別の音源を選択してまたやり直します。 こうして、適切な音源が見つかるまで繰り返します。 この繰り返しは
10ms 内に完結させます。 携帯電話などの音源テーブルには数百の音源が載せられています。 切り出し区間長を16サンプルとし、量子化を8ビットとすると、可能な波形は全部で
 というものすごい数になりますが、そのなかで音源にふさわしいものを数百に厳選しています。 結局、送信するデータは、第一に、声道モデルの推定に関する情報、第二に、選択された音源の番号と音源の強度変化などに関する情報です。 これらの送信データは、ハフマン符号によって可逆圧縮されます。 というものすごい数になりますが、そのなかで音源にふさわしいものを数百に厳選しています。 結局、送信するデータは、第一に、声道モデルの推定に関する情報、第二に、選択された音源の番号と音源の強度変化などに関する情報です。 これらの送信データは、ハフマン符号によって可逆圧縮されます。
<波形の規則性に着目する(適応予測)>
下図の左と右は互いに逆システムです。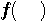 は任意の記憶型非線形関数です。 は任意の記憶型非線形関数です。
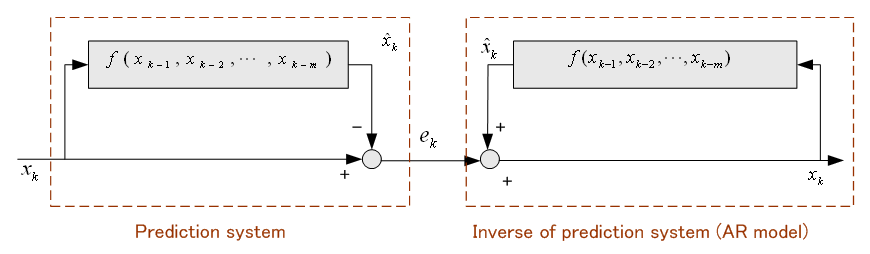
左のシステムは、過去の履歴から今来ようとしている信号 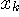 を予測しているとみなせます。 を予測しているとみなせます。 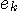 は予測誤差に相当します。 もし、信号 は予測誤差に相当します。 もし、信号 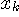 が発生される確率的ルールが時間的に不変(定常)ならば、最適な予測関数 が発生される確率的ルールが時間的に不変(定常)ならば、最適な予測関数 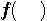 も時間的に固定していいはづです。 しかし、そのルールが時間変化する(非定常)ならば、予測関数を時間的に変化させなければなりません。 たとえば、関数 も時間的に固定していいはづです。 しかし、そのルールが時間変化する(非定常)ならば、予測関数を時間的に変化させなければなりません。 たとえば、関数
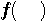 がパラメータで変化するようになっていて、そのパラメータを がパラメータで変化するようになっていて、そのパラメータを 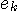 の短時間パワーが小さくなるように常に制御します。 これを適応予測と呼んでいます。 線形適応予測は、関数 の短時間パワーが小さくなるように常に制御します。 これを適応予測と呼んでいます。 線形適応予測は、関数
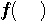 をパラメータ をパラメータ
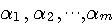 による一次結合とし、予測値を による一次結合とし、予測値を
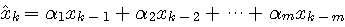
で与えます。そして、予測誤差
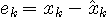
の短時間自乗平均を小さくするようにパラメータ 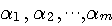 を逐次修正します。 もっとも一般的な、逐次修正の方法は次のようです。 を逐次修正します。 もっとも一般的な、逐次修正の方法は次のようです。
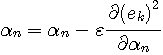
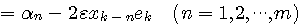
修正係数  を大きくすることは、近い過去の情報ほど重点的に参照しますから、非定常に対する追随能力は高くなります。 そのかわり、予測誤差の揺らぎは大きくなります。 また、信号 を大きくすることは、近い過去の情報ほど重点的に参照しますから、非定常に対する追随能力は高くなります。 そのかわり、予測誤差の揺らぎは大きくなります。 また、信号 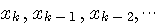 の規則性が強いほど予測誤差の電力を小さくできます。 アナログ情報源のエントロピーでみたように、電力の小さい信号ほどエントロピーは小さいので、予測によって、 の規則性が強いほど予測誤差の電力を小さくできます。 アナログ情報源のエントロピーでみたように、電力の小さい信号ほどエントロピーは小さいので、予測によって、
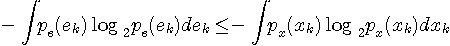
( 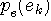 は予測誤差の確率密度関数、 は予測誤差の確率密度関数、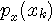 は音声信号の確率密度関数) は音声信号の確率密度関数)
が実現します。 すなわち、予測によってアナログ信号のエントロピーを減少させることができるわけです。 このことをもう少し具体的にみてみます。 8ビットで量子化することは、信号のサンプル値を256個で代表することです。 量子化の直後では、まだ256個には大きな頻度の偏りはありません。 しかし、予測の結果、予測誤差は小さい値に集中します。 すなわち、256個の出現頻度に大きな偏りが生じたことになります。 この確率分布の偏りがハフマン符号による圧縮効果を増大させます。 さらに、予測が完全に遂行されている状態では、予測誤差系列は白色になります。 白色は自己相関がデルタ関数になっていることを意味します。
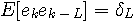 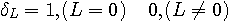
このことは、 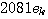 の電力スペクトルが平坦になっていることを意味します。 この性質をもつ系列が予測誤差系列の中に高い確率で含まれるので、これもハフマン符号の効率を上げる材料になります。 予測符号化は可逆ですが、マルコフ性が非常に長いと、一次結合もその長さにする必要があります。 長い一次結合では、非定常性への追随能力が問題となり、これを速くするアルゴリズムの適用が困難になります。 実際には、音声信号に直接的に予測符号化をせずに、分析・合成法の非可逆圧縮の中に組み込む手法をとっています。 の電力スペクトルが平坦になっていることを意味します。 この性質をもつ系列が予測誤差系列の中に高い確率で含まれるので、これもハフマン符号の効率を上げる材料になります。 予測符号化は可逆ですが、マルコフ性が非常に長いと、一次結合もその長さにする必要があります。 長い一次結合では、非定常性への追随能力が問題となり、これを速くするアルゴリズムの適用が困難になります。 実際には、音声信号に直接的に予測符号化をせずに、分析・合成法の非可逆圧縮の中に組み込む手法をとっています。
注: 以上のケースでは、まず信号をサンプル値ごとに量子化して取り込み(スカラー量子化し)、その後で予測符号やハフマン符号などを使って圧縮しました。 しかし、量子化に着目すると、サンプル値列をブロックに区切り、このブロック(ベクトル)を代表ベクトルで量子化すること(ベクトル量子化)が考えられます。 このような量子化装置は大変な気がしますが、もし信号のサンプル値列(アナログ値列)の判定プロセスを階層的に上手く記述できれば回路構成が浮かんできます。 そして、もし信号ベクトルのクラスター分割がRate
Distortion
を最小化するならば、”スカラー量子化+圧縮アルゴリズム”を一挙に実現できることになります。
|







 というものすごい数になりますが、そのなかで音源にふさわしいものを数百に厳選しています。 結局、送信するデータは、第一に、声道モデルの推定に関する情報、第二に、選択された音源の番号と音源の強度変化などに関する情報です。 これらの送信データは、ハフマン符号によって可逆圧縮されます。
というものすごい数になりますが、そのなかで音源にふさわしいものを数百に厳選しています。 結局、送信するデータは、第一に、声道モデルの推定に関する情報、第二に、選択された音源の番号と音源の強度変化などに関する情報です。 これらの送信データは、ハフマン符号によって可逆圧縮されます。
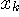 を予測しているとみなせます。
を予測しているとみなせます。 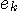 は予測誤差に相当します。 もし、信号
は予測誤差に相当します。 もし、信号 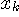 が発生される確率的ルールが時間的に不変(定常)ならば、最適な予測関数
が発生される確率的ルールが時間的に不変(定常)ならば、最適な予測関数 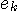 の短時間パワーが小さくなるように常に制御します。 これを適応予測と呼んでいます。 線形適応予測は、関数
の短時間パワーが小さくなるように常に制御します。 これを適応予測と呼んでいます。 線形適応予測は、関数
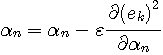
 の規則性が強いほど予測誤差の電力を小さくできます。
の規則性が強いほど予測誤差の電力を小さくできます。