|
ハフマン符号 Huffman code |
|
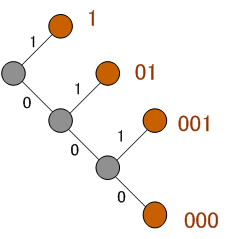
ハフマン符号は情報圧縮における可逆符号(正確に復号できる符号)です。 画像や音声の情報圧縮では、まず非可逆圧縮を行い、残った規則的な(人間が理解可能な)対象に対して、可逆符号による圧縮を実施します(情報圧縮を参照)。 無記憶情報源のいかなる復号可能符号の平均符号長も、その情報源のエントロピー以下にすることはできないことは符号とエントロピーで説明しました。 では、復号可能な符号のなかで、 その符号は、瞬時復号可能な符号の中から見つかり、ハフマン (David.A.Huffman, 1925-1999) がその設計法を示しました。 どの符号語も他の符号語の接頭語になっていない符号は瞬時的に復号可能です。 このような符号は、視覚的に分かりやすい構造をもっています。 下図のように、2本の枝分かれを繰り返す木グラフ(tree graph)を見てください。 左端の根っこから、2本の分枝に“0”と“1”のビットを割り付けてゆきます。 そして、図のように枝の先端(右端の行き止まり)に符号語を割り付けてみます。 符号語は、根っこからその先端まで、枝のビット(0 か1 )を順々に読み取ったものです。 このような符号語の集まりは、互いに接頭語になっていません。 すなわち、かならず瞬時復号可能です。
先端の符号語は根っこに近ければ近いほど符号長が短いので、できるだけ根っこに近いところで符号を割り付ければ能率の良い(平均符号長の短い)符号が設計できます。 もう少し具体的な例を設計してみましょう。 4つのアルファベット(A、B、C、D)を出力する無記憶情報源を考えてください。 それらの出現確率を
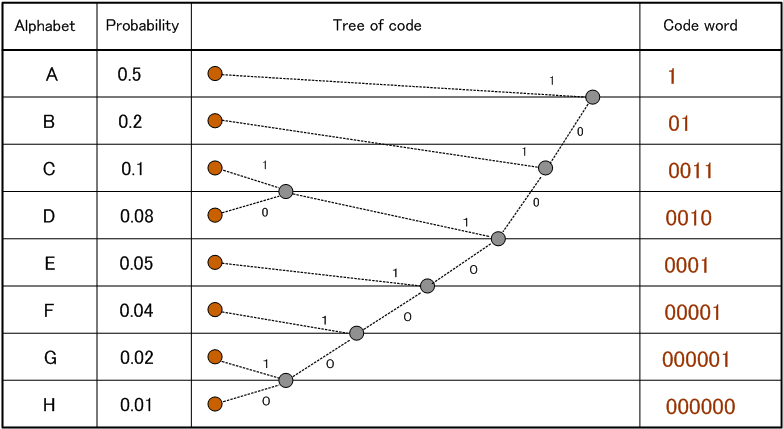
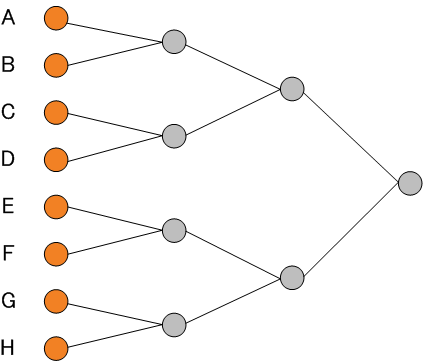
で与えられます。 ハフマンは、アルファベットとその出現確率が与えられたとき、もっとも平均符号長の短い瞬時復号可能符号の設計法を見つけました。 その方法を8つのアルファベットを出力する無記憶情報源で説明します。 下図を参照しながら、アルゴリズムをたどってみてください。左端(2分岐木グラフの端点)から右へ、合流操作を行います。
この手順によって作られた符号は瞬時復号可能になっていますが、実は非瞬時・瞬時を意識しないでも、このようにして作った符号の平均符号長は最短になっていることがいえるのです。 一般に復号可能な最短の符号をコンパクトであるといいますが、ハフマン符号はコンパクトなのです。 その理由は以下のように考えてみれば、すぐに分かります。 二つのアルファベットを合流するということは、そのどちらが発生しても一つの新しいアルファベットとして読むということですから、アルファベットが一つ減ります。合流にともない、符号長も1ビット減るので、平均符号長はそれぞれのアルファベットの確率を
上の例題を8つの会社を二つずつ合併してゆき、最後に一つの会社に統合する問題に置き換えて考えてみます。 合併によって合併損が生じ、全部を統合し終えたときに、合併損のトータルが最小になるようにしたいのです。 合併したときに出す損を確率の値とし、たとえばA社とB社を合併すると、それらの確率の和
0.5+0.2=0.7 なる損を発生するとします。 その結果、合併損 0.7
をもつ新会社と、合併しなかった会社6つ、あわせて7つの会社が残ります。 これら7社から、また二つを選んで合併し、新会社を作ってゆきます。 どのような順序で合併しても、統合が終わるまでの合併の回数はちょうど7回です。 ただし、合併損のトータルは合併の順序によって異なります。下の例を見てください。 合併劇(1):トーナメント試合のように合併する。 A+B=0.5+0.2=0.7 C+D=0.1+0.08=0.18 E+F=0.05+0.04=0.09 G+H=0.02+0.01=0.03 (A+B)+(C+D) =0.7+0.18=0.88 (E+F)+(G+H) =0.09+0.03=0.12 ((A+B)+(C+D))+((E+F)+(G+H)) =0.88+0.12=1.0 トータル合併損(平均符号長) =0.7+0.18+0.09+0.03+0.88+0.12+1.0= 3 合併劇(2):ハフマンの手順にしたがった場合 H+G=0.02+0.01=0.03 (H+G)+F =0.03+0.04=0.07 ((H+G)+F)+E =0.07+0.05=0.12 C+D =0.1+0.08=0.18 ((((H+G)+F)+E)+(C+D) =0.12+0.18=0.3 ((((H+G)+F)+E)+(C+D))+B=0.3+0.2=0.5 (((((H+G)+F)+E)+(C+D)+B)+A =0.5+0.5=1.0 トータル合併損(平均符号長)=0.03+0.07+0.12+0.18+0.3+0.5+1.0= 2.2 この例から分かるように、早めに合併損の小さな2社を選んで合併すれば、トータル合併損を最小にできます。 すなわち、A社に着目すると、A社が関わる合併の度にA社の確率がカウントされます。 したがって、A社の確率が大きいとき、A社が関わる合併の回数をできるだけ少なくする方が得策なわけです。 A社が関わる合併の回数はアルファベットA の符号長に相当しますから、合併劇のトータル合併損はまさに平均符号長に等しいわけです。 以上の符号化では、アルファベットごとにハフマン符号を割り付けました。 この平均符号長はまだエントロピーの限界に達していません。 上で得られたハフマン符号の平均符号長は 2.2 ビットです。 一方、この情報源のエントロピーは 2.17 ビットです。 両者の差は 0.03 ビットです。 この差をさらに縮めるには、情報源を拡大してハフマン符号を作ってゆきます。 たとえば、2次拡大情報源 (2文字綴りを出力すると見做す)のシンボルは、AA、AB,…、HH の全部で64 個です。 これら2文字綴りの出現確率はそれぞれ、
で計算されます。 このように拡大された情報源に対して、ハフマン符号を設計すると、その平均符号長はさらにエントロピーに近くなることがいえます。 そして、この拡大をどんどん行ってゆくと、最後にはエントロピーに無限に近い符号を作ることができます。 このことを保証する事実は、第1に、次の定理が成り立つこと、 定理 注1: i
番目のアルファベットの生起確率を 第2に、次の定理が成り立つこと、 定理 注2: 0と1を出力する2元情報源を考える。 生起確率を
から導くことができます。 すなわち、n次拡大の平均符号長
を満たす瞬時復号可能な符号がかならず存在することがいえ、その中でハフマン符号がもっとも良い(コンパクトな)符号になっています。 このように、n
を大きくしてハフマン符号を設計すれば、元の情報源の1アルファベット当りの平均符号長
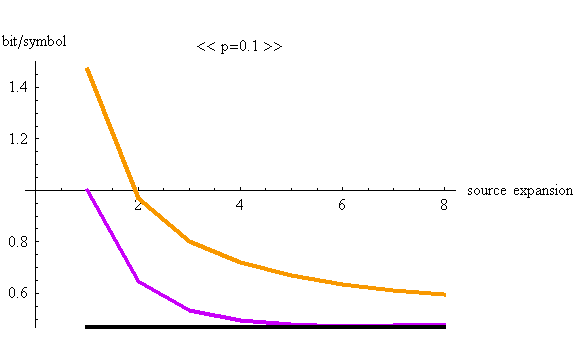
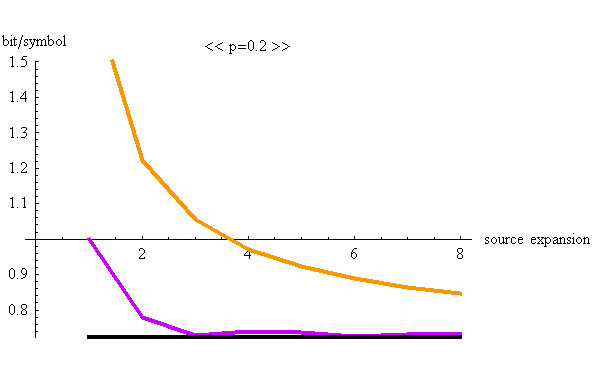
実際に2値無記憶情報源を拡大してハフマン符号を設計し、上の不等式を構成する3つの項をプロットしてみよう。 二つのシンボル”1”と”0”が出力されるとし、”0”の生起確率が
p=0.1 と p=0.2 の場合についてプロットしてみます。 黒が
注3: 上の図から分かるように、ハフマン符号の圧縮率(ビット/シンボル)は、情報源の拡大に対して単調減少とは限りません。 注4: 音声や画像などの圧縮では、ハフマンを適用する前に、聴覚や視覚の特性を利用した不可逆圧縮を実行しています。その理由は、最初から音声にハフマンを適用しようとすると、PCM信号(8KHzサンプリングで8ビットADC)を10ミリ秒ごとに切り取って処理するとして、のサンプル数=80、量子化レベル数=256、なので、符号語の数は256の80乗という膨大な数になります。というわけで、符号語数を音声の特徴を使って減らそうというわけです。不可逆圧縮によって残った符号語のエントロピーが大きい(規則性が小さい)と、ハフマンの圧縮効果は小さくなり、逆に小さい(規則性が大きい)と、ハフマンの圧縮効果は大きくなります。聴覚や視覚の特徴を当てにしないで、符号語をクラス分けして、階層的なハフマン符号を構成することができないのかなー?と疑問に思っていますが、私は専門ではないので、これ以上のコメントはできません。 |
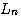 が
が