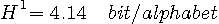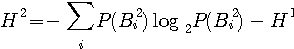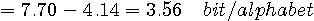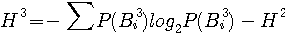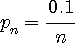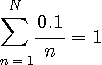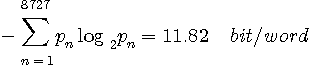|
英文のエントロピー Entropy of English language |
|
情報源のエントロピーは1940年代にシャノン(C.E.Shannon)によってはじめて定義されました。 シャノンは、論文("Prediction and Entropy of Printed English", The Bell System Technical Journal, January 1951)で英文のエントロピーを計算しています。 まず、アルファベットのマルコフ性(アルファベットの順序分布)を利用してエントロピーの計算を進め、それには限界があることを述べ、次に単語の頻度分布に Zipf の法則があることを利用して、英文を”単語を無記憶に発生する情報源”と見做したときのエントロピーを求めています。 英単語の平均アルファベット数は4.5文字なので、それを4.5で割ればアルファベット当たりのエントロピーが得られます。以下に、シャノンの論文の前半部分を要約します。 注:実際には、単語間にもマルコフ性があります。 このマルコフ性を直接的に求めようとすると、仮に英語を1万語の単純マルコフとしても、2単語の並びの個数は1万×1万=1億になってしまいます。 有効な統計を得るには、1億の数百倍の統計量が必要ですから気が遠くなってしまう! 英文をm重マルコフ情報源とみた場合のエントロピーは次のように計算できます。 マルコフ情報源のページでは、m文字綴りを単位として、この間の確率的遷移でマルコフ情報源を記述しました。 まずは、この記述にしたがうエントロピーの計算式は次のようです。
右辺2番目の総和は、 i 番目のm文字綴り(
が与えられます。 これを上のエントロピーの式に代入して、
が得られます。 ここで右辺2番目の総和の項数はアルファベットの数と同じです。 しかし、シャノンは当時、英文の遷移確率
で表わせます。 したがって、
を上のエントロピーの式に代入して、
が得られます。 まず、マルコフ性およびアルファべットの出現確率をまったく考慮しないで、単に26個のアルファベット(大文字と小文字を区別せず、スペースやカンマやピリオドなども考慮に入れないで)がランダムかつ等確率で出現するとすれば、エントロピーは
になります。 これは英文の最大エントロピーです。 次に、1次近似は、一つのアルファベットの出現頻度の偏りを考慮し、
によって計算します。 アメリカでは、Blue Ribbon Books という公文書にアルファベットやブロック
となります。 続けて、2次近似は
となり、 3次近似は
となります。 数学的には、この計算をどんどん続けてゆけば、限りなく英文のエントロピーを近似するわけですが、シャノンはこの計算をここで止めています。 その理由は、英単語の平均語長が4.5文字であり、3次以降では単語間のスペースの影響がでてきて、この近似では実際の英文を反映しなくなるからです。 そこで、シャノンは方針を変え、単語に着目しました。 単語の出現頻度に関して G. K .Zipf がが注目すべき法則を発見していました。 その内容は、英単語の頻度分布には次のような美しい関係があるというものです。 英単語でもっとも頻出するのは the、次はof です。 Zipf は、英単語を、the、of、and、to のように頻度順に並べると、順位 n の単語の確率は
で近似できることを発見しました(統計例)。 確率は総和をとると 1 にならなければならないので、この近似が有効な順位は
を満たすNまでです。Nを計算すると8727 となります。 情報源が8727 個の単語を上のような頻度で無記憶に出力するとみて、エントロピーを計算すると、
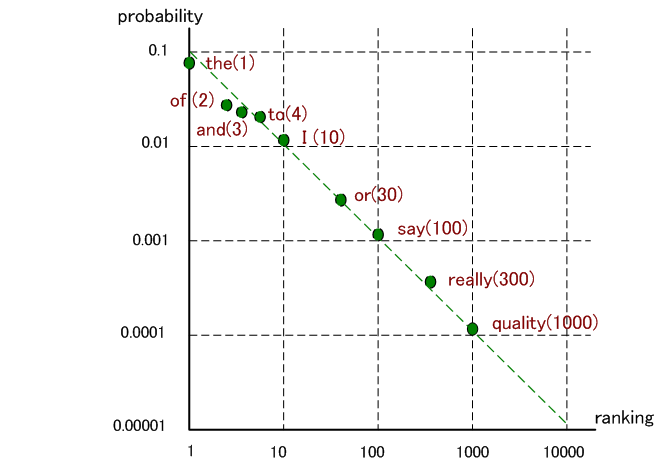
となります。 ワード数が1000の英文は、平均的に言って、長さ11820の2値(0または1)系列に符号化できることを意味しています。具体的には、単語に対してハフマン符号を設計することになる。 なお、アルファベット単位に換算すると、単語の平均文字数 4.5 で割って、 11.82/4.5=2.62 ビット/alphabet になります。 Zipf の法則は、単語の頻度がその順位に反比例することを意味しています。 このことは、大変不思議な気がします。 両辺の対数をとると、単語は直線上にプロットされることになりますが、下のように、みごとに直線上に乗っています。
Zipf はこの原理が言語や都市の人口など、いろんな統計に対して成り立っていることを著書 “Human Behavior and the Principle of Least Effort” Addison-Wiley Press, 1949 で主張しています。 この論文のタイトルから、なにか哲学的な内容を感じますね。 深みにハマリそう・・・・。 Wikipedia日本語版、あるは、Wikipedia英語版 などを参照してください。
|
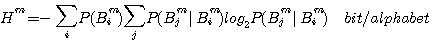
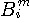 )をすでに知った後で、次に一つのアルファベットを受けて新たな綴りに遷移したことを知ったときのエントロピーを意味しています。 右辺1番目の総和は、このエントロピーをすべての綴りの頻度で平均することを意味しています。 このm文字綴り間の遷移による表現は、
m文字綴りの次に
j 番目のアルファベット
)をすでに知った後で、次に一つのアルファベットを受けて新たな綴りに遷移したことを知ったときのエントロピーを意味しています。 右辺1番目の総和は、このエントロピーをすべての綴りの頻度で平均することを意味しています。 このm文字綴り間の遷移による表現は、
m文字綴りの次に
j 番目のアルファベット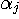 を受けたとして表現することもできます。 まず、m文字綴り
を受けたとして表現することもできます。 まず、m文字綴り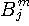 の中で、
の中で、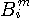 から遷移不能なものがいっぱいあり、それらの遷移確率はゼロですから、非ゼロのものに着目すると、
から遷移不能なものがいっぱいあり、それらの遷移確率はゼロですから、非ゼロのものに着目すると、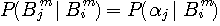
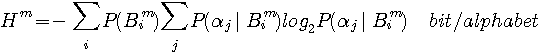
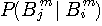 あるいは
あるいは 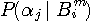 に関する統計データを入手することはできませんでした。 入手できたのは綴りの頻度でした。 そこで、シャノンは次の漸化式で計算しようと試みました。 一般に、同時確率
に関する統計データを入手することはできませんでした。 入手できたのは綴りの頻度でした。 そこで、シャノンは次の漸化式で計算しようと試みました。 一般に、同時確率 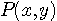 は、
は、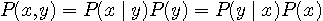
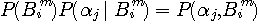
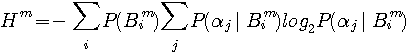
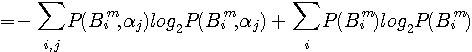
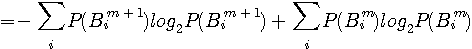
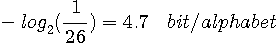
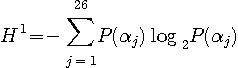
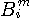 の頻度データが載っています。 これを使って上式を計算すると、
の頻度データが載っています。 これを使って上式を計算すると、