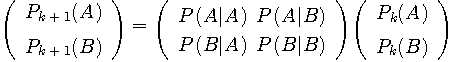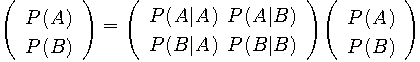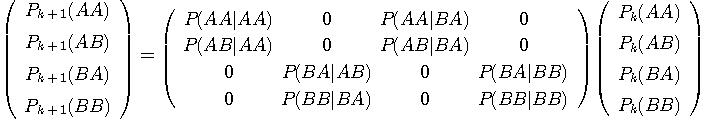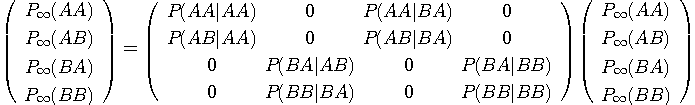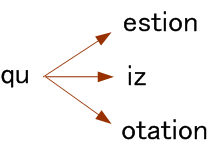
英語の綴りを例にとると、過去に出現したアルファベットに依存して、いま出現するアルファベットの確率が決まります。　このような情報源をマルコフ (Andrei Andreyevich Markov, 1856-1922) 情報源といいます。　現実の情報源は、ほとんどがマルコフ情報源です。　たとえば、英文では Q の次には確実に U が、そして QU の次には母音 E や I や O が出現しやすいのです。

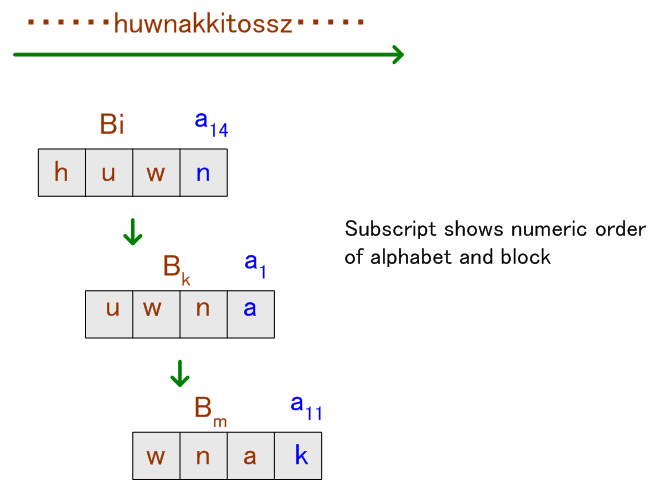
このようなマルコフ情報源をどのようにモデル化すればよいかを考えてみましょう。

直前のｍ個のアルファベットからなる綴りをｍ次ブロックと呼ぶことにします。　英語ならば、アルファベットの個数は２６ですから、ｍ次ブロック、すなわち長さｍ の可能な綴りは全部で 個です。　各ブロックに番号 i を付けて、それを と書きます。　すると、ブロックの次に来るアルファベットの出現確率が条件付確率

で表されます。　ここで、 は ｊ 番目のアルファベットを表します。 ｊ 番目のアルファベットを受けると、次のブロックは、先頭が で、その後にブロック の先頭から ｍ−１番目までの綴りが続くブロックへ遷移します。　このようにして、マルコフ情報源はブロックからブロックへ確率的に遷移するモデルで表現できます。　すなわち、 は で表現していいわけです。

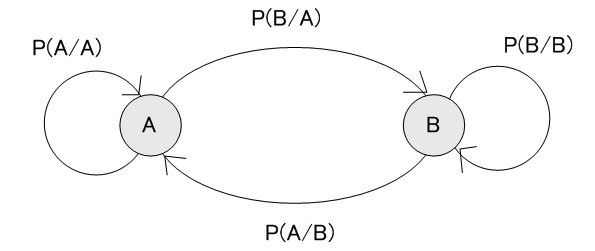
もし、ブロックの長さが１ ならば、 は一つのアルファベットから一つのアルファベットへの遷移確率であり、アルファベットの出現は一つ前のアルファベットのみに依存することになります。　このような情報源を単純マルコフ情報源と呼んでいます。　ブロック長がｍ ならば、ｍ重マルコフ情報源といいます。　マルコフ情報源の性質を調べるために、簡単な例で話を進めましょう。　もっとも簡単なものは単純マルコフ情報源です。　この場合、遷移図は下のようになります。　

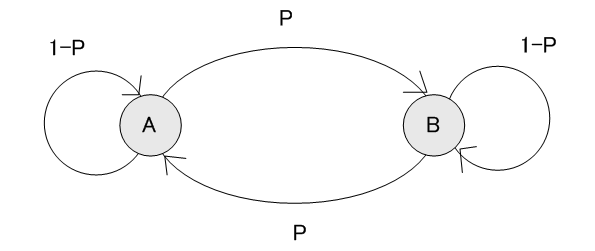
上の遷移図は、時刻ｋでのAとBの出現確率 , が次の時刻では

によって与えられることを表しています。 定常状態では、AとBの発生確率は永遠に時間が経つと一定になると考えられますから、この情報源から出力されるAとBの頻度（定常確率）を で表すと下の連立方程式を満たすはずです。

仮に、遷移が対称ならば、遷移図は

のように表され、このときの定常確率は

を解いて、

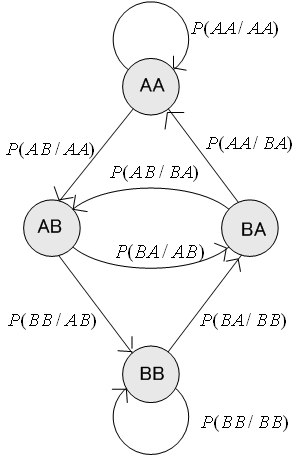
となります。　今度は、２重マルコフ情報源について、もう少し一般的に考えをたどってみましょう。　ブロックは、AA、AB、BA、BB の４通りです。遷移確率は 、 などの条件付確率で与えられます。　ブロックからブロックへの遷移は下図のように表されます。

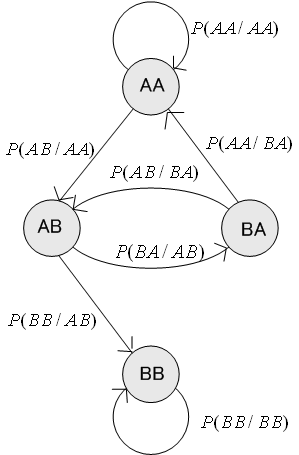
もし、すべての遷移確率が非ゼロならば、この遷移に沿って移動すると、どのブロックにもいつかは到達できます。　しかし、もし

ならば、下図のように、いったんブロック BB に入ると、永遠に BB から抜け出すことはできません。　

どのブロックからスタートしても、任意のブロックへ遷移可能なケースを「エルゴード的」といいます。　我々が扱うマルコフ情報源の多くはエルゴード的です。　もし、エルゴードでなければ、エルゴードな部分に分割して考えることになります。

注：　アルファベットの個数が多く、その間の遷移（枝）も複雑な場合、エルゴード部分の分離は非常に難解な問題（グラフ理論における、閉グラフ抽出の問題）になります。

もし、ブロック AA からスタートすると、次は AA または AB に遷移します。その確率は、  と です。　この双六（スゴロク）のようなゲームを十分長く繰り返すと、各ブロックを通過する頻度を計測することができます。　このようにして具体的に計測した頻度は、各ブロックの出現確率 、、、 を表しています。　英語では２文字綴りの出現頻度に相当します。　では、このブロックの出現確率を、双六ゲームを実際に行わないで求めるにはどうすればよいでしょうか？　「振り出し」は AA でした。振り出しが AA に確定しているということは、

ということです。　次に遷移する先は AA または AB ですが、その確率は  と で与えられます。　したがって、最初の遷移によるブロックの出現確率は

のようになります。　以下、サイコロを振るたびに、ブロックの出現確率は下の漸化式にしたがって変化します。

もし情報源がエルゴード的ならば、この遷移を無限に繰り返すと、ブロック AA、AB、BA、BB が出現する確率は一定の値に収束します。　言いかえれば、双六の上を十分長い時間さまよった後では、振りだしのブロックに関係せず、各ブロックを通過する頻度が一定の値に落ち着いてしまうということです。　この状態のことを定常状態といい、このときの確率をブロックの定常確率といいます。上の漸化式を無限に繰り返すと、実は一意な定常確率に収束することがいえます。　したがって、定常確率は

を満たすはずです。　この連立一次方程式を

の条件下で解けば、定常確率を求めることができます。

ブロック長 m を大きくしていくと、ブロック間の確率的相関が希薄になり、結果として、長さ m のブロックを出力する無記憶情報源に近づきます。このとき、無記憶情報源を前提とした可逆な（複合可能な）圧縮符号がそのままマルコフ情報源にも適用できます（可逆符号化を参照）。

言語は典型的なマルコフ情報源ですが、膨大な統計データの処理になります。シャノンは英文のエントロピーを求める論文を書いていますが、そこでは、上述のような煩雑な手順を英文に当てはめることの大変さと精度に疑問をもち、英文を単語の無記憶情報源と見做して計算しています。英文のエントロピーを参照してください。