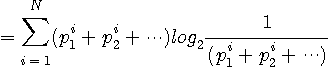|
Rate Distortion |
|
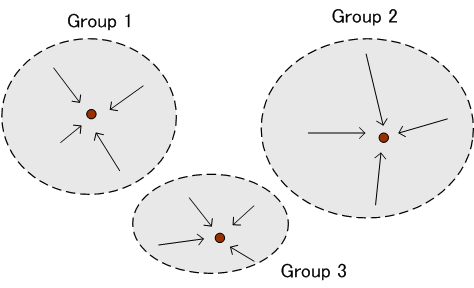
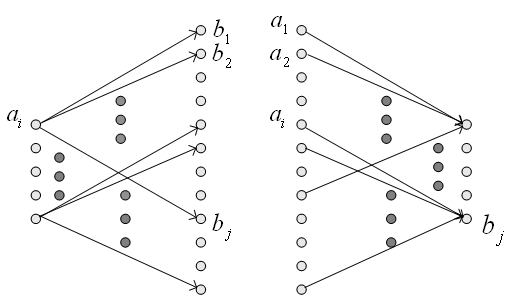
下図は、左側の信号が右側の信号に確率的に変換される様子を表しています。 実際には、信号
とします。
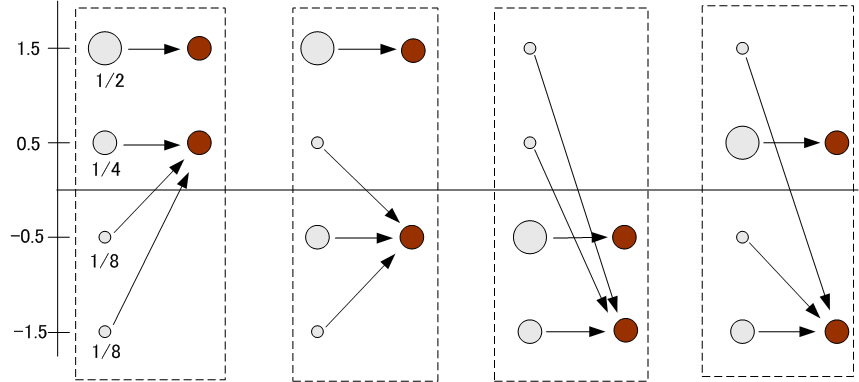
図１ 信号変換 左と右の信号の個数は同じであり、各枝には条件付き確率
図２ 通信モデル（左）と非可逆圧縮モデル（右） さて、図１で、左側が送信信号、右側が送信信号の判定結果とみなせば通信モデルです。 チャンネルが透明で判定に誤りがないとき、条件付き確率は
を満たしています。このとき、送信情報は損失なしに受信されます。 言い換えれば、送信側のエントロピーと受信側のエントロピーは等しいはずです。 さらに言い換えれば、 送信エントロピー ＝ 相互情報量 が成り立っています。相互情報量は、受信信号に送信信号の情報がどれだけ含まれているかを測る尺度です。 雑音があれば、一般に
となり、相互情報量は送信エントロピーよりも小さくなります。 条件付き確率によって送信信号が分散する様子を想像すると、次のような傾向がありそうです。 送信信号の確率分布が与えられたとして、 この傾向を厳密に分析するのが Rate Distortion 理論です。 まず、「受信信号の広がり」という言葉を具体的に定義しなければなりませんが、この定義には次の３つが関わります。
ここで、「距離」は距離の公理、
を満たしている必要があります。 たとえば、信号が電圧で表されるとき、
ですが、これも距離の公理を満たしています。 距離の定め方は無限にあります。 「信号の広がり」を、送信信号と受信信号の距離の平均で測り、それを Distortion と呼びます。
上式は条件付き確率
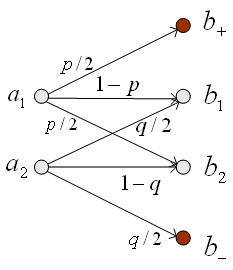
を結びつけようとするものです。 それでは、 送信信号の確率分布が与えられたとして、 平均距離を一定にしても、条件付き確率にはまだ大きな自由度が残っていますから、明らかに一意には決まりません。 われわれの興味はこの上限（最良）と下限（最悪）がどうなっているかに移ります。 Rate Distortion は相互情報量の下限を与えるものです。 このことは、送信信号の確率分布を固定して、チャンネル（条件付き確率）の広がり具合を与えて、そのときの最悪な情報伝送能力を求めています。 この双対、すなわち条件付き確率を固定して、送信信号の最良な確率分布を求める問題は通信路容量でした。 さて、Rate Distortion がどのように応用されるかを問題にしなければなりませんが、その前に、簡単な例題でこの問題の直感を養いましょう。 図３は、２値送信信号に雑音（加法的とは限らない）が加わり、判定誤りを起こす通信モデルです。
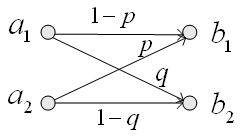
図３ ２値通信モデル 送信シンボル
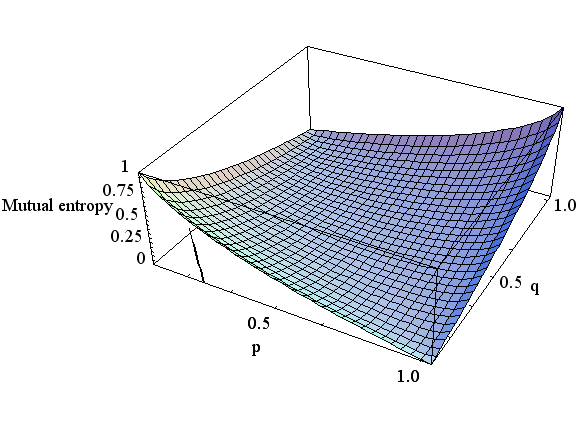
図４ 相互情報量 送信シンボルの生起確率に偏りがあり、 それぞれを1-r と r とし、シンボル間距離を１とします。 送信信号と受信信号の差の絶対値を距離と定義すると、平均距離は
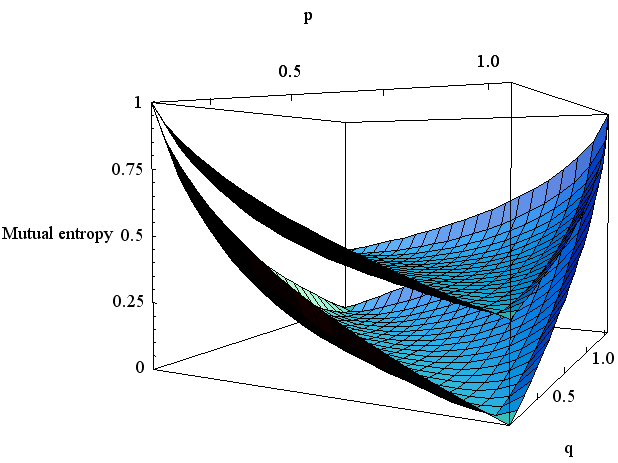
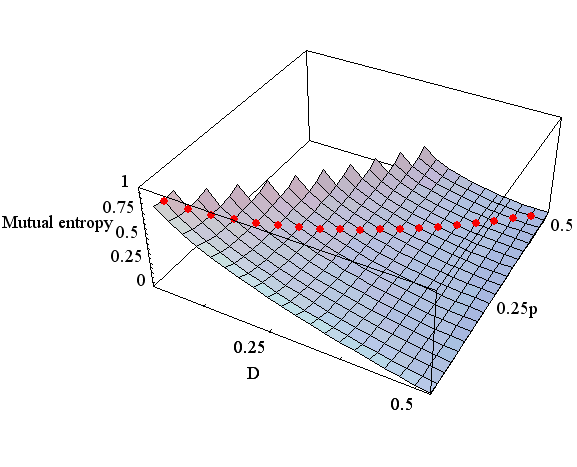
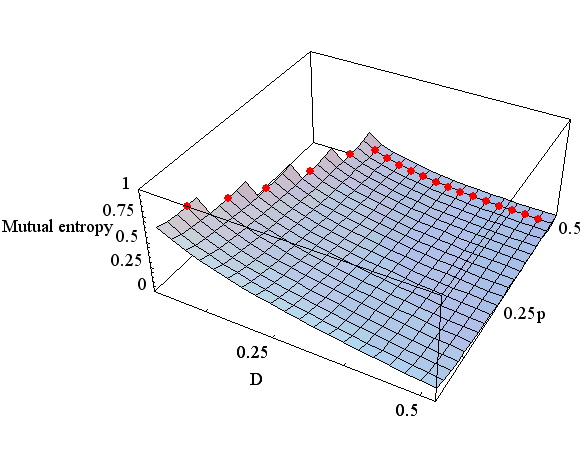
で与えられます。 したがって、r が与えられた状態で、平均距離を一定とすると p と q は底面に引かれた描かれた太い線分上に拘束されます。 Rate Distortion はこの線分の真上の曲線の最小点に当たります。 D が増加すると線分は原点から遠ざかり、この最小点は単調に減少し、しかも減少速度はだんだん小さくなっていくことが想像できます。 実際、p と D を変数とする相互情報量を描くと図５のようになります。図５は、0<p<0.5, 0<D<0.5 の範囲で描かれています。 曲面の無い部分は q が負になる場合です。 赤い点線は、D を固定しながら p を変えて最小を求めた解であり、Rate Distortion を表しています。
図５ Rate Distortion （上は r=0.5、下は r=0.25） ２値以上の送信信号に対する一般論は次のことを結論しています。 Distortion を拘束したときの相互情報量の したがって、Rate Distortion の意味を次のようにまとめることができます。 多くの場合、送信信号の統計的性質を固定し、 ついでに、D を固定して、送信信号とチャンネルの両方を変化させてみましょう。 p
を与えると q が決まるので、独立変数は r と
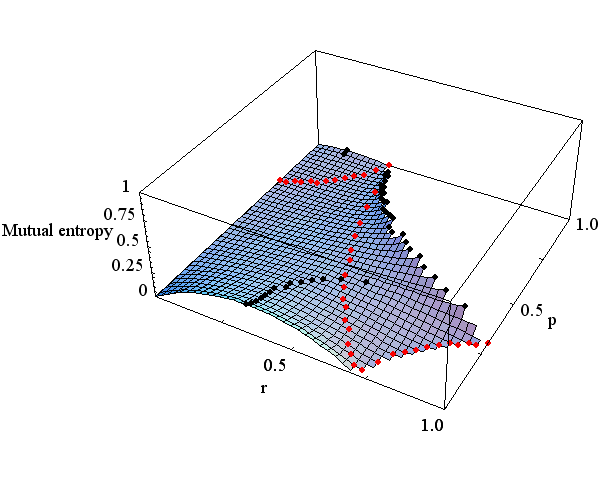
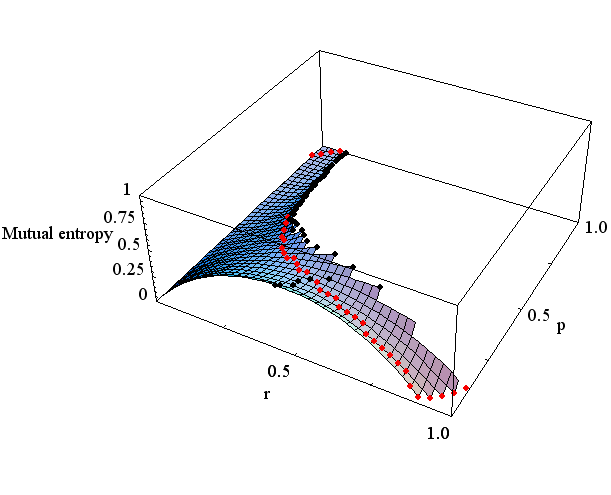
p です。図６は、 D=0.3 と D=0.1 のときの相互情報量
図６ 上はD=0.1 下は D=0.3 この曲面をよく見ると馬の鞍の形をしています。 すなわち、p を固定して r を変えると上に凸、r を固定して p を変えると下に凸になっています。 図６に描かれた黒色の点線は尾根筋、赤色の点線は谷筋を表しており、それぞれ
で与えられます。 さらに、２本の道が交叉する点は峠(Saddle Point)
を表しています。 尾根筋は、チャンネル（条件付き確率）を与えて相互情報量を最大にするような送信源を求めていますから、通信路容量に相当します。 谷筋は、送信源を与えて相互情報量を最小にするチャンネルを求めていますから、Rate Distortion です。 したがて、 ある Distortion を与えるチャンネルは無数にある。 D を大きくすると、谷筋は全体的に下がってきます。 したがって、谷筋の最高点（峠）も単調に下がることが予想されます。 受信信号の Distortion を計測するだけで、 さて、冒頭の図２左側に戻りましょう。 図７はもっとも簡単なモデルです。 雑音によって広がった２値信号を４値量子化しています。 この結果を正負判定すれば図３のモデルになります。
図７ 受信信号の量子化モデル 図７の茶色で示した両端の信号を受信したとき、その判定は必ず正確です。 したがって、このケースでは、相互情報量はゼロになることはありません。 実際、図４の上に、この場合の相互情報量を重ねて表示すると、図８のようになり、常に図４の曲面の上に位置します。 このことは、信号数の多い場合にも一般に成り立ちます。 この場合の Rate Distortion はこれまでと同じストーリーをたどれば済みます。
図８ 図３と７の相互情報量の比較 注１： なお、図８の結果は、判定（このような閾値判定を硬判定という）してしまうと、相互情報量が減少することを示しています。 この事実から、硬判定を急がずに、４値の量子化結果の時系列をひとまず記録して、系列として判定を行う方が有利であることを示唆しています。 このようなテクニックを軟判定と呼んでおり、誤り訂正符号と組み合わせて、通信の信頼性を向上させる有効な方法です。 最後に図２右側の圧縮モデルに関して、Rate Distortion を検討します。 典型的かつ実際的な例として、図９のようなモデルを調べてみましょう。 図９では、クラスターが分離して代表パターンに収縮しています。したがって、すべての枝の条件付き確率は１であることに注意してください。
図９ 硬判定モデル まず、Distortion を考慮しないで、次の問題はどうなるでしょうか？ 情報源信号を N 個のクラスターに分類し、 上でいう「分類」は、通信モデルにおいて条件付き確率を変数としたことに相当しています。 また、「その中の一つで代表する」はこの段階ではまだ
Distortion を考慮していないので関係はありません。 i 番目のクラスターの信号とその生起確率を
相互情報量 この形から、クラスターの確率の総和が均等になるように分類すれば、相互情報量が大きくなることが分かります。 逆に、相互情報量を小さくするには、クラスターの確率の総和に大きな偏りをもたせればよいこともいえます。 いずれにしても、上の問題では、Distortion はまだ関与していません。 では、 簡単な例題でみてみましょう。 ４つの信号の生起確率を
とし、これを２分割します。 相互情報量を最大にする分割は クラスター１ クラスター２ です。 このクラスタリングを満たす信号値の並びはいろいろありますが、下図はその例です。
図１０ クラスタリングの例 右の二つは、クラスターが他のクラスターを跨いでいるため、圧縮として適切な分類ではありません。 以上から、単に相互情報量を大きくするだけでは、人間の認識・認知に貢献する結果は得られないことが分かります。 たとえば、音声の有限区間サンプリング系列の電力スペクトルは、それが音声であるということから大きな確率的偏りをもち、かつ自然にクラスタリングされていると考えるべきです。 このような場合においては、スペクトル間距離を問題にして分類した方がよさそうです。 すなわち、各クラスター毎に、代表スペクトルからの平均距離を求め、それらの和をもって Distortion とします。 そして、この Distortion を最小にするようにスペクトルを分類して圧縮します。 距離が定義されたパターン空間に、パターンが確率的に発生する。
注２： 実際的なケースでは、最小 Distortion の近傍には多くのクラスタリングが存在します。 これらの相互情報量の上限と下限の幅は狭くなっており、クラスター内の確率の総和がバランスする傾向をもっています。 この中で、もっともバランスしているものが最大の平均相互情報量を与えますが、これを選択することが非可逆圧縮においてどのような意味をもつかは興味深い問題です。 注３： Rate
distortion function を求めるアルゴリズムは下記を参照。 |
や 
は数値やベクトルや符号などであり、ここでは、番号が同じならば、
（ 
から 
に変換される確率）が割り付けられています。 Rate Distortion 理論では、すべての条件付き確率を独立変数としています。 しかし、実際の応用では、これらの間に従属関係があったり、特定のグループがゼロであったりします。 たとえば、図２左側は信号が分散するケースを表し、右側は信号が収縮するケースを表しています。 前者は信号が雑音などで分散する伝送モデル、後者は多くのパターンを少数のパターンで代表する情報圧縮モデルとみてもいいでしょう。
（ 
ならば 
）
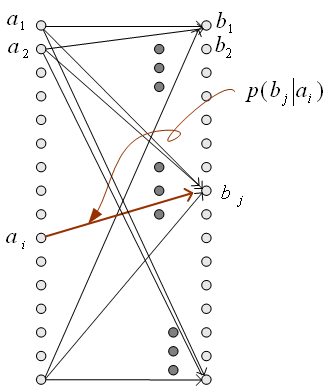
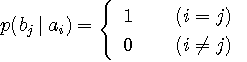
は信号 
と信号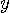 
の電圧差ですが、これは距離の公理を満たしています。 また、判定誤りは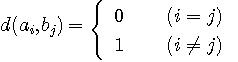
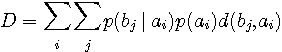
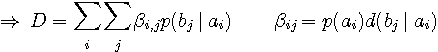
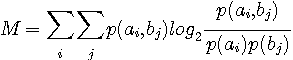
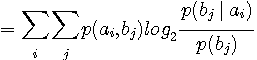
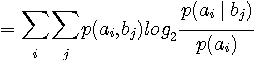
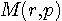の一次結合の形をしています。 このことは、これを拘束条件とする変分法（評価関数の最大（小)を求める方法）を解くために重要です。 Rate Distortion はこの平均距離と次の相互情報量
と 
の生起確率が等しい場合について、条件付き確率 p と q を変化させたときの相互情報量を描くと、図４のようになります。 曲面は柔らかい方形板の端を両手で持ち上げたような形をしていて、下に凸です。
そして、底辺は床に接しています。
, 
を描いたものです。 0<r<1, 0<p<1 の範囲で描いています。 曲面が欠けているところは、値が定まらない
(qが負になる）領域です。
と 
および 
で表すと、相互情報量は次のように簡単な形になります。 
