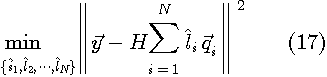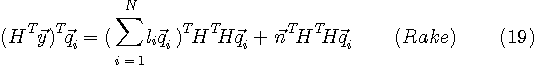|
最尤系列推定 Maximum likelihood sequence estimation |
|
ディジタル伝送の物理層の最終評価は誤り率で決まります。 物理的なシンボル値の判定は、大変基本的なことなので、正確に把握しておく必要があります。 ”シンボル”は、物理的な電圧に対応した値を指します。 たとえば、8値シンボル(3ビット)がパルス電圧値、 この信号を等間隔にサンプルして、 と考えてみます。 でも、実際の受信のプロセスは次のようなものです。 シンボルが次々と送信される このプロセスをイメージすると、 『サンプルごとに判定する』というのは、ちょっと単純過ぎる ことに気づきますね。 実は、 『系列として判定する』ことが常套的なのです。 では、そのような誤り確率を最小にする判定法をどうやって設計するのか? 腰を据えて、具体的に考えないとダメみたいですね。 上のプロセスで、『受信信号を適当な時間位相でサンプルした結果』が次のように表わせるとします。
ここで、送信シンボル系列
となり、『シンボルごとに判定する』が正解です。 しかし、実際には、チャンネル歪みによって、ナイキスト条件は満されないので、式(1)を前提に、『系列として判定すること』を考えなければなりません。 理解を容易にするため、先ず、『シンボルごとに判定する』場合(スカラーのケース)について説明します。この結果から、ベクトルのケースへ拡張は簡単です。 送信レベルを
になります。 また、正答率は、
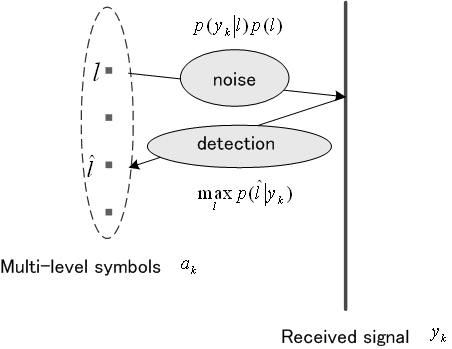
です。 いま、受信者は送信レベル 受信信号 といえます。 判定結果
を満たすレベルを選択することになります。
実際には、事後確率のテーブルを予め作っておきますが、それはベイズの公式から次の式で計算できます。
雑音がAWGNのときは、
で計算します。 注1:一般的に加法的”有色”ガウス雑音としたMAPの原理は最大事後確率判定法を参照。 もし送信レベルが等確率ならば、
だけで済みます。 これは、条件付確率の結果を固定し、原因を変数としてサーチしています。 このような関数を尤(ユウ)度関数 (liklihood function ) と呼んでいます。 そして、この判定法を最尤(ユウ)判定法 (Maximum Likelihood Detection: ML ) と呼んでいます。 さらに、式(8)の最大化は
と同じですから、テーブルを用意しないで、単に受信信号に一番近いレベルを、シンボルごとに判定すれば済むことになります。 注2: ほとんどのディジタル通信では、スクランブラーによってレベル値はランダム化され、等確率を前提にできます。 注3: 無線通信や金属線通信などの設計ではAWGNを前提としていますが、光ファイバー通信では、雑音は光の強度に応じて変化するのでAWGNは仮定できません。 上で述べたスカラーの判定を多次元へ拡張することは(式(1)へ拡張することは)簡単です。実際の通信では、非常に長いシンボルが送信されるとして、系列推定を実行します。その長さ
この場合、条件付確率は
と書けますが、上で述べたように、単に
によって系列
以上は、実シンボルを対象にしていますが、複素シンボル(QAM)への拡張は簡単なので省きます。 注4: チャンネル応答が未知の場合はブラインド系列推定の問題になり難しくなります。 このページを参照してください。 さて、M元伝送 (M-ary transmission ) のMLSEを当たってみましょう。 M元伝送は、互いに直交するN個の信号に送信データを掛けて重畳して送信する方法です。特に、直交信号が±1の符号系列のときCDMAと呼ばれています。
を作り、シンボル(上でいうレベル で表すと、送信信号(長さNの信号)は次のようになります。
ここで、
とすると、この場合のMLSEは前述と同じストーリーであり、
のように書けます。 この最小化を満たす
等化では、逆行列 最後に、OFDMのMLSEを当たってみます。 OFDMの原理は、送信シンボル列
これは式(12)とまったく同じです。 |
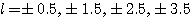 ボルトのどれかに対応するといったように。 この物理的なシンボルを
ボルトのどれかに対応するといったように。 この物理的なシンボルを
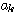 (
(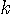 は時刻)で表すことにします。
は時刻)で表すことにします。 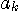 を次々と送信すると、いろいろな伝送障害を受けて受信されますが、まずは、
を次々と送信すると、いろいろな伝送障害を受けて受信されますが、まずは、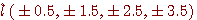 を判定する。
を判定する。 となる頻度がシンボル誤り率を与える。
となる頻度がシンボル誤り率を与える。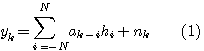
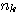 は加法的白色ガウス雑音 ( Additive White Gaussian Noise:: AWGN ) としておきます。 もし、
は加法的白色ガウス雑音 ( Additive White Gaussian Noise:: AWGN ) としておきます。 もし、
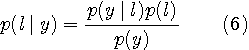
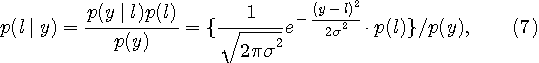
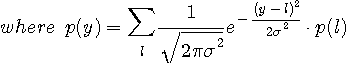
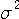 は雑音電力です。 実際には、受信信号
は雑音電力です。 実際には、受信信号 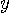 は固定されているので、式(6)あるいは(7)の分母
は固定されているので、式(6)あるいは(7)の分母 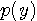 は不要です。 以上のような判定法を最大事後確率判定法 (Maximum
Aposteriory Probability detection : MAP ) と呼んでいます。
は不要です。 以上のような判定法を最大事後確率判定法 (Maximum
Aposteriory Probability detection : MAP ) と呼んでいます。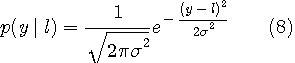
 、AWGN系列をベクトル
、AWGN系列をベクトル  で表すと、受信信号ベクトルは次のようになります。
で表すと、受信信号ベクトルは次のようになります。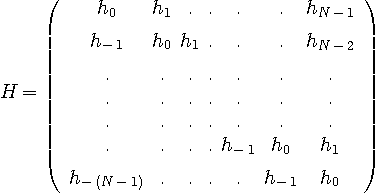
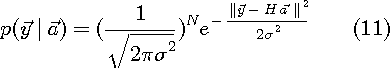
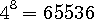 になります。 シンボル長が長くなるとたいまち計算量は爆発してしまいます。しかし、計算量をシンボル長に比例するようにできれば、いくらシンボル長が長くなっても平気です。これは
になります。 シンボル長が長くなるとたいまち計算量は爆発してしまいます。しかし、計算量をシンボル長に比例するようにできれば、いくらシンボル長が長くなっても平気です。これは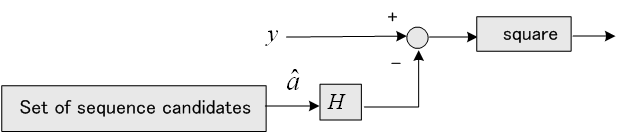
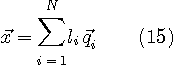
 が運ぶ情報は
が運ぶ情報は