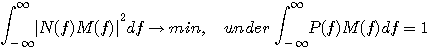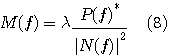|
整合フィルターがどのような局面で登場するかは後回しにして、先ず、一つの孤立パルスの極性に2値データ (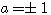 ) を乗せて送る場合を想定してください。受信パルスはチャンネルで歪を受け、受信端で雑音 ) を乗せて送る場合を想定してください。受信パルスはチャンネルで歪を受け、受信端で雑音 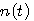 が重畳されるとします。 が重畳されるとします。
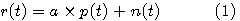
この受信信号から2値データ a を最も正確に判定するフィルターが整合フィルターです。この問題は以下ように変分法で解くことができます。
まず、周波数領域で以下の記号を定義します。
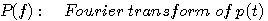
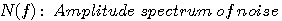
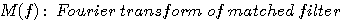
変分問題は、フィルター後において、パルスのピーク値を1 に拘束して雑音電力を最小にすることになります。
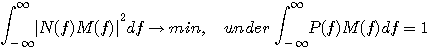
これを解いてみましょう。微小変分 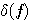 も係数 も係数 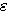 も複素数として、 も複素数として、
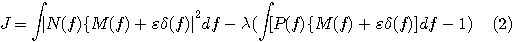
の 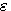 による偏微分が、 による偏微分が、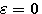 のとき、 のとき、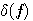 に関せずゼロになるような に関せずゼロになるような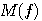 を求めればよいので、まず、 を求めればよいので、まず、
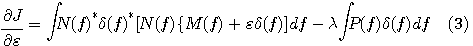
よって、Cauchy-Reimannの関係式を参照して、
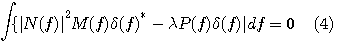
が得られ、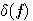 によらず上式が成立するためには によらず上式が成立するためには
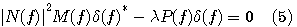
が必要です。両辺の複素共役をとると、
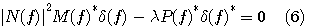
式(5)と式(6)を加えると、
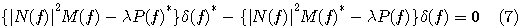
なので、整合フィルターが次のように得られます。
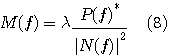
特に白色雑音ならば、単位周波数当たりの雑音電力を 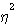 として、 として、
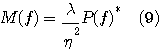
となります。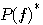 のフーリエ逆変換は のフーリエ逆変換は  なので、歪んだ受信パルスを時間反転したものが整合フィルターになります。あとは、ラグランジェの未定係数 なので、歪んだ受信パルスを時間反転したものが整合フィルターになります。あとは、ラグランジェの未定係数 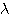 を適当に調整して、ピークが1 になるようにフィルターのゲインを調整します。 を適当に調整して、ピークが1 になるようにフィルターのゲインを調整します。
以下の数値シミュレーション(白色雑音を仮定)から視覚的にその効果を見ることができます。
- 図1=受信パルスの周波数特性
- 図2=受信パルスと雑音
- 図3=受信パルス+雑音
- 図4=整合フィルターの時間応答
- 図5=フィルター後のパルスと雑音
- 図6=フィルター後のパルス+雑音
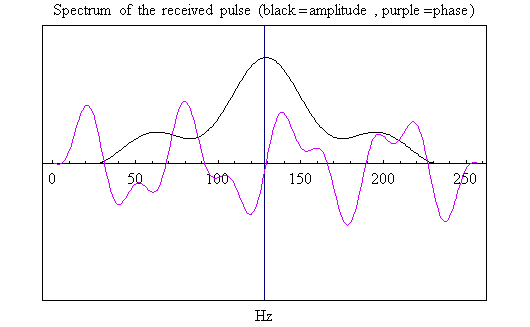
図1=受信パルスの周波数特性
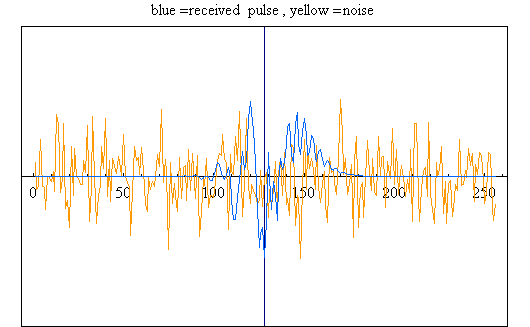
図2=受信パルスと雑音
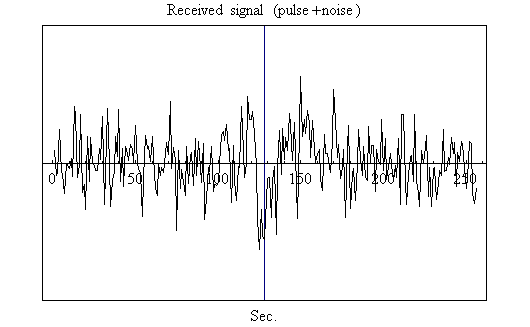
図3=受信パルス+雑音
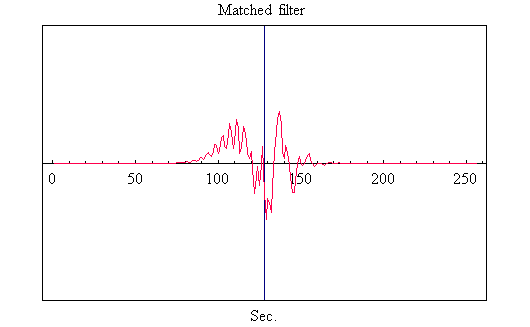
図4=整合フィルターの時間応答
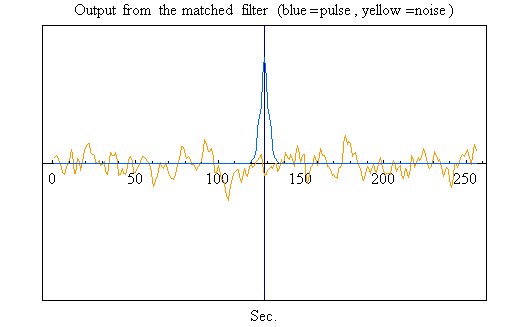
図5=フィルター後のパルスと雑音
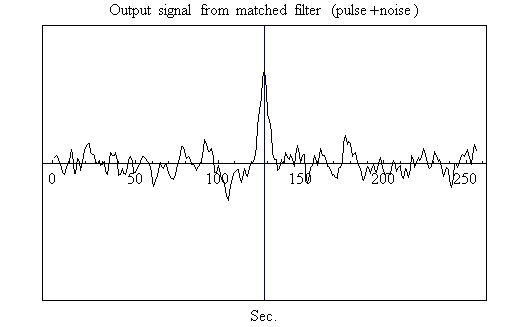
図6=フィルター後のパルス+雑音
さて、整合フィルターが登場する三つの局面を紹介します。
MLSE(Maximum Likelihood Sequence Detection:最尤系列推定) 予め定められた長さの送信データ系列(フレームと呼ぶ)がチャンネルを通過した信号を無雑音受信系列と呼ぶことにしましょう。この無雑音受信系列にAWGN(Additive White Gaussian Noise:加法的白色ガウス雑音)の系列が加算された場合、最小誤り率で送信データ系列を判定する方法が MLSEです。この判定は次のようです。まず、チャンネルのインパルス応答を推定する必要があり、これが整合フィルターとなります。すべてのフレームの無雑音受信系列を計算し、この中から最も受信系列(雑音あり)との距離(平均自乗誤差)が短い系列を選択します。この計算量はフレーム長の自乗に比例して大きくなります。これを、フレーム長に比例するように簡略化したものが ビタビ・アルゴリズムです。 整合フィルターの推定は、符号形式スペクトル拡散や CDM(符号分割多重)の場合は、受信系列(雑音あり)と既知PN系列との相互相関によって得られます( RAKEを参照)。 ブラインド系列推定 符号形式スペクトル拡散を採用しないで、データ系列を直接的に送る高速ストリーム伝送(非フレーム伝送)を前提にします。このとき、もし整合フィルターが推定されていれば、ビタビ・アルゴリズムを用いて逐次的に送信データを判定することができます。しかし、スペクトル拡散のようにPN系列に頼ることができないので、整合フィルターを推定する手段がありません。ここで、「送信データ系列も未知、チャンネル応答も未知」という原理的不可能に陥ってしまいます。一般に、これをブラインド問題と呼んでおり、付帯条件無しには解決できません。送信データが離散的(例えば2値とか4値とか・・・・)なケースならば、この問題を解決できます。ブラインド系列推定(ビタビ・アルゴリズムのブラインド版)の概略は ブラインド問題のページを参照してください。詳しくは、そのページからリンクされている解説論文(PDF)を開いてください。 ブラインド等化 上と同じく、符号形式スペクトル拡散をしないで、データ系列を直接的に送る高速ストリーム伝送を前提にします。高速通信モードでは、ブラインド等化を実施します。等化はチャンネル応答によって性能が左右され、MLSEに比べて、最適性が劣ります。しかし、ビタビ・アルゴリズムのような複雑な処理と異なり回路化が簡単なので広く実用されています。もし雑音が非常に大きく、等化しても通信できない場合は、パルス間隔を広げてパルス1個当たりの電力を大きくしてSNRを稼ぎます(送信電力の規格による)。このとき、ブラインド等化器は、雑音と符号間干渉の両者に対して最適な耐性を実現する解に収束します。パルス間隔を広げていくと、ブラインド等化器は自動的に整合フィルターに収束します。ブラインド等化の概略は ブラインド問題のページを参照してください。詳しくは、そのページからリンクされている解説論文(PDF)を開いてください。
|