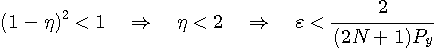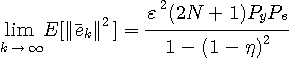|
確率的勾配法等化アルゴリズム Stochastic gradient equalization algorithm |
|
これは自乗平均誤差
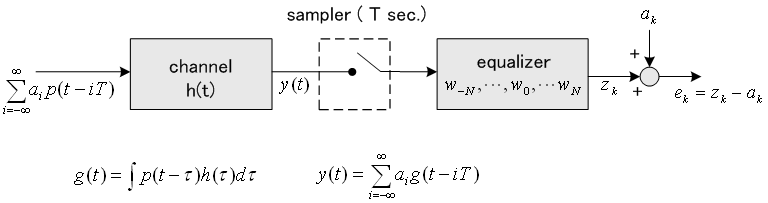
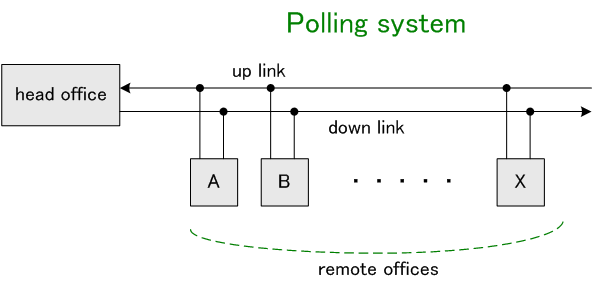
ここでは、シンボルレート等化について説明しますが、ダブルサンプリング等化も形式的には同じです。 ただし、ダブルサンプリング固有の収束の遅さの問題が発生するので、これらのことに関しては、高速収束等化で触れることにします。 昔のデータ通信の話になりますが、電話回線用アナログモデムの標準規格(CCITT.Vシリーズ)では、ポーリングシステムを前提にして、次のような規格が勧告されています。
上り回線では、ポーリングされた支店から順次データフレームが送られますが、各支店から本店への回線特性が異なるのでチャンネル歪も異なります。 したがって、本店では各支店ごとに上りの等化が必要になります。 この等化に要する時間がフレーム長に占める割合を小さくすることが重要になってきます。 規格では、データフレームの前に予め決められたランダムデータが送られ、この間に「強制等化(送信シンボルを既知とする等化)」を実行します。 これ以降は、緩慢な歪みの変動に追随するために、判例結果を正しいとし信じて等化器を継続的に調整します。 このモードを「適応等化」とか「仮判定等化」などと呼んでいます。 既知ランダムデータを「トレーニングシーケンス」と呼んでいますが、この同期は直前に送られる繰り返しデータの終わりを検出して知ることができるようになっています。 下り回線では、信号エネルギーを中断しないように、スクランブルされたデータが常に送られています。 各支店は、電源をONにすると、ブラインド等化でリンクを確立しなければなりません。 さて、自乗平均誤差 確率的勾配法等化アルゴリズムは、毎時刻において、
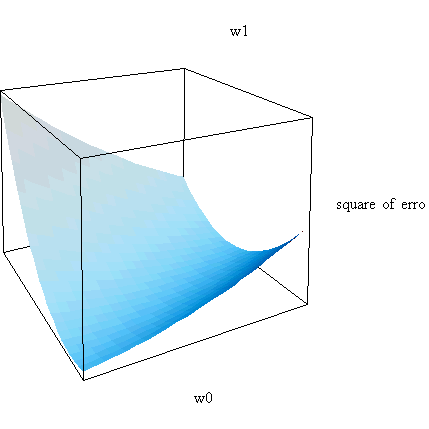
を繰り返します。 これは次のことを予想しています。 とりあえず、時刻 k の瞬時的自乗誤差を小さくするようにちょっとだけ修正し、 2タップの簡単なケースで、この予想を幾何学的に想像してみましょう。 時刻 k での自乗誤差
は、下図のように紙の両端をつまんで持ち上げた形をしています。 紙の底は直線
であり、そこでは最小値をとります。
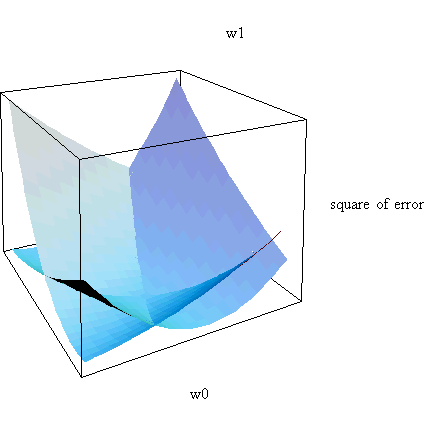
次の時刻の自乗誤差
も、下図のように紙の両端を持ち上げた曲面ですが、底の直線や勾配が異なります。
上の二つの図を重ねて描くと下のようになっています。
アルゴリズム(*)は、時々刻々、紙の曲面は切り替わるが、その紙に沿って下へ下へと(偏微分と逆の方向へと)、慎重に降りていこうという戦略です。 偏微分と逆方向へ降りることは、その曲面の直線の谷筋を目がけて降りることですが、谷筋がランダムに回転するので、右往左往しながら谷筋の”交点”へ向かうことになりそうです。 しかし、有限長等化器では等化誤差が正確にゼロになることはないので、
以下、タップ係数が期待値としてどのように収束するかを計算し、実際にシミュレーションで当たってみましょう。 式(*)は具体的に次のように書けます。
以下、次のようなベクトル表現を扱います。 ランダムな送信データ
ここで、
上の漸化式を、誤差ベクトル
ここで
のように分解できます。 したがって、
さらに、
とおいて、
のように、最終的にスカラー式に分解できました。 これら、2N+1個のスカラー式について、
が成り立っていれば期待値
以上は、期待値の収束でしたが、期待値のまわりでの分散が抑えられないと本当の収束が保証されません。 実際、
の両辺のノルムをとります。
ここで、もしタップ数が十分多いとすると、常に
となります。 この右辺を展開すると、
が得られますが、任意のベクトルについて成り立つシュワルツの公式、
から、修正係数を
に選んでおけば、式(***)はいつも
のように書け、単調にゼロに収束することがいえます。 以上はタップ数が無限に多いときでしたが、これを有限とした場合について検討しておきます。 この場合は、式(**)の期待値をとってみます。
右辺第2項は、誤差ベクトル
ただし、
に選べば、単調減少がいえます。 等化後の誤差は近似的に、
で与えられます。 |
 を修正することになります。 この修正はオンライン的に実行されるのですが、目標
となる平均自乗誤差
を修正することになります。 この修正はオンライン的に実行されるのですが、目標
となる平均自乗誤差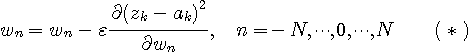

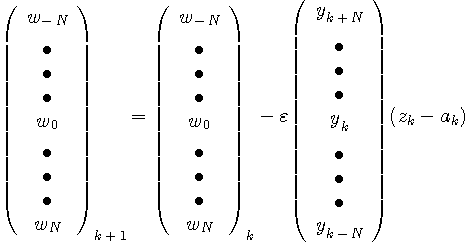
 は必ずあります。 もし、負の固有値があると、
は必ずあります。 もし、負の固有値があると、  を小さくする必要があります。 このとき最小固有値に対しては
を小さくする必要があります。 このとき最小固有値に対しては 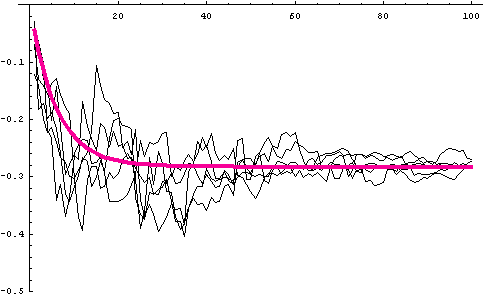
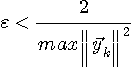
 は
は