

|
帯域制限パルス Bandlimited pulse |
|
無線通信において周波数は公共の財産です。 どんな通信も、使用できる周波数帯域が許可されて始めて実用できます。 許可された周波数帯域の中に信号エネルギーを押し込める技術が変調です。 送りたい信号をベースバンド(基底帯域)信号といいますが、振幅変調 (AM:: Amplitude Modulation ) は、ベースバンド信号の周波数成分(スペクトルと呼ぶ)を許可された高い周波数帯域へそのまま平行移動します。 したがって、ベースバンド信号の帯域幅が許可されたチャンネルの帯域幅に制限されていなければなりません。 周波数変調 (FM:: Frequency Modulation ) では厳密な意味で帯域制限を実現できませんが、規格は帯域外への漏洩電力の上限で与えられるので、実用は可能です。周波数変調を参照してください。 パルスの話をするのに、いきなり変調の話をしてしまいましたが、変調という概念を理解しないと通信で用いるパルスが理解できません。 そういうわけで、まずは変調の仕組みを簡単に分かってください。 一言で振幅変調といってもいろいろ種類がありますが、通常は両側帯波振幅変調(BSBAM: Both/Double Side Band Amplitude Modulation ) のことを指します。 ではまず、送信ベースバンドパルスのスペクトルが、BSBAMによって許可された高周波帯域に移動することをたしかめてみましょう。 パルスを
を満たしているとします。 これを仮定する理由は、下のフーリエ変換が有限な値で決まるためです。 すなわち、無限の大きさをもつスペクトルを排除したわけです。 物理的には、そんなことはあり得ないのですが、念のためということです。
左辺の
このスペクトルがどうなるか見てみましょう。 そのために、上式をフーリエ変換してみます。
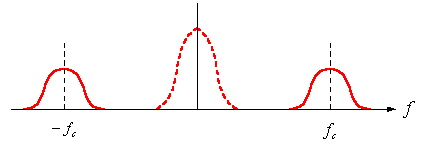
上の式は、下図のようにスペクトルの平行移動を表しています。 すなわち、ベースバンド信号のスペクトルが半分づつに分かれて正の搬送波周波数 と負の搬送波周波数 のところへ平行移動しました。 したがって、ベースバンドパルス (下図の赤い点線)が許可された幅に帯域制限されていればいいわけです。 なお、周波数に正と負があることは奇異に感じると思いますが、本当はこのように考えないと変調は理解できません。 図1
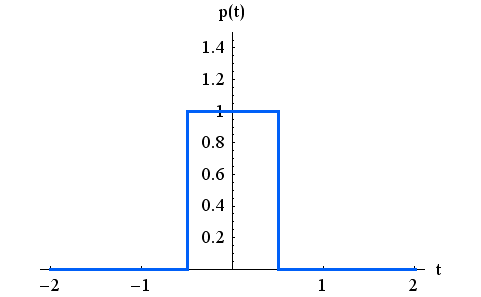
それでは、スペクトル幅が制限されたパルスはどんな形をしているでしょうか? 普通、パルスといえば、図2のような矩形パルスを想像しますね。 パソコンの中を駆け巡っているパルスはきっとこれでしょう。 図2で横軸は秒、縦軸 はパルス電圧と見てください。
では、このパルスのスペクトルを計算してみましょう。 そのためにフーリェ変換してみると、結果は次のようになります。
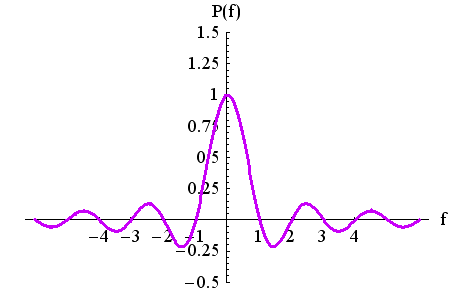
図3
この形から分かるように、矩形パルスは無限に高い周波数成分をもっています。 したがって、帯域が厳密に制限される通信では、こんなパルスを用いることはできません。 このことは、みなさんが使っているケイタイやADSLなど、すべてのパルス通信についていえることです。 では、通信では 上のストーリーでは、パルスとスペクトルは実数値でした。 この実関数で話を進めます。フーリェ変換の逆変換は定数倍を無視すると次のように書けます。
前記したフーリェ変換とずいぶん似ていますね。 違いは、 LSIエンジニアは、演算速度を上げるため、 それでは、グラフの横軸をちゃんと交換して、描きなおしておきましょう。 ついでに、ちょっと現実的に、チャンネル幅を10kHzとした場合の単位を振っておきます。
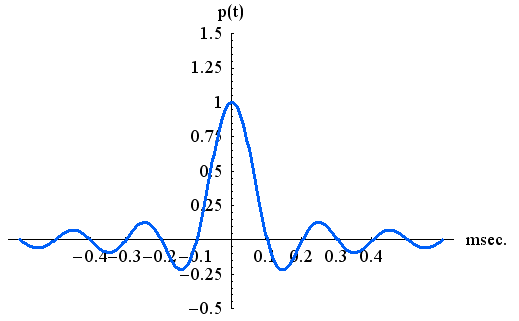
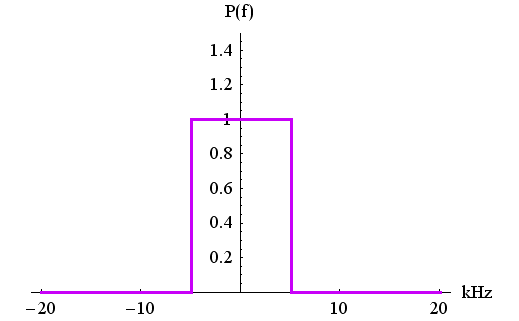
上の青色のパルスは標本化関数(sampling function)と呼ばれ、いろんな場面で登場します。 帯域幅
実際には、正確な矩形スペクトルをもつパルスを回路的に実現することができません。 そこで、矩形スペクトルの肩をなだらかにしたようなパルスを用います。 ナデ肩にすることをロールオフ(roll off )するといっています。 広く用いられるロールオフは余弦曲線によるもので、次のようです。 Wの単位は Hz です。
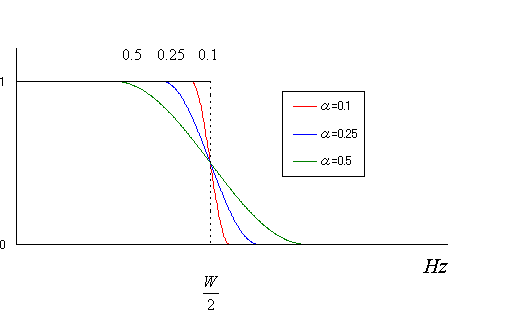
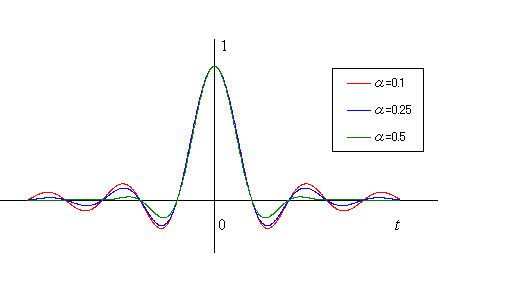
ロールオフ率
は、下図のように裾が速く減衰するようになります。 ただし、完全にゼロになるわけではありません。
このパルスをよく見ると、ピークを除いてちょうど 注: 帯域制限されたパルス |
 は時間を表し、
は時間を表し、 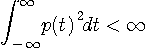
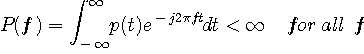
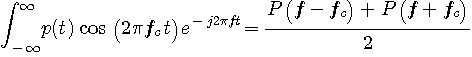
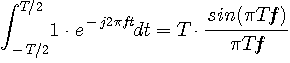
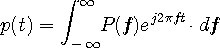
 を大きくすれば、パルス
を大きくすれば、パルス 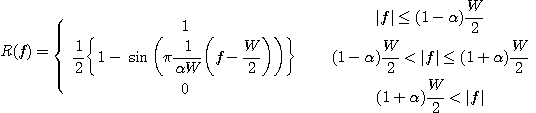
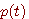 は時間制限されません。言い換えれば、パルスとそのスペクトルが同時に有限区間内に収まることはないということです。なお、両者のエネルギーを出来るだけ有限区間内に集中させる問題は
は時間制限されません。言い換えれば、パルスとそのスペクトルが同時に有限区間内に収まることはないということです。なお、両者のエネルギーを出来るだけ有限区間内に集中させる問題は