|
周波数 Frequency |
|
１ｋ（Hｚ）という周波数は、１秒間に１０００回単振動を繰り返すとことを意味します。 単振動とは、紐にぶら下げられた錘が行ったり来たりする振り子運動のようなものです。 振幅が微小ならば平衡点からの距離は、正弦関数
で与えられます。
のように表現してみましょう。 ところが、周波数の正と負は上のような表現では区別できないことが分かります。 たとえば、初期位相が
のような関係にあれば、常に
となり、周波数の正負は関係なくなってしまいます。 そこで、もっと基本的な表現法を導入します。 それは複素信号
による表現です。 この実部は余弦関数、虚部は正弦関数です。 複素信号
このように、複素信号を使えば、周波数の正負を区別して表現することができます。 周波数の符号を意識することは、通信工学においては極めて重要なことです。 特に変調では、周波数の符号が重要な意味をもちます。 周波数という概念は永遠に等速円運動するということを意味します。 紐のまわりを回転する錘が床や空気から抵抗を受けなければ、錘は永遠に等速で回り続けるわけです。 この意味からすれば、「現在の周波数は １ｋ Hz です」という言い方は矛盾しています。 現在が １ｋ Hz ならば過去も未来もぴったり １ｋ Hz でなければなりません。 このように、 周波数は 「永遠」 という抽象的な概念を含んでいる ことに注意してください。 １ｋ Hｚ の振動が続いているようでも、その振幅
となり、周波数
この周波数差
周波数成分の分析精度を上げようとすると、 ということがいえます。 しかし、現実には、たとえ周期信号であることが分かっている場合でも、周期や周波数成分の個数などの予備知識がないのが普通です。 さらに言えば、僕たちが見たり聞いたりする信号や、電波で発信される信号など、ほとんどは非周期信号です。 われわれの耳では、音波によって鼓膜の振動がリンパ液で満たされた蝸牛（カタツムリ）管を伝播し、蝸牛管を縦に仕切るように張られた膜が共振します。 膜には長軸と直角に無数の繊維が通っており、膜の振動を受容します。 長軸方向に膜の共振周波数が変わるようになっており、膜のどこが共振するかというパターンが音に含まれる短時間周波数成分のパターンに一致し、それを知覚して音楽を聴いたり、話を聞いたりしています。 短時間周波数成分のパターンは時間的に変化し、この変化が情報を伝えます。 したがって、短時間周波数成分の強さが時間的に変化するものとして、信号を分析する新しい手法をもちこまなければ通信や画像処理や生理学など、すべての分野で有効な議論ができません。 このような観点から信号をどのように分解したらいいか、いろんな研究がなされています。 たとえば、周波数分析やWaveletやパルスの不確定性を参照してください。 聴覚に関する解剖学的な内容に関しては下のサイトを参照してください。 |
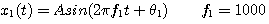
は最大振幅、
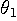は時刻ゼロでの初期位相です。 通常、われわれは周波数に符号を意識しませんが、負の１ｋ（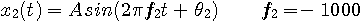
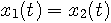
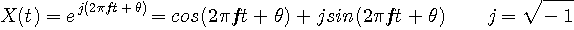
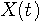は複素平面上の単位円の上を一定の速度で回転します。 もし周波数が正ならば反時計回りに、負ならば時計回りに回転します。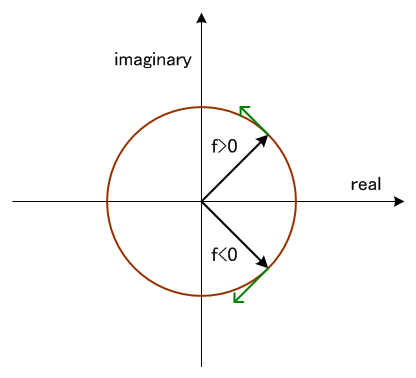
がゆっくり変化していると、純粋な １ｋ Hz かどうか疑わしくなります。 たとえば、周波数がわずかに違う二つの振動音を同時に聞くと、ぼくたちはウナリを聞きます。 二つの周波数差を
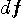とすると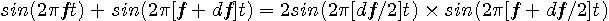
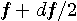Hzの音が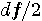 
Hz のゆっくりした周波数で強弱を繰り返すように聞こえます。 実は、周波数
Hzの音と周波数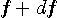 
Hzの音が加算されたものだとはあまり意識しません。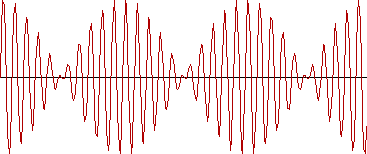
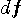が非常に小さいと、１周期のウナリを聞き終わるまでに長い時間がかかります。 上の図は、ウナリの２周期分を描いたものです。 もし、予め周波数差が分かっていると仮定します。 すると、ちょうど周波数差の時間を切り出し、これを