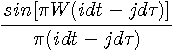|
時間・周波数の2次元空間の上で、信号を分析したり合成したりすることは、信号の細部の振る舞いを視覚的に表すことができ、非常に有効な手段です。高速通信でのパルス設計や周波数分析の窓関数設計において、パルス(あるいわ窓関数)は時間幅を狭めようとすると周波数幅が広がり、時間軸と周波数軸で反比例の関係があります。パルスの時間的広がりを T とし、その周波数スペクトルの広がりを F としたとき、T+F あるいは T×F などが最小になるような極小パルスを追求する問題が古くから追及されてきました。この問題を最初に扱った人はギャボア(Dennis Gabor, 1900-1979、ホログラフィーの発明でノーベル物理学賞を受けている)ではないかと思います。彼は、後述のガウスパルスを時間軸と周波数軸にシフトして、それらの重畳によって、どんな信号も合成できるとしました。しかし、ガウスパルスはシフトした周辺のパルスと直交していないので、どんな信号も合成できる(完備性)と言うのは疑問です。 工学的な立場に立てば、必ずしも極小パルスを狙う必要はなく、むしろ、時間・周波数平面で互いに直交するようなパルスによって完備性を確保することの方が重要です。そんな理由から、信号の完全表現に関心が集まり、ウェーブレットが生まれました。
簡単のため、このページで扱うパルス 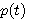 は、すべて実数とします。 また、時間原点 は、すべて実数とします。 また、時間原点  に対して非対称なパルスは意味がないので、初めから対称パルスを前提とします。 定数倍も含めて、正確なフーリエ変換とその逆変換を次のように定義しておきます。 に対して非対称なパルスは意味がないので、初めから対称パルスを前提とします。 定数倍も含めて、正確なフーリエ変換とその逆変換を次のように定義しておきます。
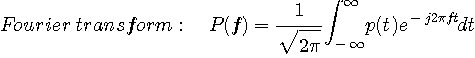
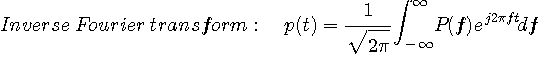
パルス 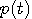 を実数かつ対称としているので、フーリエ変換と逆変換はまったく同じものになります。 パルスのエネルギーを を実数かつ対称としているので、フーリエ変換と逆変換はまったく同じものになります。 パルスのエネルギーを
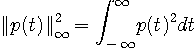
で表します。 パーセバル (Parseval) の定理から、
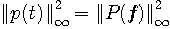
が成り立っています。
エネルギーを一定に保ったまま、パルスを引き伸ばしたり縮めたりすると、そのフーリエ変換は反比例して縮まったり伸びたりします。その様子をウェーブレットで登場したメキシカンハットで見ると下図のようです。上が引き伸ばした場合、下が縮めた場合です。

 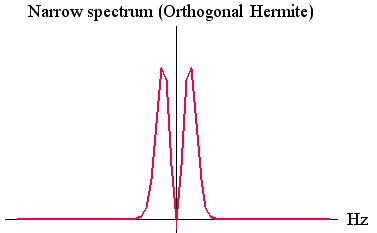
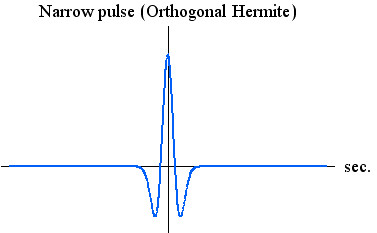 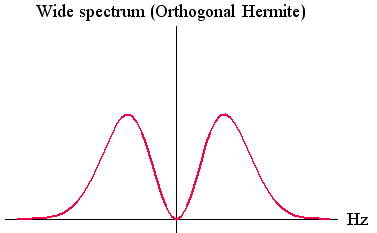
周波数分析で説明したように、窓関数(パルス)の時間幅を縮めると、時間の変化を細かく観測できるが、周波数の変化を正確に観測できなくなります。 逆に、時間幅を広げると周波数の観測精度は上がるが、時間変化の観測精度が落ちます。 両方の観測精度を同時にいくらでも上げるという虫のいい話はないけれど、精一杯努力して、その限界を与える窓関数はどんな形をしているかを求めることは大変興味深いことです。 そのためにはまず、時間幅とそのスペクトルの周波数幅を具体的に定義しなければなりません。 両方の定義は、必ずしも同じ意味である必要はなく、違った意味でもかまいませんが、目的に沿って決められるべきものです。 一般に、定義の物理的意味が異質だと、最適化問題を解くことが困難になってきます。 仮に
それらを  と と 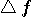 で表すと、エネルギーを一定に拘束して、 で表すと、エネルギーを一定に拘束して、
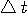 と と 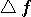 が同質の定義をもつ。 => 例:Gaussian Pulse が同質の定義をもつ。 => 例:Gaussian Pulse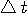 と と 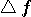 は異質な定義だが、一方を固定して他方の最小化が簡単。 は異質な定義だが、一方を固定して他方の最小化が簡単。
=> 例:Raised cosine pulse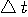 と と 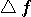 に、それぞれ二つの定義が与えられる。 これら4つを連動させて最小化を図る。 =>
例: Prolate spheroidal wave function に、それぞれ二つの定義が与えられる。 これら4つを連動させて最小化を図る。 =>
例: Prolate spheroidal wave function
といったような問題を解くことになります。 以下、上の典型的な3つの例について説明します。
1.Gaussian pulse
パルスとそのスペクトルの幅をエネルギーの2次モーメント
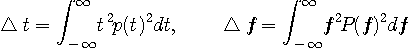
で定義し、それらの積をエネルギー一定のもとで最小化します。
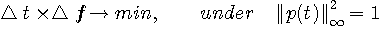
変分問題を時間領域で処理するために、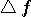 を次のように時間軸へ変換します。 を次のように時間軸へ変換します。 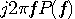 は時間領域で、 は時間領域で、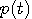 を微分することでした。 したがって、 を微分することでした。 したがって、
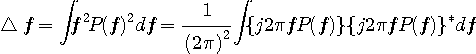
右肩の*印は複素共役で、さらに、パーセバルの定理から次が得られます。
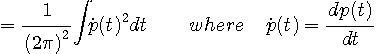
変分問題は、任意の摂動 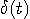 について、汎関数 (functional ) について、汎関数 (functional )
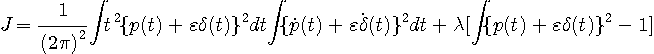
が  に関して極値となる関数を求めることです。 に関して極値となる関数を求めることです。
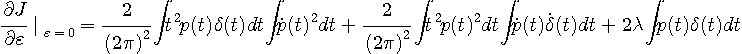
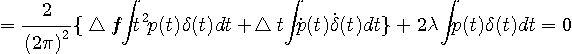
ここで、
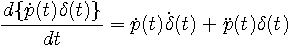
を代入して、
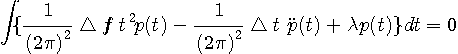
なので、次の微分方程式の自明でない解を求める問題に帰着しました。
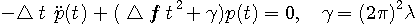
求める解は、未定乗数が  のとき、 のとき、
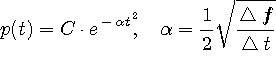
のようになり、さらに、拘束条件 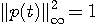 を満たすように を満たすように  を決めると次が得られます。 を決めると次が得られます。

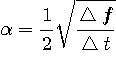
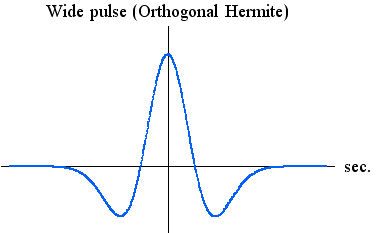
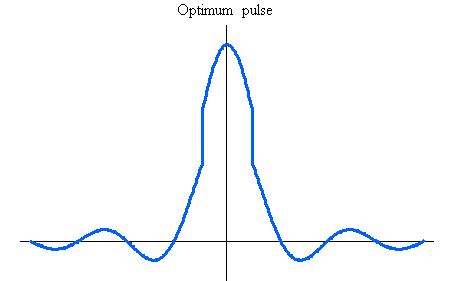
パルスとそのスペクトルは同じ関数であり、下図のようです。
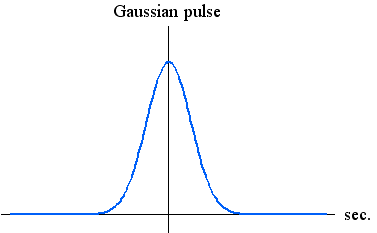 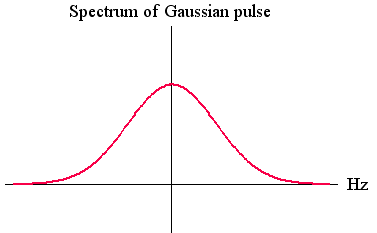
2. Raised cosine pulse
パルスを帯域制限し、エネルギー一定の条件のもとで、エネルギーの2次モーメントを最小にします。
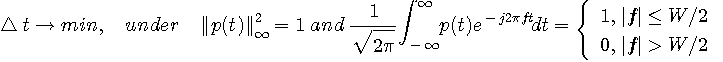
結果は、100%ロールオフナイキストパルス(スペクトルが Raised
cosine )になります。 一応、変分法で解いてみましょう。 ストレートに汎関数を書くと次のようです。 特に示さない限り、積分領域は
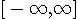 とします。 とします。
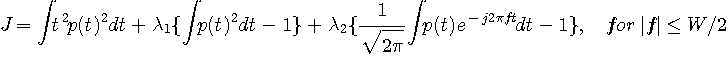
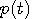 に任意の摂動を与えると、 に任意の摂動を与えると、
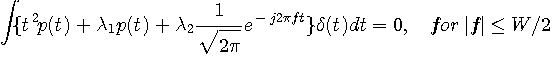
が得られ、{ }内が 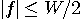 に対して恒等的にゼロになるような に対して恒等的にゼロになるような 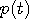 が求めるパルスです。 { }内をフーリエ変換します。 が求めるパルスです。 { }内をフーリエ変換します。 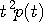 のフーリエ変換は のフーリエ変換は 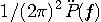 であり、 であり、 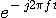 のフーリエ変換はデルタ関数になるので、結果は次のようになります。 のフーリエ変換はデルタ関数になるので、結果は次のようになります。
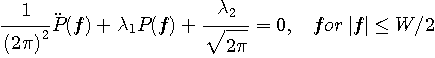
未定乗数などを簡単化して、
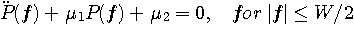
この問題の性質から、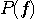 は実数値かつ対称としていいので、その範囲で上式を満たす は実数値かつ対称としていいので、その範囲で上式を満たす 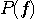 は帯域 [-W/2, W/2] に制限された は帯域 [-W/2, W/2] に制限された
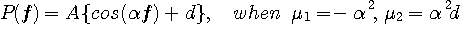
のような raised cosine に限定されます。 この形式が極値を与えますが、まだ
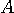 と と  と と  を決めなければなりません。 そのためには、2次モーメント を決めなければなりません。 そのためには、2次モーメント 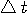 を最小にする値のセットを求めればいいのですが、計算過程がかなり退屈なので直感的にいきましょう。 まず を最小にする値のセットを求めればいいのですが、計算過程がかなり退屈なので直感的にいきましょう。 まず 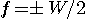 で不連続点をもつようなスペクトルのパルスはなかなか減衰しない裾をもつので除きます。 すると、 で不連続点をもつようなスペクトルのパルスはなかなか減衰しない裾をもつので除きます。 すると、
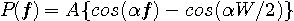
となります。 さらに、一回微分が 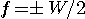 で不連続となるケースもパルスの裾を長くするので除きます。 すると、 で不連続となるケースもパルスの裾を長くするので除きます。 すると、
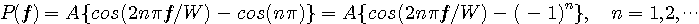
が得られます。 後は、 を決めれば済みますが、計算するまでもなく を決めれば済みますが、計算するまでもなく 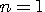 が答えです。 以上から、最適な解が次のように得られました。 が答えです。 以上から、最適な解が次のように得られました。

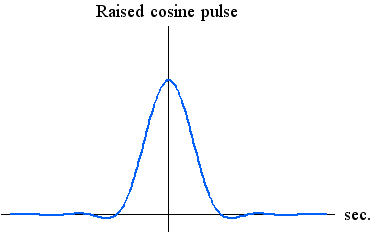 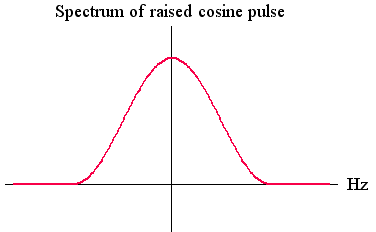
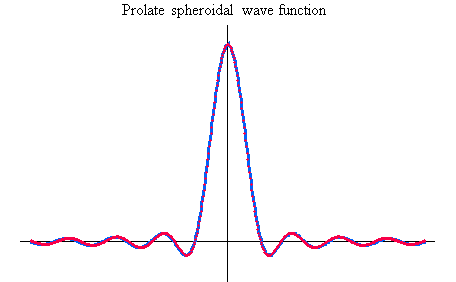
3. Prolate spheroidal wave function
パルスが区間
[-T/2,T/2] sec. に含まれるエネルギーを 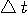 、そのスペクトルが区間 [-W/2,W/2] Hz に含まれるエネルギーを 、そのスペクトルが区間 [-W/2,W/2] Hz に含まれるエネルギーを 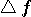 としたとき、パルスの全エネルギーが一定のもとで、 としたとき、パルスの全エネルギーが一定のもとで、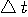 と と 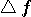 をともに大きくしようとする問題を扱います。 逆に言えば、 をともに大きくしようとする問題を扱います。 逆に言えば、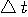 と と 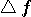 が与えられたとき、T と W をともに小さくする問題ということになります。 が与えられたとき、T と W をともに小さくする問題ということになります。
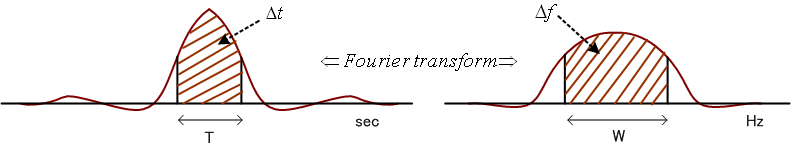
このような問題は、T, W, 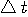 , , 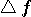 の4つが関連するので、ちょっと複雑になりそうです。 この問題は、1961年の4つのパートにわたる論文によって解かれました。 下に、重要な最初の二つの論文を記します。 かなり難解ですので、ここでは、そのストーリーを簡単に紹介します。 の4つが関連するので、ちょっと複雑になりそうです。 この問題は、1961年の4つのパートにわたる論文によって解かれました。 下に、重要な最初の二つの論文を記します。 かなり難解ですので、ここでは、そのストーリーを簡単に紹介します。
- D. Slepian and H.O.Pollak "Prolate Spheroidal Wave
Function, Fourier Analysis and Uncertaintry - Part1"
The Bell System Technical Journal, pp43-63, January 1961
- H.J.Landau and H.O.Pollak "Prolate Spheroidal Wave
Function, Fourier Analysis and Uncertaintry - Part2"
The Bell System Technical Journal, pp65-84, January 1961
まず、記号のルールを次のように定義します。
たとえば、具体的に書くと、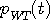 は、 は、
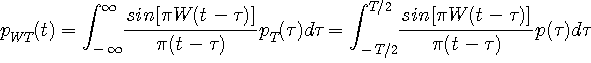
のような変換を表しています。 このように帯域制限されたパルス
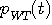 は無限に裾を引きます。 は無限に裾を引きます。 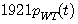 のエネルギーが大きいということは、時間制限されたパルス のエネルギーが大きいということは、時間制限されたパルス 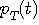 を理想低域通過炉波器( 帯域 [-W/2,W/2] 内の成分をそのまま通し、帯域外の成分をカットする)に通したとき、エネルギーをあまり失わないことを意味しています。 では、どんなパルス(時間制限に注意!)がもっともエネルギーを失わないでしょうか? その結論は次のようです。 を理想低域通過炉波器( 帯域 [-W/2,W/2] 内の成分をそのまま通し、帯域外の成分をカットする)に通したとき、エネルギーをあまり失わないことを意味しています。 では、どんなパルス(時間制限に注意!)がもっともエネルギーを失わないでしょうか? その結論は次のようです。
下記の式を満たす固有値  と正規直交固有関数 と正規直交固有関数  のペアは無限にあります。 のペアは無限にあります。
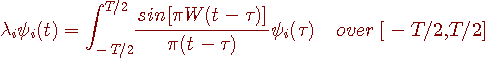
この中の最大固有値  の固有関数 の固有関数  が次の最大を与えます。 が次の最大を与えます。
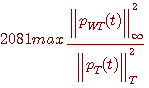
これは、変分法から容易に得られます。 汎関数
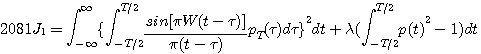
からスタートして、まず、
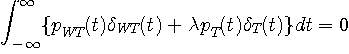
が得られますが、ここで、
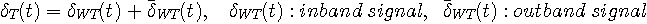
とおくと、
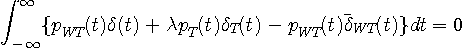
となり、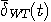 と と 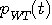 は互いに周波数帯域を共有していないので(直交しているので)、 は互いに周波数帯域を共有していないので(直交しているので)、
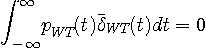
となり、解は
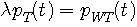
を満たすことが分かりました。 そして、固有値 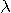 は は 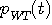 のエネルギーを与えているので、最大固有値を選択するのが正解です。 次に、時間制限された のエネルギーを与えているので、最大固有値を選択するのが正解です。 次に、時間制限された
 を区間 [-T/2,T/2] の外に外挿します。 この操作は、もう一度 を区間 [-T/2,T/2] の外に外挿します。 この操作は、もう一度  を低域通過炉波器に通せば得られます。 もちろん、区間 [-T/2,T/2] 内では上で求めた を低域通過炉波器に通せば得られます。 もちろん、区間 [-T/2,T/2] 内では上で求めた
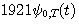 に一致しているはずです。 このようにして得られたパルスを同じ記号 に一致しているはずです。 このようにして得られたパルスを同じ記号 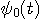 で表し、これを prolate spheroidal wave function と呼んでいます。 次のことが言えます。 で表し、これを prolate spheroidal wave function と呼んでいます。 次のことが言えます。
外挿された 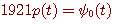 は次の最大を与える。 は次の最大を与える。
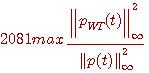
前記汎関数 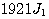 の右辺最後の積分範囲をちょっと変更して、次のように定義します。 の右辺最後の積分範囲をちょっと変更して、次のように定義します。
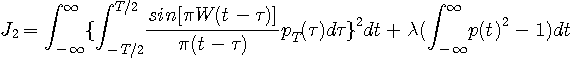
これに、上と同じような計算を実行して、
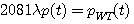
が得られます。 左辺の 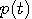 は時間制限されないパルスです。 以上までをまとめると、次のように言うことができます。 は時間制限されないパルスです。 以上までをまとめると、次のように言うことができます。
パルス 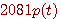 から区間 [-T/2,T/2]の部分を切り取る。 から区間 [-T/2,T/2]の部分を切り取る。
切り取られたパルスのスペクトルは無限に広がっている。
このスペクトルから区間
[-W/2,W/2] の部分を切り取る。
切り取られたスペクトルのフーリエ逆変換
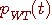 は、エネルギーを失っている。 は、エネルギーを失っている。
このエネルギー損失を最小にしたとき、
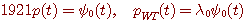
となり、  はエネルギーの最大減衰率を表し、積 はエネルギーの最大減衰率を表し、積  に依存する。 に依存する。
ここで、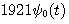 はどんな波形をしているか、数値計算で当たってみましょう。 適当な時間きざみでサンプルした はどんな波形をしているか、数値計算で当たってみましょう。 適当な時間きざみでサンプルした
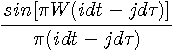
を 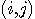 要素とする正方行列(奇数次元)を作り、固有値と固有ベクトルを求めるだけで済みます。 この正方行列は対称なので固有値は実数です。 最大固有値に対応した固有ベクトルで外挿した 要素とする正方行列(奇数次元)を作り、固有値と固有ベクトルを求めるだけで済みます。 この正方行列は対称なので固有値は実数です。 最大固有値に対応した固有ベクトルで外挿した
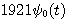 の波形は下図のようになります。 上から、 の波形は下図のようになります。 上から、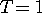 とし、 とし、 について示してあります。 青色が外挿された波形で、黒色は時間制限された部分を表しています。 について示してあります。 青色が外挿された波形で、黒色は時間制限された部分を表しています。
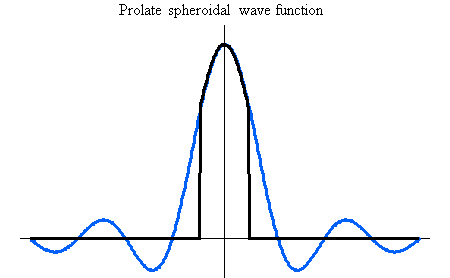
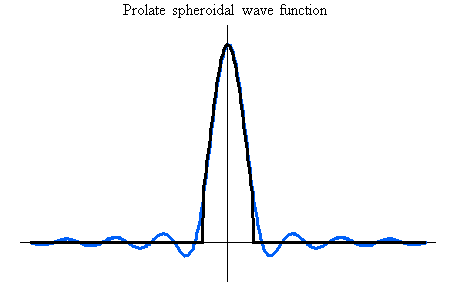
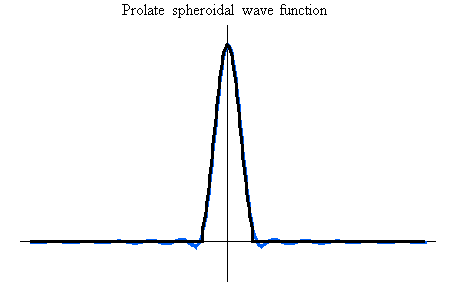
最後に、以上のすべての議論を周波数領域で書き換えるとまったく同様の道筋をたどり、その道筋は一意的なので、次が明らかです。 ただし、時間制限を帯域制限、帯域制限を時間制限と読み替えます。
時間制限された 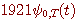 のフーリエ変換は、帯域制限なしの のフーリエ変換は、帯域制限なしの 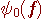 になる。 になる。
ただし、時間幅と帯域幅の比に応じて伸張・縮尺される。

上の図の青色の波形に、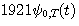 をフーリエ変換した赤色のドットを重ねてみると、たしかにピッタリ一致します。 下は、 をフーリエ変換した赤色のドットを重ねてみると、たしかにピッタリ一致します。 下は、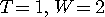 の場合について、重ねて描いたものです。 の場合について、重ねて描いたものです。
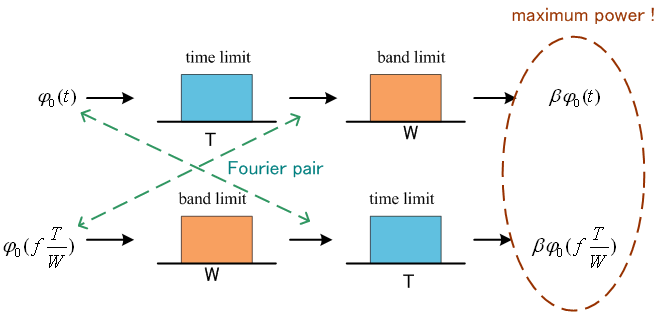
以上を整理すると、次のような絵が描けます。
ここまでの結果を上手く使って本題を解くわけですが、結果だけを要約します。 あとは、上記論文の
Part 2 を読んでください。
 が与えられると、 が与えられると、 が決まる。 が決まる。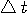 (区間 [-T/2,T/2] 内のエネルギー)が (区間 [-T/2,T/2] 内のエネルギー)が 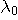 以下のとき、 以下のとき、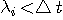 を満たす(固有値はゼロに収束する級数なので必ずある)任意の固有関数 を満たす(固有値はゼロに収束する級数なので必ずある)任意の固有関数 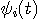 を一つ選んで、 を一つ選んで、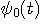 と と 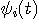 の一次結合で、 の一次結合で、 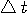 を実現するパルスを作ることができる。 そして、これはもともと帯域制限されたパルスなので、 を実現するパルスを作ることができる。 そして、これはもともと帯域制限されたパルスなので、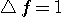 である。 同じことが、 である。 同じことが、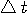 と と 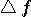 を入れ替えれていえる。 を入れ替えれていえる。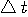 が が 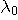 を越えたとき、 を越えたとき、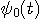 の区間 [-T/2,T/2] の部分をかさ上げして の区間 [-T/2,T/2] の部分をかさ上げして 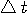 を実現する。 式で書けば、 を実現する。 式で書けば、 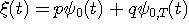 において、 において、  と と 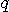 を を 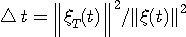 となるように決めることになる。 このとき、 となるように決めることになる。 このとき、 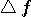 は一意に決まる。 その関係式は次のようである。 は一意に決まる。 その関係式は次のようである。
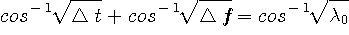
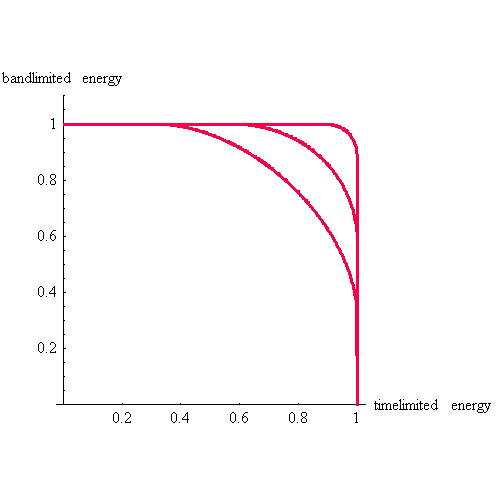
この不確定性を図示すると次のようになります。 横軸が
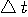 、縦軸が 、縦軸が 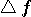 です。 です。 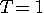 とし、下から、 とし、下から、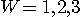 の順です。 の順です。
また、このときのパルスは、たとえば下図のように不連続点をもちます。 これをフーリエ変換すると、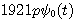 が帯域制限された が帯域制限された 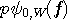 に、 に、 が帯域全域に広がる が帯域全域に広がる 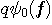 になり、 になり、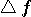 が自動的に決まります。 が自動的に決まります。
注1: ここでは孤立パルスを扱っていますが、実際の連続信号をどのようなパルス列で表現するのがよいかという問題が残ります。 Gaussian
pulse を用いて信号を時間・周波数空間で表現する問題が
D.Gabor (1900-1979) によって扱われたのは
1950年のことです。 このような研究を経て、ウェーブレットが発想されました。
注2: 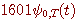 は次の微分方程式の区間 [-1,1] の解になります。 Prolate spheroidal wave
function はこの微分方程式から由来するものです。 は次の微分方程式の区間 [-1,1] の解になります。 Prolate spheroidal wave
function はこの微分方程式から由来するものです。  の離散値でのみ解をもちます。 の離散値でのみ解をもちます。

|


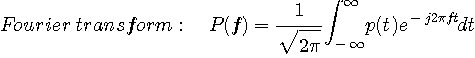
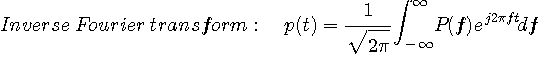
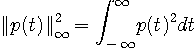





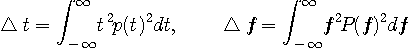
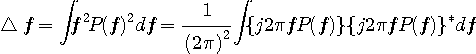
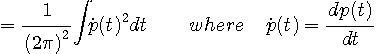
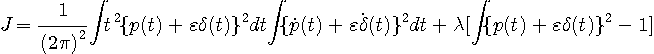
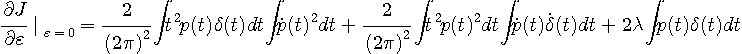
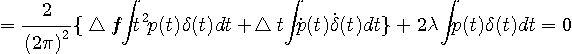
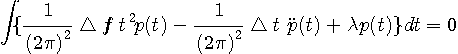
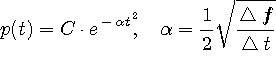

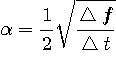


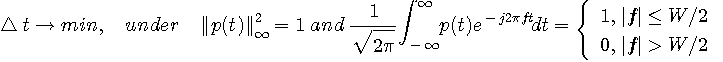
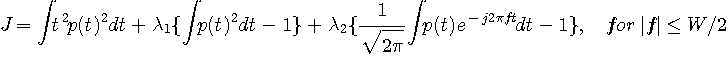
 に任意の摂動を与えると、
に任意の摂動を与えると、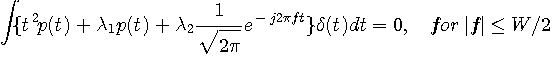
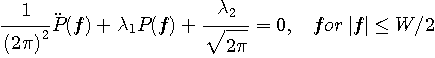



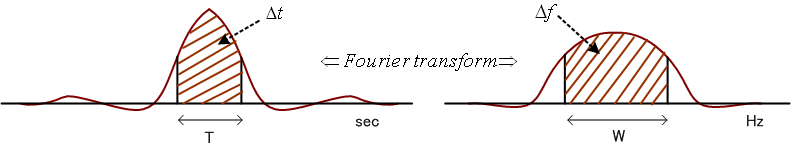
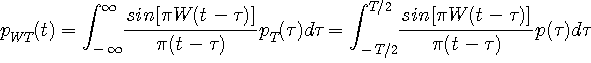
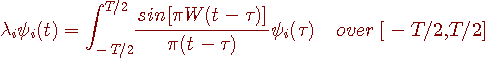
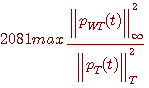
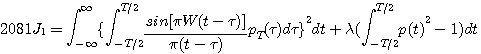
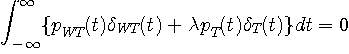
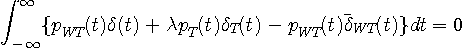
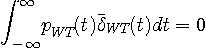
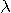 は
は 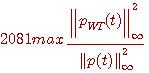
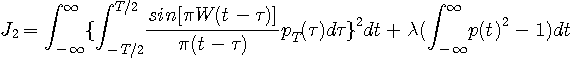
 に依存する。
に依存する。