|
フーリエ級数 Fourier series |
|
まず、信号を複数の直交信号に分解することの工学的意味を理解しましょう。 時刻 ０ から時刻 Ｔ までの信号を頭におき、この区間に、無限個の信号があり、それらを
と表します。 そして、これらは、下のように正規直交しているとします。
ここで、一次結合
で表現可能な信号の集合を想定します。 すると、この集合の任意の信号について、
が
が
どんな直交信号系が工学的に有用か？ に絞られます。 この条件を満たす代表的な直交展開がフーリエ
(Jean
Baptiste Joseph Fourier, 1768-1830)
級数です。 フーリェ級数は、対象とする信号波形に含まれる周波数成分を分析する目的で考え出されたものです。
を考えます。 これらはすべて、周期
のように直交条件が成り立っています。 自分自身の内積は非負の値をもち、
となります。 すべてについて自分自身の内積が１ になるように正規化すると、
のようになりますが、ここでは正規性はあまり本質的でなく、式表現も複雑になるので、定数倍
を繰り返して、
のように一次結合で表したとします。 すると、各係数は信号
であり、級数展開は
のような形になります。
どのような信号の集合が、フーリェ級数展開で表現可能（完備）でしょうか？ 実は、この質問に答えることは大変難しいことです。 というのは、今までの議論で、断りなしに、等号（＝）を用いて話を進めましたが、この等号は、どの時刻
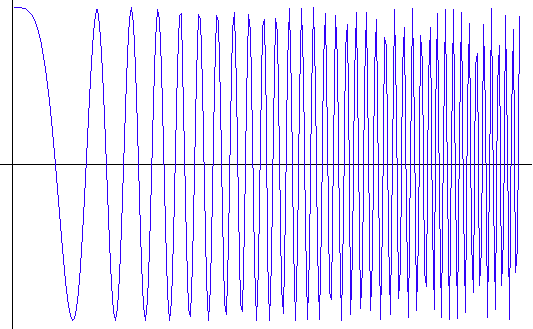
上のような信号は、ちょっと後回しにしましょう。 実用上、上のような信号を扱うことは絶対ありません。 どんなに発散しても、無限に大きくなってしまう信号なんて実現することはできません。 また、信号が瞬間的にジャンプしているようでも、ズームインしてみれば連続的に繋がっているはずです。 そんなわけで、連続信号について、級数展開が等号の意味で可能かどうかをまず確かめてみましょう。 それでも未だ、連続性だけでは非常に困難なケースが予想されます。 たとえば、広く使われている下図のようなチャープ信号 ( chirp signal ) があります。
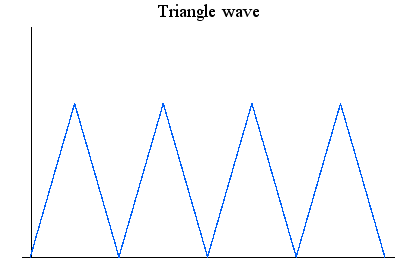
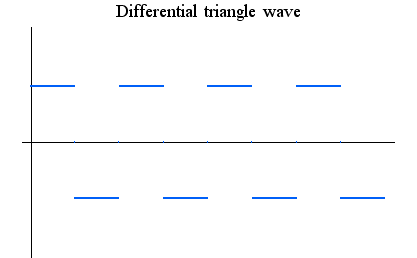
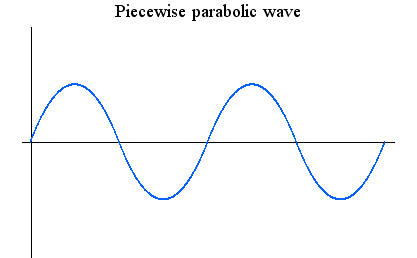
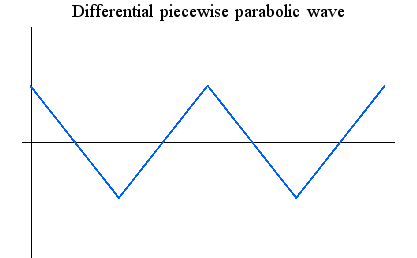
有限時間内に低周波から高周波まで周波数をスイープしますが、この極限として無限に高い周波数までを有限時間内にスイープする状況を考えると、最初は連続だけれど、区間の終端で、連続性が怪しくなってきます。 このような信号も対象から除きたいのですが、その条件を「滑らかさ」で定義しまよう。 「滑らかさ」を、「全時間にわたって連続で有界、かつ、その１回微分もまた連続であり有界」としてみます。 そうすると、まず上のスイープ信号の微分は区間の終端で発散しますから排除することができます。 加えて、下図のような三角波形の微分は角のところで不連続になるので、これも除かれます。 もし下図のように、三角波形の角が２次曲線で丸めて、２次曲線と直線の接合点で微分が連続になるようにすれば、上で定義した「滑らか」の範疇に入ります。
注１：点と点を曲線でつなぐ問題を一般に内挿 (Interpolation) といい、多くの工学分野で重要な技術です。 上の考え方のように、接合点で１次微分を（場合によっては、２次微分や３次微分なども）一致させて多項式の断片をつないで作った滑らかな関数をスプライン関数 (splineは自在定規あるいは雲形定規)といっています。 まず、前述を繰り返しますが、展開係数
そして、この「距離」を最小にする
このようにして、
が言えなければなりません。 詳しいことは数学の参考書に任せるとして、大筋は以下のようです。
上の二つは、独立に導くことができます。 もし、対象としている工学的課題が、最初から最後まで自乗誤差積分を評価して完結するならば、
最後に、信号に不連続点を許した場合については、まず不連続点が有限個と仮定します。 もし、無限個の不連続点を許すと、たとえば、どんな微小区間をズームアップしてもとびとびの値をとるような信号も対象に入り、フーリェ展開が不可能になります。 有限個の不連続点をもち、それ以外では滑らかな信号について以下がいえます。
注３：工学的には、有限項で打ち切ったフーリェ級数展開が重要な意味をもちます。 とくに、不連続点あるいは連続であるが急激に変化する近傍で、どのように近似が行われるかは重大な関心事です。 この近似の様子を端的に示す現象がギップス現象（Gibbs’ phenomenon ） です。 注４：周期的でない信号の周波数分析については周波数分析を参照してください。 注５： 信号が確率過程であるときの直交展開については、Karhunen-Loeve expansion を参照。
|
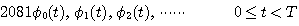
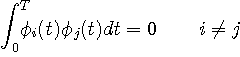
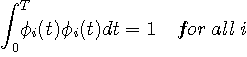
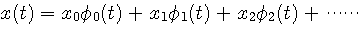
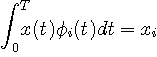
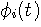の係数
を与えます。 このようにして、信号に含まれる直交成分の大きさを個別に知ることができます。 このことが、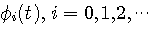
が直交条件を満たしている大切な意味です。
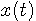について、上の内積を、
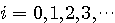と無限に実行して得られる級数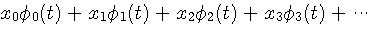
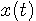を与えなければ意味がありません。 もし、Ｓ の中に 
, 
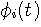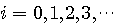と直交する成分が含まれていると、いくら分析してもその成分は発見できないわけです。 以上が直交分解の概略のストーリーです。 ここで問題は
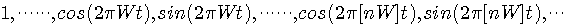
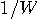秒の周期関数です。 したがって、基本周期区間
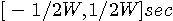に入る部分だけを取り出して考えれば十分です。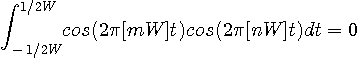 
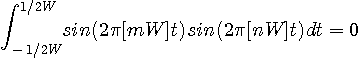
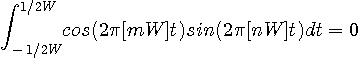
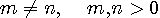
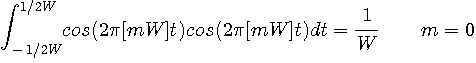
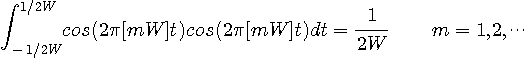
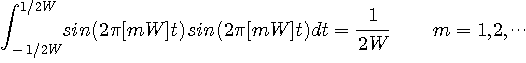
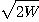
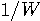秒の信号 
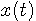を内積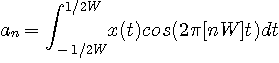
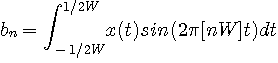
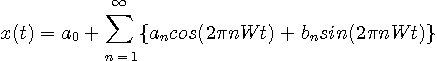
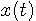に含まれる周波数成分の大きさを与えます。 たとえば、
、
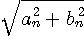
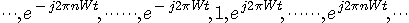
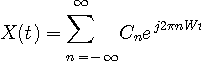
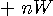
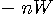
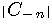
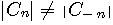です。 周波数には正と負があることについては
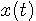に収束することを意味しなければなりません。 こう考えると、いろいろな心配が出てきます。 たとえば、下図のような信号は、等号の意味で級数展開できるかどうか心配です。 それぞれの三角関数は連続関数ですから、それらを無限個用いて不連続な信号が等号の意味で合成できるかどうかはただちに結論できません。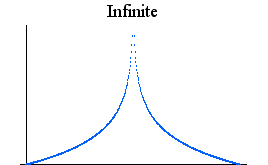
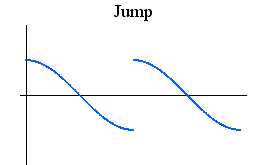
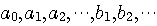
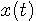と N次展開 
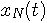との「距離」を次のように定義します。
, 
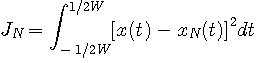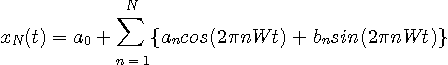
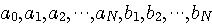を決めることにします。 この計算は、上の左側の式に右側の式を代入し、それぞれの係数
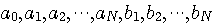で偏微分した結果をゼロとおいて得られますが、連立方程式を解くまでもなく、直交性から個別に以下の内積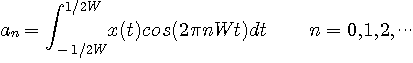
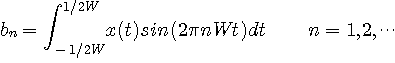
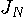を最小にするような展開法をフーリェ級数展開といい、展開された係数をフーリェ係数といっているわけです。 こうして求めたフーリエ級数が、
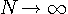のとき本来の等号の意味で信号 
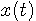に収束するか否かを明らかにしたいわけです。 そのためには、
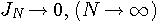を保証すること
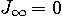が等式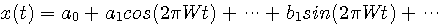 
を保証すること
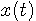が含まれるカテゴリー
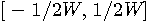で連続（滑らかでなくてよい）かつ有界であり、区間の両端において
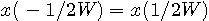とすると、任意の 
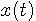に対して、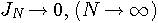
がいえる。 この収束
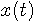に収束するかどうか分からないが、とにかく自乗誤差の積分をゼロにすることがきる。
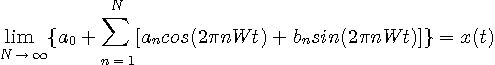
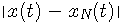が時刻に関係しない小さな値よりも小さくできる）と呼んでいる。
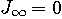だけを扱えば済みます。 もっと厳密に、等号の意味で収束が必要ならば、微分連続性が必要になります。 ただし、上では便宜上、区間全域にわたって微分連続性を仮定していますが、実は、区分的に微分が連続（微分の不連続点が有限個）であれば、元の信号の連続性から上のことが導かれます。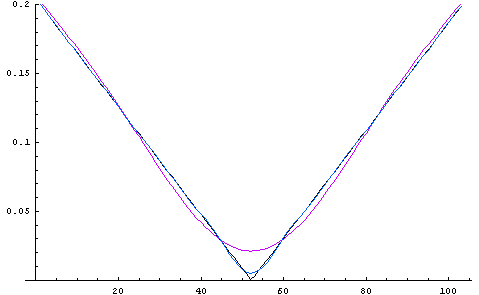
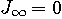の意味で収束する。 ただし、一回微分は区分的に連続とする。