|
1970年ごろ、私が目にしたソナグラムは、感熱紙を巻いたドラムが回転し、音声の短時間スペクトルを濃淡で記録するものでした。アナログの帯域フィルタがいっぱい詰まった大きな装置でした。我々の耳の構造も、このような周波数分析をしています。
短時間スペクトルは次のように表現できます。
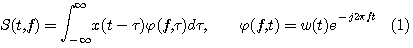
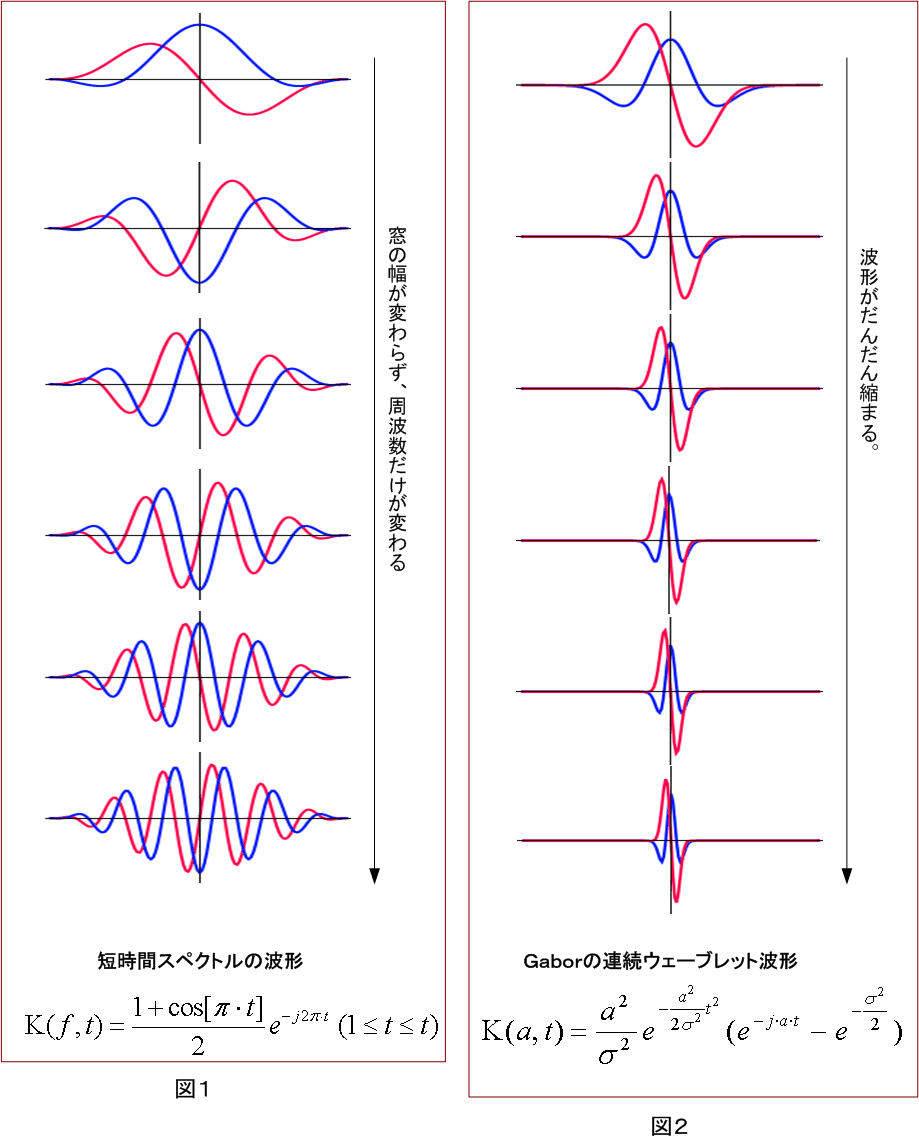
時々刻々、信号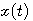 を窓関数 を窓関数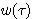 で切り取り、この波形をフーリエ変換するという意味をもっています。図1は周波数を変えたときの様子ですが、観測幅(窓関数の幅)が周波数によって不変であることが特徴です。 で切り取り、この波形をフーリエ変換するという意味をもっています。図1は周波数を変えたときの様子ですが、観測幅(窓関数の幅)が周波数によって不変であることが特徴です。
一方、ウェーブレットは、高周波へ行くにしたがって、観測幅を狭くすることが特徴です。そして、この特徴を一つの関数の伸縮だけて与えます。下式のように、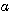 で観測幅の伸縮を変え、 で観測幅の伸縮を変え、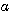 が大きいほど観測幅が狭くなります。 が大きいほど観測幅が狭くなります。
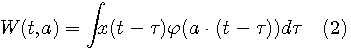
このような観測ができるためには、 ①任意の伸縮に関してウェーブレットが2乗可積分であること、 ②ウェーブレットは直流成分を含まないこと、が必要です。
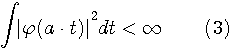
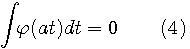
ここで、式(2)の左辺 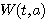 から、元の信号 から、元の信号 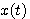 を求める逆変換ができるためには条件が必要です。これについては、デルタ関数のページを参照してください。もっとも古典的なGaborのウェーブレットを図2に示します。青色は実部、赤色は虚部です。 を求める逆変換ができるためには条件が必要です。これについては、デルタ関数のページを参照してください。もっとも古典的なGaborのウェーブレットを図2に示します。青色は実部、赤色は虚部です。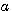 に比例して、観測幅が狭くなっていきます。時間軸と周波数軸の観測幅を同時に小さくすることはで来ません(不確定性原理)。 に比例して、観測幅が狭くなっていきます。時間軸と周波数軸の観測幅を同時に小さくすることはで来ません(不確定性原理)。
Gaborのウェーブレットは伸縮を連続的に変化できますが、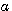 と と 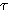 を離散化して、信号を効率良く表現する目的には、直交展開の保証がなく不向きです。離散化するには、関数の族 を離散化して、信号を効率良く表現する目的には、直交展開の保証がなく不向きです。離散化するには、関数の族
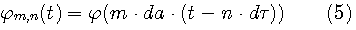
が互いに直交し、かつ、それらの一次結合で、ほとんどの信号が表現できなければなりません。時間シフト幅は周波数の観測幅に反比例するので、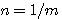 とし、更に、伸縮のルールを2のベキとし、 とし、更に、伸縮のルールを2のベキとし、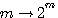 と書き直すと、式(5)は次のようになります。 と書き直すと、式(5)は次のようになります。
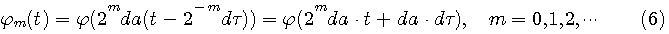
さて、式(6)のような形をした完備な直交関数系はあるでしょうか? この問題に最初に解答を出したのが Carsten Mayer (1968年、ドイツ 生まれ)でした。その関数の導出はマニアックなので、図3に図解します。
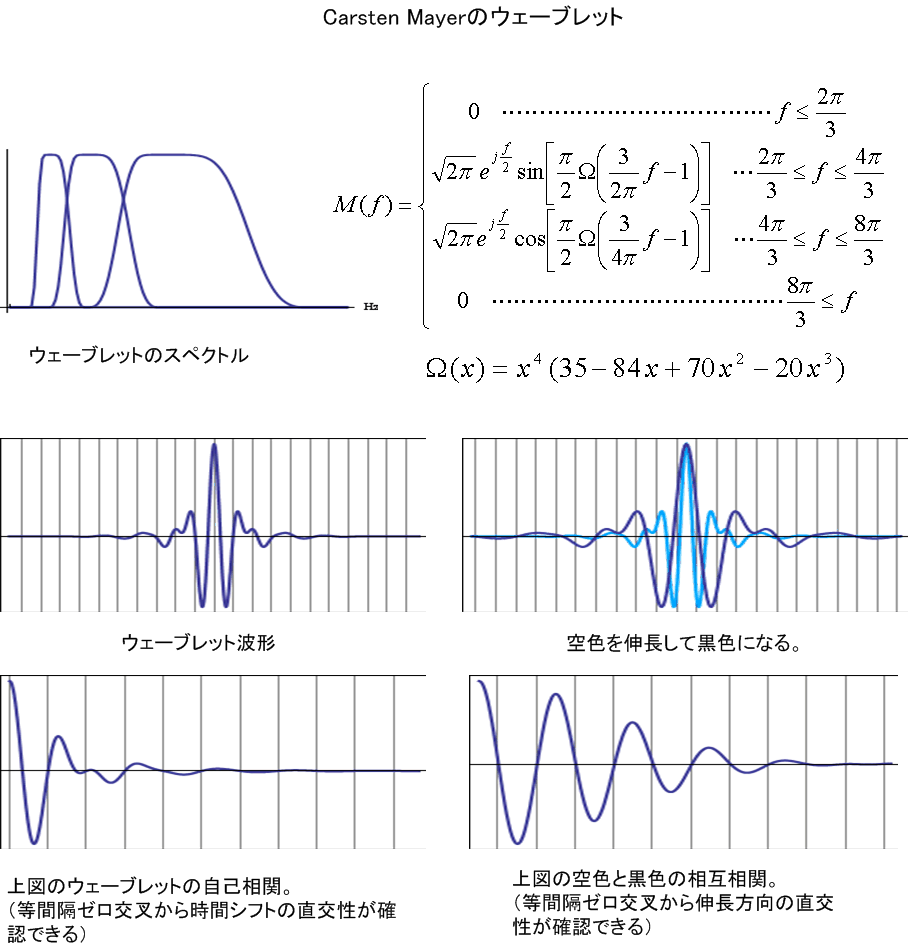
図3
離散ウェーブレットは、馴染み深い短時間スペクトルと異なり、その結果を見て信号の物理的性質を引き出すことは困難です。図4の音声波形に対する短時間スペクトルとMayerの解析結果を図5に示します。
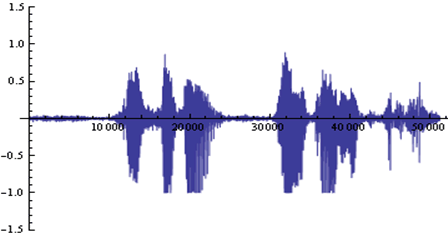
図4
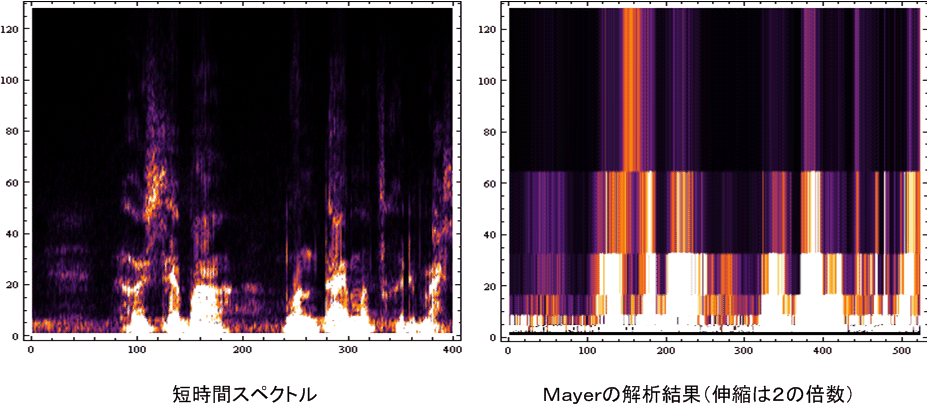
図5
ウェーブレットについて、革新的なアイデアを出したのは、Ingrid Daubechies (1954年、ベルギー 生れ)です。その特長は、有限サポート(ウェーブレットの長さが有限)であり、その構成法が再帰的で、計算プログラムが極めて簡単なことにあります。まさに、計算機時代のスマートな方法です。以下に、構成法の原理を説明します。
スケーリング関数を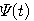 で表し、これへの伸長( で表し、これへの伸長(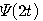 から から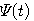 へのdilation)が4つの時間シフト(偶数なら4以上でもOK!)の一次結合で与えられるとします。なお、一般性を失わないので、 へのdilation)が4つの時間シフト(偶数なら4以上でもOK!)の一次結合で与えられるとします。なお、一般性を失わないので、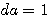 、 、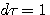 としました。 としました。
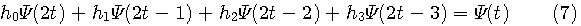
この式を満たす有限サポートの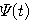 、そして、そのウェーブレットを設計することがテーマです。 、そして、そのウェーブレットを設計することがテーマです。
設計手順を、次のように2段階に分けます。
式(7)を満たすスケーリング関数 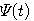 が存在するとして、ウェーブレットの要件を満たす 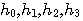 を求めます。 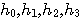 から、式(7)を満たす 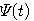 を再帰計算で求めます。この再帰計算はウェーブレットに関係のない一般的手法です。
まず第1段階では、次の4つの要件を満たす 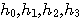 を求めます。 を求めます。
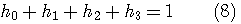 これは、 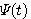 のスペクトルの直流成分を1に固定することを意味しています。 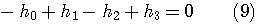 スケール関数 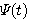 から、ウェーブレットを 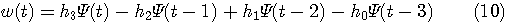 で定義したとき、ウェーブレットの直流成分がゼロであることを要求しています。このウェーブレットの定義から、伸縮方向の直交性が保証されます。これについては、後で図解します。 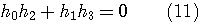 ウェーブレットを2時刻間隔でシフトします。このときの、時間シフトの隣接との直交条件です。 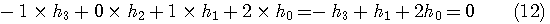 左辺は時間原点を 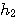 の位置にしたときの一次モーメントで、ウェーブレットの周波数特性の微分を意味しています。この条件は、周波数特性の微分が直流においてゼロであることを要求しています。物理的に言えば、ウェーブレットのスペクトルの帯域通過性(チューニングの強さ)を要求しています。
式(8)、(9)、(11)、(12)の連立システムから、スケーリング系列が次のように得られます。
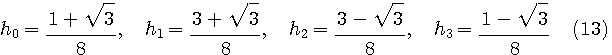
この係数の定数倍(分母の8など)は本質的ではありません。再帰計算の中に正規化操作を挿入すればよい。 さて、条件2の式(10)の定義はちょっと奇妙ですが、これによってウェーブレットの伸縮方向の直交性を保証することができます。文章で説明するとイメージが湧かないので、下の図解で直感的に理解してください。
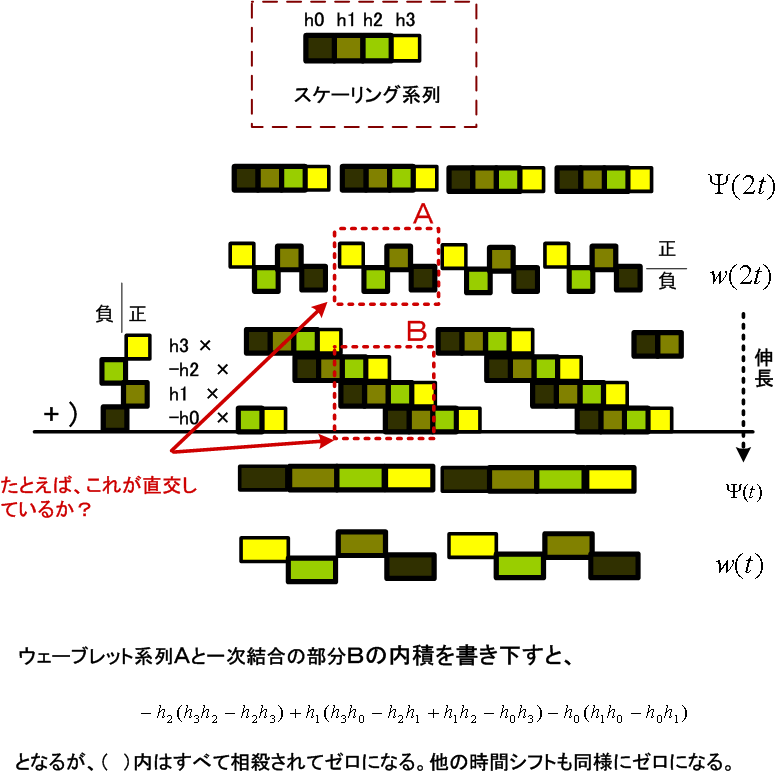
図6
第2段階のスケーリング関数を求める再帰計算を説明します。計算に先立ち、最も長いスケーリング関数のシフト間隔を決めます。ここでは、128とします。以下は再帰計算の手順です(計算過程は図9を参照)。
- まず、
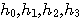 の間に、ゼロを127個挿入する。 の間に、ゼロを127個挿入する。

この系列の右側に、長さが1024になるまでゼロを追加し、FFTする。この結果を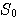 で表す。 で表す。 とする。 とする。
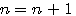 とする。 とする。 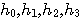 の間に の間に 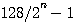 個のゼロを挿入する。 個のゼロを挿入する。
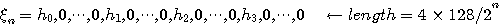
この系列に、長さが1024になるまでゼロを追加してFFTしたものを 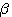 とする。 とする。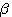 と と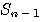 との積を求め、これを との積を求め、これを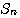 とする。 とする。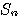 の直流値が1になるように正規化する。 の直流値が1になるように正規化する。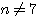 ならば、2へ戻る。 ならば、2へ戻る。 ならば、 ならば、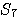 が求まっているので、これをIFFTしてスケーリング関数を出力する。 が求まっているので、これをIFFTしてスケーリング関数を出力する。
この再帰演算は、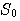 を を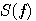 で表したとき、スケーリング関数のスペクトル で表したとき、スケーリング関数のスペクトル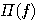 を、 を、
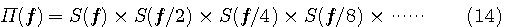
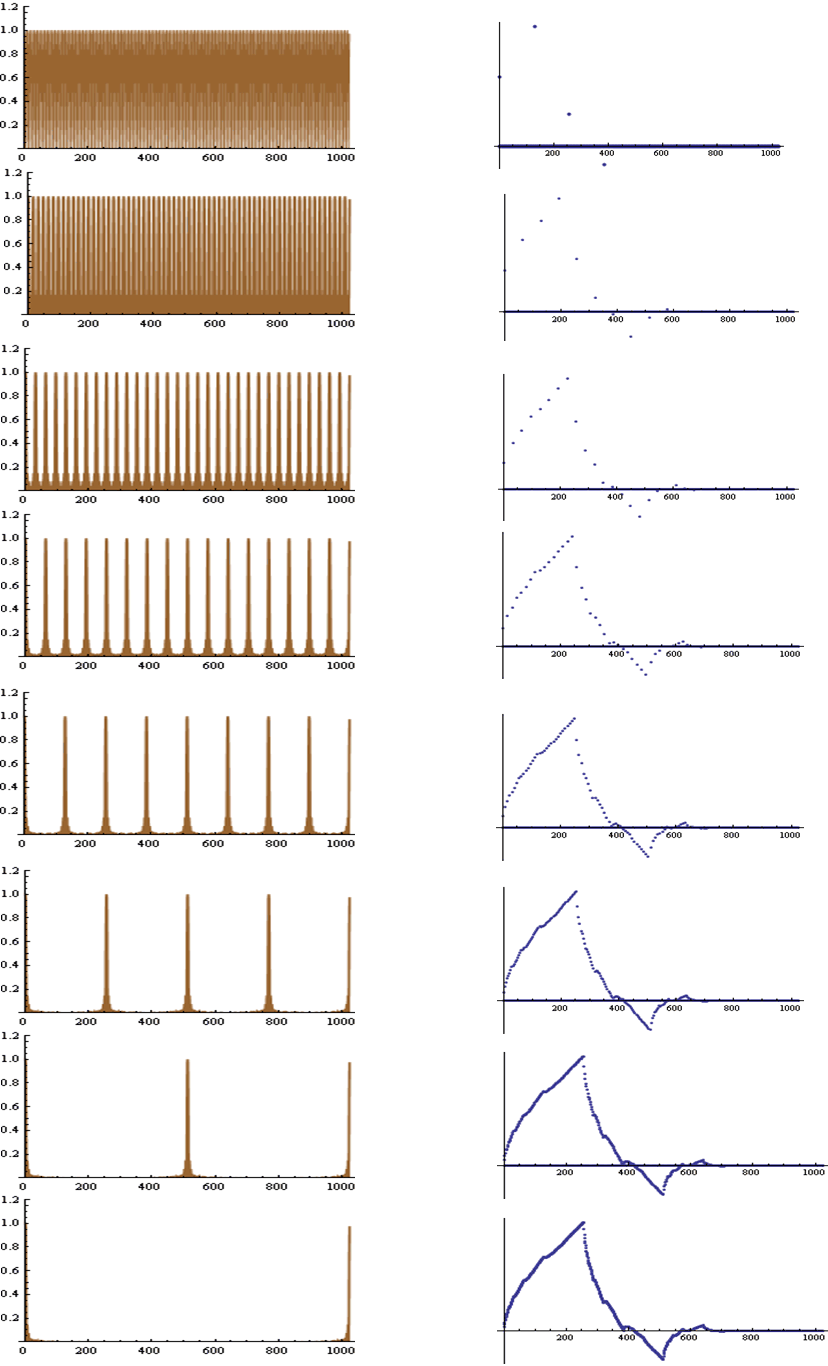
で求めることに相当します。上のステップ3で正規化されるので、数値的に発散しないで求まります。この再帰計算の結果は(ウェーブレットから離れて!)、初期関数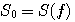 の4つの数列(4次FIRフィルタ)によって、非常に連続性が高いものや、ほとんどランダムなものに収束します。この操作は、内挿をだんだん細かくする意味をもっているので、ローパス特性が強い数列を選べば、連続的な関数に収束します。例えば、 の4つの数列(4次FIRフィルタ)によって、非常に連続性が高いものや、ほとんどランダムなものに収束します。この操作は、内挿をだんだん細かくする意味をもっているので、ローパス特性が強い数列を選べば、連続的な関数に収束します。例えば、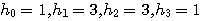 として上の再帰演算を実行すると、図7のようなカーブが得られます。また、 として上の再帰演算を実行すると、図7のようなカーブが得られます。また、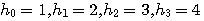 としてみると、図8のように、ほとんど連続性が認められません。 としてみると、図8のように、ほとんど連続性が認められません。
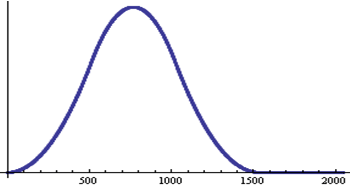 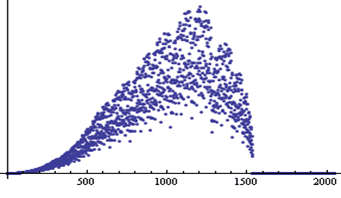
図7 図8
式(13)のDaubechiesの数列からスタートした結果(スケーリング関数とウェーブレット、そして、ウェーブレットの直交性の確認グラフ)を以下に示します。式(13)の数列はランダムな関数へ収束しそうな気配ですが、最後のモーメントの条件が連続性にかろうじて効いているようですね。図9に計算過程を示します。
なお、式(14)を
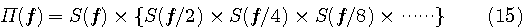
のように表現すると、 の中は の中は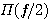 なので、スケーリング関数の伸長は なので、スケーリング関数の伸長は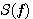 を掛けることになります。Daubechiesでは、 を掛けることになります。Daubechiesでは、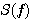 は4つのインパルス列なので、図10のような簡単な畳み込み計算になります。 図11はウェーブレットの直交性の数値的確認です。 は4つのインパルス列なので、図10のような簡単な畳み込み計算になります。 図11はウェーブレットの直交性の数値的確認です。
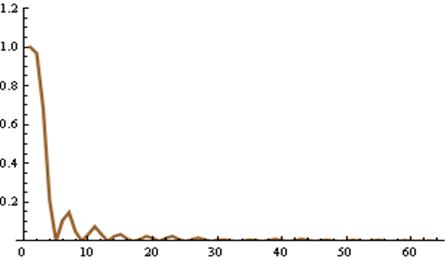
(左側一番下のスペクトルの拡大)
図9 再帰計算の過程を示す図
(左側が式(15)の途中結果、右側はそのIFFTのスケーリング関数です)
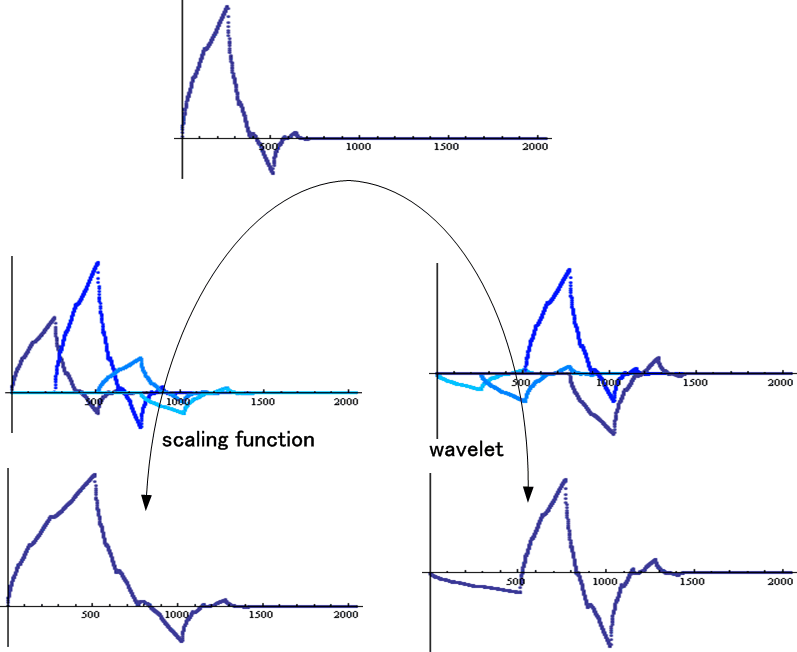
図10 図の一番上のスケーリング関数から、その伸長とウェーブレットを得る操作
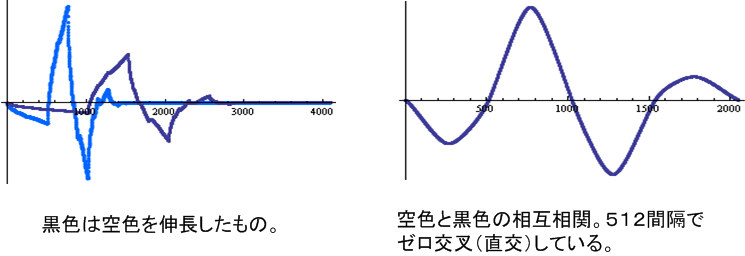
図11 伸長方向にあるウェーブレットに直交することの数値的確認。
|


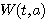 から、元の信号
から、元の信号 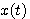 を求める逆変換ができるためには条件が必要です。これについては、
を求める逆変換ができるためには条件が必要です。これについては、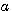 に比例して、観測幅が狭くなっていきます。時間軸と周波数軸の観測幅を同時に小さくすることはで来ません(
に比例して、観測幅が狭くなっていきます。時間軸と周波数軸の観測幅を同時に小さくすることはで来ません(



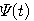 で表し、これへの伸長(
で表し、これへの伸長(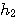 の位置にしたときの一次モーメントで、ウェーブレットの周波数特性の微分を意味しています。この条件は、周波数特性の微分が直流においてゼロであることを要求しています。物理的に言えば、ウェーブレットのスペクトルの帯域通過性(チューニングの強さ)を要求しています。
の位置にしたときの一次モーメントで、ウェーブレットの周波数特性の微分を意味しています。この条件は、周波数特性の微分が直流においてゼロであることを要求しています。物理的に言えば、ウェーブレットのスペクトルの帯域通過性(チューニングの強さ)を要求しています。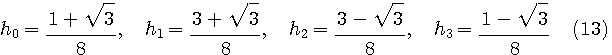

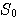 で表す。
で表す。 とする。
とする。

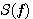 を掛けることになります。Daubechiesでは、
を掛けることになります。Daubechiesでは、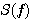 は4つのインパルス列なので、図10のような簡単な畳み込み計算になります。 図11はウェーブレットの直交性の数値的確認です。
は4つのインパルス列なので、図10のような簡単な畳み込み計算になります。 図11はウェーブレットの直交性の数値的確認です。


