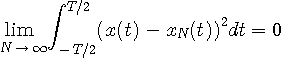|
ギッブスの振動 Gibb's oscillation |
|
下図のような周期
のようになります。
ギップス(Josiah
Willard Gibbs,
1839-1903)は不連続点の近くの
を満たす一番小さな時刻で生じます。 右辺カッコ内の各項は余弦関数を等間隔にサンプルしたものですから、半周期を(
となります。 実際、上の{
}の中は項数
を満たすことは明らかです。 しがって、この時刻を
のように求まります。 項数
N=5 1.18233 ギッブスの現象は、フーリェ級数がすべての時刻で一様に収束するのではなく、自乗誤差の積分
の意味で
|
 秒の繰り返しパルスに対して、フーリェ級数展開がどのように近似するかを調べてみましょう。
秒の繰り返しパルスに対して、フーリェ級数展開がどのように近似するかを調べてみましょう。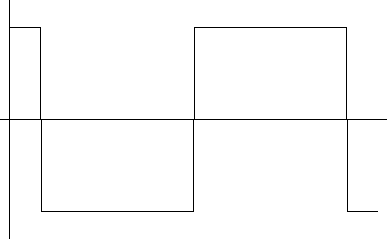
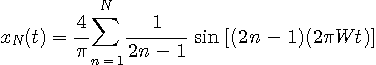
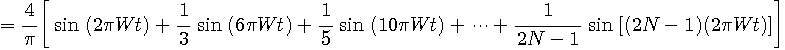
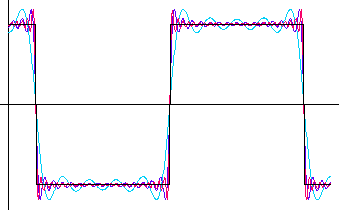
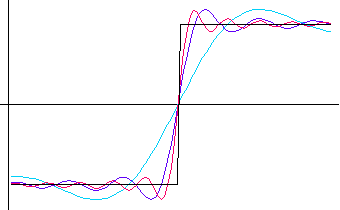
 を選べばそれが最小です。 その時刻は
を選べばそれが最小です。 その時刻は