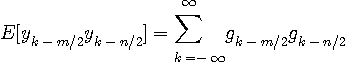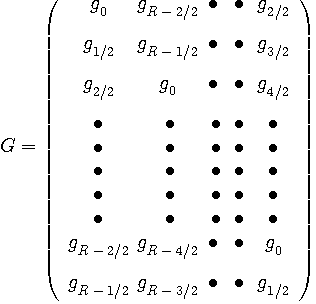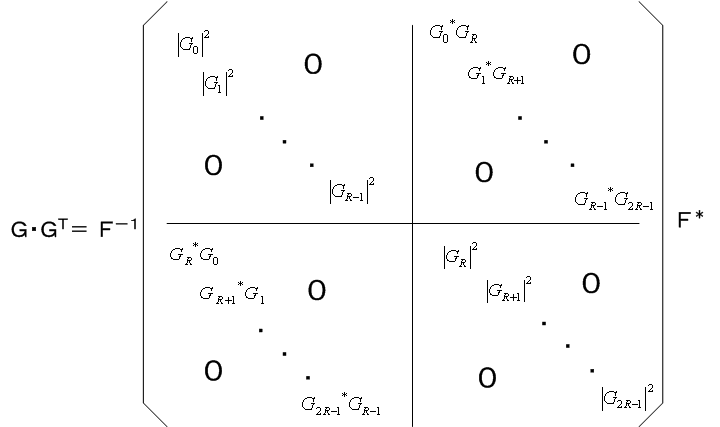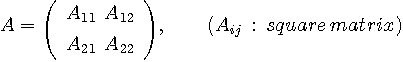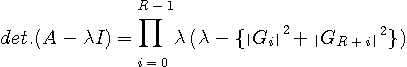|
最小自乗平均等化の解 Solution of mean square equalization |
|
等化出力
を最小にする等化法を「最小自乗平均等化」と呼ぶことにします。 シンボルレート等化 と ダブルサンプリング等化 について、上の評価関数を最小にする解の性質を調べます。 この最小化問題を形式的に解くだけでは、物理的意味合いが分かりにくい恐れがあるので、次の方針で調べます。 (1) まず、雑音なしとします。 送信シンボルを周期的とし、タップ長をこの周期に等しくした場合について、シンボルレートとダブルサンプリングの解を調べます。 このような等化を「サイクリック等化」と呼んでいます。 サイクリック等化では、離散フーリエ変換で正確な解の表現が得られるので、シンボルレートとダブルサンプリングの性質を明瞭に説明することができます。 周期を十分長くすれば、非周期でタップ数が十分多い場合の解に近似します。 (2) 上の考察に、加法的有色ガウス雑音を追加します。 そして、シンボル周期とタップ長を無限に長くしたとき、等化器が到達する解が最適受信フィルターを実現するかどうかについて検討します。 ただし、送信シンボルはランダムとします。 (3) 雑音なし、ランダム送信シンボル(非周期)、有限長等化器を仮定して解を求め、サイクリック等化とのアナロジーを理解します。 以下、この三つの方針にそって説明を進めます。
(1)雑音なし、サイクリック等化
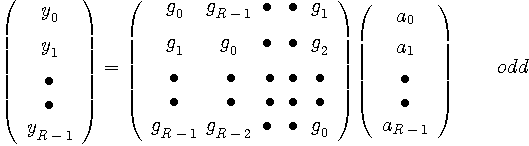
ここで、行列は巡回行列であることに注目してください。 すなわち、第1行、第2行、・・・・の順に、
式(*)は、周期的なシンボル系列と周期的なパルスとのコンボリューションを表していますが、これは離散フーリェ変換で表すと簡単になります。 すなわち、
とすると、
のようになります。 さらに、これを同じ長さのシンボルレート等化器に入力したとき、離散フーリェ変換による入出力関係は次のようになります。
ここで、
ですが、その離散フーリェ変換は一致するので、この関係から代入操作を繰り返すと、
のように導かれ、右端の等化目標に到達します。 次に、ダブルサンプリング等化の離散フーリェ変換による等化プロセスを導きます。 ダブルサンプリング等化器の入力は受信信号を倍のスピードでサンプリングしたものです。 1周期分のサンプル数は2R個ですから、これを要素とする2R次元受信ベクトルはR次元の送信シンボルベクトルに2R行R列行列を掛けて得られます。 この変換を離散フーリェ変換で表現するとどうなるでしょうか? 上の行列の構造をみると、第1行、第3行、第5行と、奇数番目の行ベクトルを選んでできるR行R列正方行列は式(*)の行列と同じです。 一方、偶数番目の行ベクトルを選んでできるR行R列正方行列は上図のオレンジ色のサンプル系列から作られるものです。 したがって、奇数番目と偶数番目の二つに分割すると次のように表せます。
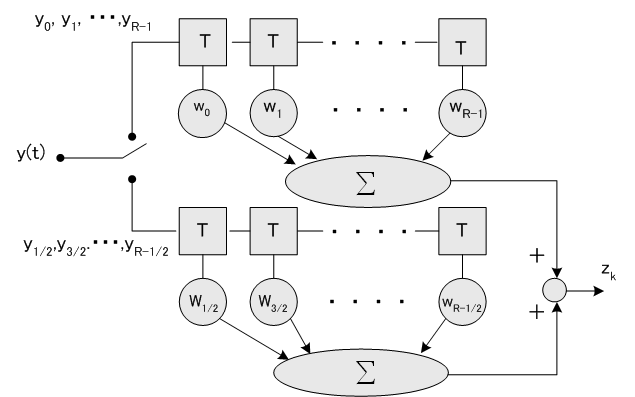
ダブルサンプリング等化はこれらを別々に等化して加算したものです。 この操作を描くと下のブロック図のようになります。
離散フーリェ変換による表現は次のようになります。
ブロック図の上と下のシンボルレート等化器から出力される信号の離散フーリェ変換は次のようです。
結局、等化目標は、
のように導かれ、もし
が等化目標となります。 ダブルサンプリング等化がサンプリング位相によらず、常に等化可能であるということは、すべての
実信号の場合は、ちょうど、
ですが、右辺の構造をみれば、
(2)加法的有色ガウス雑音、送信信号の電力スペクトルは平坦、非周期
一般に、
( のようになります。 この公式を用いて、
最適受信フィルターは基本的にはアナログフィルです。 したがって、シンボルレート等化器だけでは最適受信フィルターになることはできません。 一方、ダブルサンプリング等化器は、もし受信信号の帯域幅が2/T Hz以下(ロールオフ率が100%以下)であれば、標本化定理を満たしているので最適受信フィルターを満たす能力があります。 実は、上の連立方程式から最適受信フィルターの条件式を次のように導くことができます。 まず、連立する二つの式を次のように書き換えてみます。
( )内の
と同等になることがいえます。 以上から、ダブルサンプリング等化は有色雑音に対して理論的最適を実現することがいえました。 ただし、最適を実現する有効な等化アルゴリズムがあるかどうかは別問題です。 これに関しては最急降下等化アルゴリズム、高速収束法を参照してください。
(3)雑音なし、非周期送信シンボル系列、有限長等化器
のように分解できます。 この評価関数の極値は、各タップ係数の偏微分をゼロと置いた連立一次方程式を解いて得られます。
のような変形からわかります。 すなわち、
になります。 ここで 次に、ダブルサンプリング等化の解について調べますが、これはシンボルレートのベクトルと行列の定義を変えるだけで、上の筋道をそのまま繰り返せば済みます。 評価関数の分解は次のようです。
ベクトル
この場合の相関行列 ちなみに、ダブルサンプリングの行列
ですが、これから演繹してサイクリック等化の
とその転置の積
になることが分かります。 計算過程は省きますが、上の式は離散フーリエ変換を用いて次のように変形できます。
右辺の真ん中の行列は4つのR次元対角行列のブロックからなっています。 この行列の固有値は、右上と左上のブロックがじゃまをして、対角項の電力スペクトル
の行列式は、
のように分解できます。 この関係式を適用して固有値を求めると、
となり、固有値の半数は正確にゼロ、残りの半数はシンボルレート等化の固有値と一致することが導かれました。 非周期のケースでも、タップ数が十分多い場合は、固有値の半数がゼロになってしまい、解は一意に定まらないことがいえます。
|
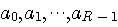 の繰り返しだったとします。 すると、受信信号をシンボルレートでサンプリングした系列も周期
の繰り返しだったとします。 すると、受信信号をシンボルレートでサンプリングした系列も周期
 の周期系列で、その関係は次のように表せます。
の周期系列で、その関係は次のように表せます。
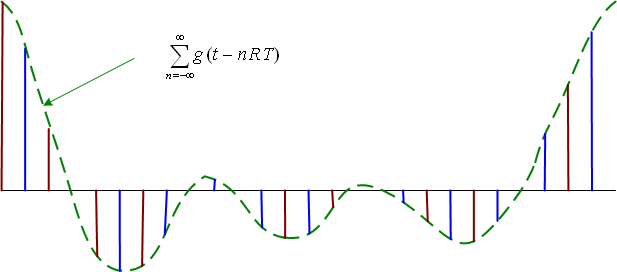
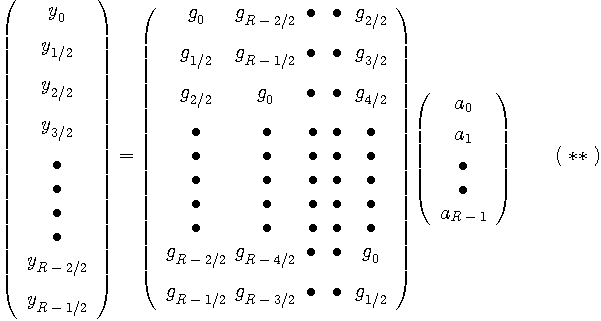
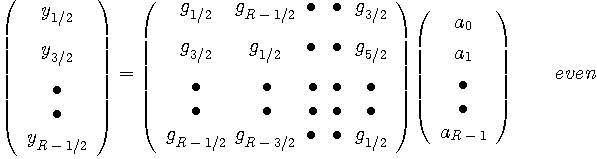
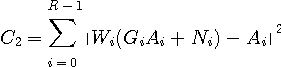
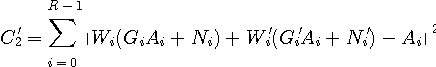
 に関して微分すると、
に関して微分すると、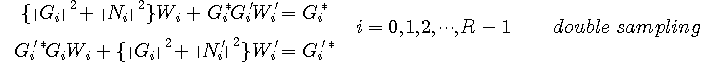
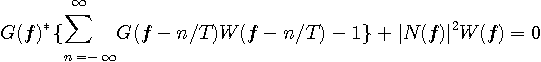
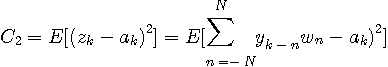
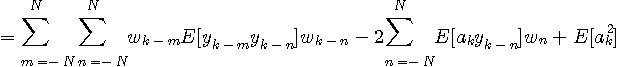
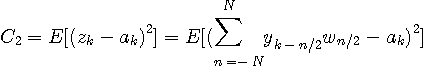
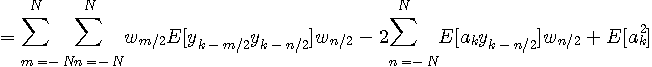
 の要素を
の要素を