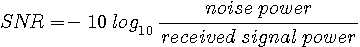|
最適受信フィルター Optimum receiving filter |
|
チャンネルの周波数特性と加法的ガウス雑音の電力スペクトルが与えられると、送信信号の電力スペクトルをどのような形状にしたとき、最小のロスで情報が伝達されるかという問題を解くことができます。 最適送信スペクトルは注水定理によって得られ、このときチャンネルは最大の能力を発揮し、これを通信路容量と呼び、チャンネル固有の量でした。 しかし、送信信号の電力スペクトルを最適な形に成形するか、あるいは何もしないか、それは実用においてさまざまです。 ここでは、何もしないで、すなわち、予め送信信号の電力スペクトルが決まっているものとし、これにチャンネル歪が加わったとき、受信信号にどのようなフィルターをかければ送信シンボルをもっとも正確に得るかという問題を考えます。
送信フィルターとチャンネル応答のコンボリューションをとって、二つの従属結合の応答を
最小化したい評価関数は
と書けます。 送信信号も雑音も定常確率過程とします。 そして、送信信号と雑音は発生源が異なるので互いに無相関とします。 すると、上式の
ここで、
が得られます。
となります。 さらに、雑音がなければ、簡単に
ですから、逆数が存在するか否かは別として、単にパルスとチャンネルからなる伝送システムの逆システムになります。 最適解を評価関数
以上はアナログ伝送の場合でしたが、ディジタル伝送の場合は導出がやっかいです。 ここでは結果のみを示します。 シンボル
評価関数
のようになります。 ここで、
のような陰形式で求まります。 残念ながら
厳密に最適ではないが限りなく最適に近い受信フィルターは次のようなテクニックで導出できます。 受信フィルターを、アナログフィルター
とすると、式(**)から、
のような表現を得ます。 ここで、
なお、雑音が有色の場合は、式(*)に遡り、
のような、もう少し最適な解が得られます。
このときの、評価関数
のようにちょっと複雑ですが、データがランダムかつ雑音が白色では、次のように簡単になります。
なる条件のもとで、
です。 注: 式(**)は、送信パルスとチャンネルからなる系の自乗周波数特性の周期的重畳が平坦であるとき、アイを最も開かせることを意味しています。 もし、式(**)が
高域で急速に減衰する線路で高速通信するケースでは、解(**)は単純に線路の逆振幅特性を送信側にもたせれば、ほぼ最適といえそうです。 例として、金属線通信のケースを当たってみましょう。 線路の振幅特性を
このときの
送信側でなにもしない場合と送信側で伝送路の逆特性をもたせる場合について、最適受信フィルターを通した後の自乗誤差
ついでに、赤色(e1)と黒色(e2)の比、e1/e2
をプロットすると下図のようになり、
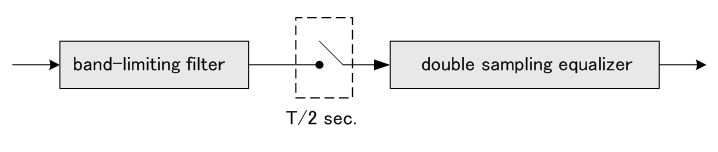
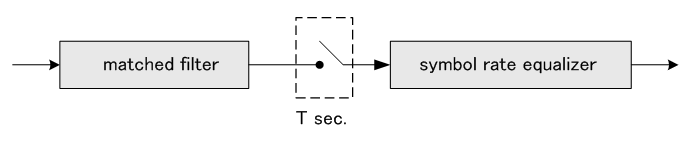
以上の結果から、シンボルレート等化器は、整合フィルターを前置すれば(実用ではあまり実施されていませんが)、ほとんど最適受信フィルターを実現するといえます。 一方、ダブルサンプリング等化器は、下図のように、受信信号の帯域幅を
|

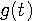 とします。
とします。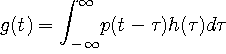
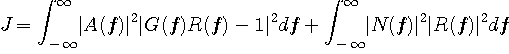
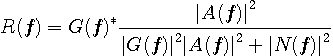
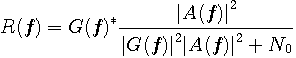
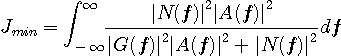

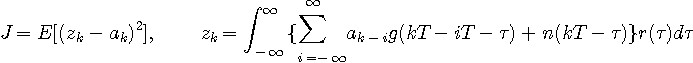
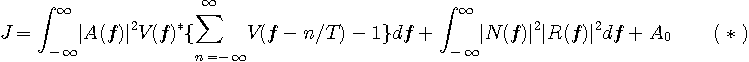
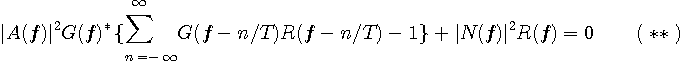
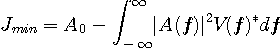
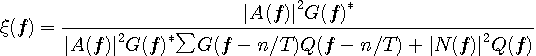
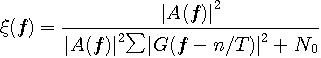
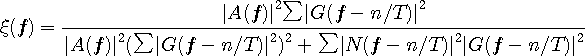
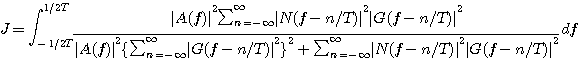
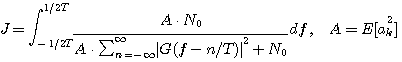
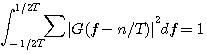
 をプロットすると下図のようになります。 赤色は前者、黒色は後者です。
をプロットすると下図のようになります。 赤色は前者、黒色は後者です。