|
情報を測る Metric of information |
|
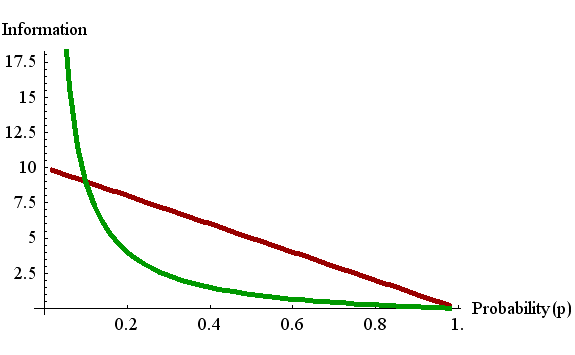
僕たちは、毎日のようにテレビを見たり、ラジオを聞いたり、新聞を読んだりしています。 このとき、 君はどれだけの情報を得たか、正確に答えろ！ なんて言われると困ってしまいすね。 ヘッ！ 情報って測れんの？ と、聞き返したくなりますね。 せいぜい、「たくさん」とか「ちょっとだけね」としか表現できないのではないでしょうか。 それも、人によってずいぶん違うでしょう。 でも、世は Ｉ Ｔ 時代！ ビット、ブロードバンド、インターネット、・・・・といった片仮名用語が氾濫しています。 なんだか、ものすごく工学的な匂いのする言葉ばっかりで、万事が精密に設計された世界をイメージしてしまいます。 そうです！テレビや携帯やパソコンやゲーム機やデジカメなど、すべての情報機器は、 情報を測る尺度 ： ビット を用いて設計されているのです。 ちょうど、メートルという長さの単位を使って家を設計するように。 炎天下、町内会の草むしりがありました。 今年は、「ご苦労さん」ということで、１０人の参加者に図書券をくじ引きで配ることになりました。 １等（１つ）： 図書券８枚 ４０００円相当 ２等（２つ）： 図書券４枚 ２０００円相当 ３等（３つ）： 図書券２枚 １０００円相当 ハズレ（４つ）： なし ぼくは、賭け事には弱く、くじを引いて良い思いをしたことは一度もありません。 でも、引いてみるとたった一枚しかない１等だったのです。 このときのぼくの「驚き」は、２等を引くよりも、また３等を引くよりも、もちろんハズレを引くよりも、大きいはずです。 上のクジは、この「驚きの度合い」を図書券の枚数で表しているようなものです。 図書券の代わりに、もっと理にかなった「驚きの度合い」を測る物差しはないでしょうか？もっと純粋に、あるいは体系的な議論ができるように、「驚きの度合い」を測りたいというわけです。 単純に考えれば、めったに起こらないことが起こったときほど「驚きの度合い」が大きいわけですから、「驚きの度合い」を確率の単調減少関数で定義すればいいわけです。 これだけならば、無数に定義を考えることができます。 そのことが起きる確率を
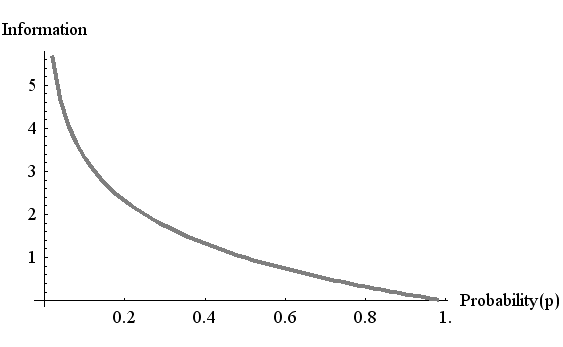
しかし、情報の大きさをこのような関数で表すと、後になって大きな不都合が生じます。 １９４８年、シャノン (C.E.Shannon, 、"A Mathematical Theory of Communication"1948、 PDF ) は情報を測る物差しを、２を底とする対数関数で定義しました。（ビット／秒を参照）。 確率p の事象が実際に起こったことを聞いたとき、
シャノンの定義式は連続的な実数値をとるので、一般に小数点以下が存在します。しかし、シャノンは、この単位を bits と名付けてしまいました。 この時代はディジタル時代の黎明期、一つのフリップフロップの回路は非常に高価でした。シャノンの論文の序章に、 『bits という言葉は J.W.Tukey （ＦＦＴを発表した彼はbinary digits をbits と略記していた） の示唆によるもので、一つのフリップフロップで表現可能な状態数は２であり、Ｍ個のフリップフロップを並べると表現可能な状態数は２のＭ乗になる。情報量を、状態数の２を底とする対数で定義し、bits で表す』 という記述がありまです。このことが、 ”bits は、"0"と"1"を並べた系列の長さの単位（非負の整数）” と思い込んでしまう混乱を後世に残すことになりました。 bits という複数形は整数をイメージします。 しかし、確率を導入すると、一般に情報量は非整数になります。 ＩＳＯやＪＩＳでは、この単位を Sh （シャノン） と記すように勧告していますが、まだ普及しているとはいえません。 ぼくたちのまわりには、上のような対数関数を使って大きさを評価することが非常に多いはずです。 一番ポピュラーなのはデシベル(dB)という単位です。 音や電気信号などのパワーを測るのに、
で計算します。 なぜ対数関数が便利なのでしょうか？ 対数関数で表す必然性はあるのでしょうか？ 対数関数とは関係
を満たす関数のことです。 もし変数が３つならば、同様に、
であり、変数の積の関数がそれぞれの関数の和になります。 このような関数を用いると、信号パワーを増幅したり減衰させたりする掛け算のプロセスを、積ではなく和で計算することができます。 このことが、広くデシベルが用いられている理由の一つです。 シャノンが情報量を測る尺度として対数関数を用いた理由はもっと必然です。 例として、Ａ、Ｂ、Ｃ の３文字をランダムに出力している情報源を考えてみよう。 ランダムとは、Ａ，Ｂ，Ｃ のどれが出力されるかは過去に出力された文字に依らないということです。 このような情報源のことを無記憶情報源と呼んでいます（過去の出力に影響を受けるような情報源はマルコフ情報源と呼びます）。 もし、Ａ と Ｂ と Ｃ の出力頻度に偏りがあり、仮に
とします。 シャノンの定義によれば、この情報源から Ａ が出力されたことを知ったぼくは
の情報を得ます。 Ｂ ならば
Ｃ ならば
の情報を得ます。 では、綴り ＣＢＣＡ を読んだとき、ぼくはどれだけの情報を得るでしょうか？ 情報源が無記憶だから、上の４文字の綴りが出力される確率は、それぞれの確率の積
であり、各アルファベットの情報量の和になります。 すなわち、長い綴りを読んだときの総情報量は、一つの文字を読むごとに、加算で蓄積された情報量に等しいことを表しています。 このように、 互いになんの関係もない情報を聞くたびに、 という原理はごく自然に理解できることです。 現実には、マルコフ情報源を扱うことが多いと思います。シャノンは、新聞の１ページに含まれる実質の情報量を測っています。英単語のアルファベットの並びには非常に強い相関があり、マルコフ情報源です。たとえば、q で始まる単語を辞書で引くと、かならず次に u が続きます。シャノンは、マルコフ性を持ったアルファベット単位の計算法を紹介した後、この計算法を捨て、単語を単位として英文の平均情報量を計算しています。単語単位（英単語の平均アルファベット数は４．５）ならば、その系列を無記憶情報源と見做せるという前提です。詳しくは、英文の平均情報量を参照してください。 注１：「確率ってな〜に？」と聞くと、その答えは十人十色ですね。 「サイコロを６００回振ったら一の目が１２０回出たので、一の目の出る確率は
120/600 だ」
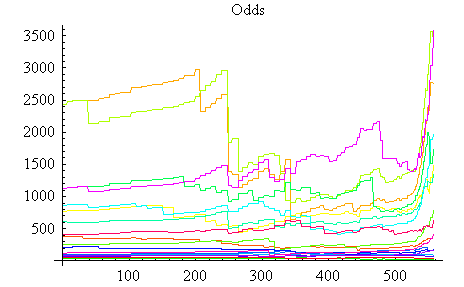
とか、「どの目も同じ可能性があるから 1/6 だ」とか、「サイコロの角が欠けるかもしれないから、確率なんて意味ないじゃん」とか・・・。 ぼくも、改めて質問されると大変困ります。 そういえば、ちゃんとしたサイコロは、重心を真ん中に置くために、目の彫りこみが微妙にちがっているよね。 注２：下図は競馬の１８頭単勝のオッズの時系列（配当金の時間変化）です。横軸は時間（分）、縦軸は配当金を表しています。この配当金は、ＪＲＡが総売り上げの一定率（２５％）を差し引き、残額を各馬の投票数の逆数に比例して配分した額です。この配当金は、「勝てない」度合いを表しているので、「勝ったときの驚きの度合い」といえます。
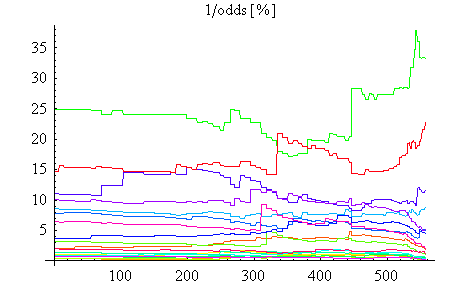
上のグラフで、人気馬（オッズの小さい馬）のオッズは非常に小さく、下にへばりついて判別できません。そこで、各馬のオッズの逆数のパーセント（投票数のパーセント）を描いてみると、人気馬の時間変化が表れ、不人気馬は下にへばりついてしまいます。このグラフは「人気の度合い」を表しているので、「勝つ確率」を意味しているともいえます。ただし、馬券を買う行為はギャンブルなので、「勝つ確率」をどの程度反映しているかは疑わしいですね。
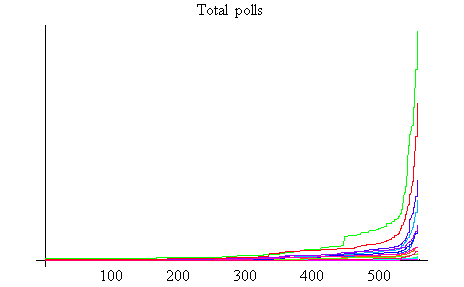
上のグラフから、投票累積の時間変化を推定することもでき、次のようになります。
この累積カーブから分かるように、締め切りの１時間前から投票が急速に増えることが分かります。締め切り時間に向かって、人間の欲望がどのように揺れ動くかを、これらのグラフから読み取れればおもしろい！ |
で表すと、例えば、
や 
は下の赤と緑のカーブのようになり、確率の単調減少関数ですから、確かに「驚きの度合い」を表現しています。なお、緑色のカーブの逆数は
は音波あるいは電気信号の強さを表します。 
で計算されます。 したがって、この綴りを読んだときの情報量は、
