|
対数関数 Logarithmic function |
|
下のように、変数の積の関数がそれぞれの変数の関数の和に分解されるような関数を対数関数といいます。
注: Logarithm のネーミングは、対数の発見者ネピア (John Napier 1550-1917) によるもので、ラテン語のロゴス(論理)とアリスモス(計算)を合成したものです。 ネピアと同世代に、ガリレオ (Galileo Galilei 1564-1642) やケプラー ( Johannes Kepler 1571-1630) がいます。 ネピアの問題は、”二つのボールを同じ初速度で飛ばす。一方は永遠に等速で飛び、他方は遠くの壁に近づくにしたがって、壁との距離に比例して減速する。 二つのボールの位置関係を計算したい” ということでした。 これは、近似的に対数(あるいは指数)関数を与えますが、当時の数学的背景からすれば、我々が理解している上の定義に至っていなかったようです。 なお、平山諦著「東西数学物語」によれば、「対数」という用語は、中国に宣教師が数表(常用対数表)を伝えたとき造られたということです。 「対」は「一組のもので、性質が異なる様子」を意味していますが、二列の数列に対して命名されたと思われます。 連続かつ微分可能な関数を仮定し、対数関数を
で表し、 では、(*)で示した定義だけから、対数関数がどのようなカーブを描くか調べてみましょう。
対数関数において、底を10に選んだものを常用対数と呼び、底を
に選んだものを自然対数(単位はネピア)と呼んでいます。 情報理論では底を2に選び、ビット(BIT)という単位をつけます。 実際に自然対数 の曲線を Mathematica でプロットさせてみると下図のようになります。
ついでに、この曲線を直線 に対称に折り返してみます。 この操作は
を作り出します。 下のような青い曲線になります。
この曲線は対数関数の逆関数になっているはずですが、これがどんな性質をもっているか調べてみます。 青色の逆関数を
ここで、
そして、
が得られました。 すなわち、対数関数の逆関数は、変数の和の関数がそれぞれの変数の関数の積に展開されることがわかります。 このような関数を
で表し、指数関数と呼んでいます。 上のグラフでは、底を e に選びましたが、一般に、逆関数は
のように表されます。 数学では底を
|
 で微分して、
で微分して、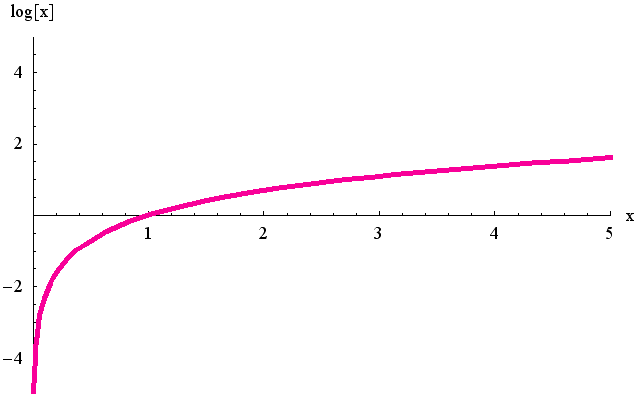
 と
と  を入れ替えた関数
を入れ替えた関数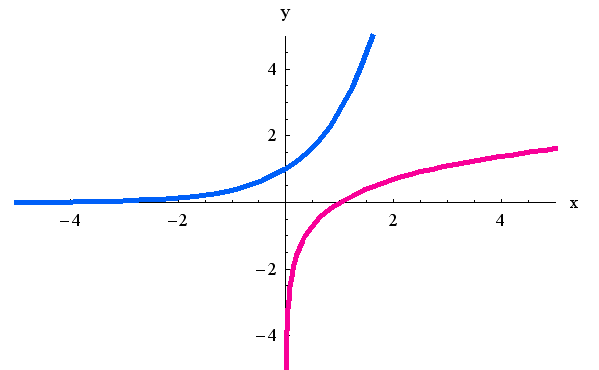
 に選ぶことが多いですが、その理由は、下式のように何回微分しても不変だからです。 底
に選ぶことが多いですが、その理由は、下式のように何回微分しても不変だからです。 底