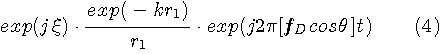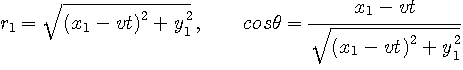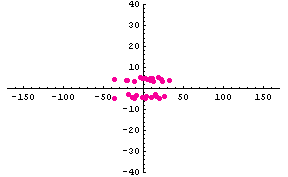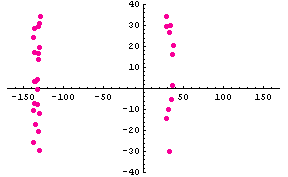|
��n�ǂ��甭�M���ꂽ�d�g�́A�s�X�̕��G�ȍ\�����ɂ���Ĕ��ˁE��܁E�U�����Čg�ђ[���ɓ��B���܂��B�@�g�ђ[�����ړ�����ƁA��n�ǂ���g�ђ[���ւ̓d�g�`�d�̗l�q���ω����܂��B�@���̕ω��͔��ɕ��G�ł���A���w�I���f�������ɂ͎v���������ۉ����K�v�ƂȂ�܂��B�@���̒��ۃ��f���́A�ȉ��̂悤�Ȃ��̂ł��B
- ��n�ǂ�������g��
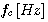 �̓d�g�����M����Ă���B���̓d�g�͔w�i�\���ŗ����˂����ʔg�ƂȂ��Ē[���ɓ���������̂Ƃ���B���Ȃ킿�A�S�����̖������_�ɖ����̔��M����z�肷��B �̓d�g�����M����Ă���B���̓d�g�͔w�i�\���ŗ����˂����ʔg�ƂȂ��Ē[���ɓ���������̂Ƃ���B���Ȃ킿�A�S�����̖������_�ɖ����̔��M����z�肷��B
- ��L���M�����烉���_���ȕ��f�U�������������f�����g
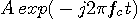 �����M�����B�@���Ȃ킿�A���f�U�� �����M�����B�@���Ȃ킿�A���f�U�� 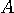 ���m���ϐ��Ƃ���m���ߒ����l���邱�ƂɂȂ�B�@�[�����猩�āA�ǂ̕����̔��M�����m���I�ɋψ�Ƃ���B ���m���ϐ��Ƃ���m���ߒ����l���邱�ƂɂȂ�B�@�[�����猩�āA�ǂ̕����̔��M�����m���I�ɋψ�Ƃ���B
- ��Ԃ͒�ݔg�Ŗ�������A���̒��w�����A���e�i���������[������葬�x�ňړ����A�u�Ԃɂ����Ď�M����ł��낤�M���̓d�̓X�y�N�g�������߂�B�@�d�̓X�y�N�g���͕��f�U�����m���ϐ��Ƃ��ċ��߂���B�@����������A���M�����قȂ�Β�ݔg�̗l�q���قȂ�A���ׂẲ\�Ȓ�ݔg���l�����Ď��g�������̃p���[�̊��Ғl���v�Z����B
- ���̓d�̓X�y�N�g�����t�[���G�ϊ�����Ύ��ȑ��ւ������A���Ԏ�����ԓI�����Ɋ��Z���Ēu���������ԑ��ւ�������B
�����̑O��̂��ƂŁA�d�̓X�y�N�g���͈ȉ��̂悤�Ɍv�Z����܂��B�@���}�̂悤�ɁA�\�������~����Ɉ�l�ɂ����f���ɔ��M�����z�u����Ă���Ƃ��܂��B
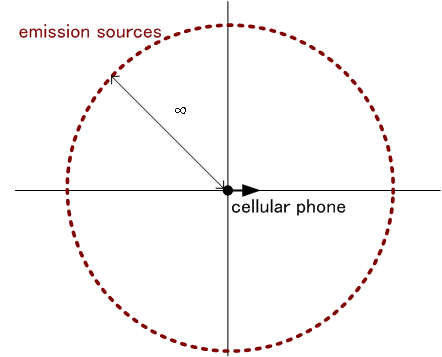
���_�ɋ���[���́A�E�֑��x 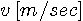 �ňړ����Ă��܂��B�@�e���M�������M������g���́A�h�b�v���[�V�t�g�̂��߂ɁA �ňړ����Ă��܂��B�@�e���M�������M������g���́A�h�b�v���[�V�t�g�̂��߂ɁA
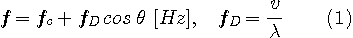
�̂悤�ɕω����܂��B�@�����ŁA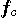 �͊�n�ǂ��甭�M���ꂽ�����g���g���A �͊�n�ǂ��甭�M���ꂽ�����g���g���A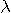 �͔����g�̔g����\���Ă��܂��B �͔����g�̔g����\���Ă��܂��B
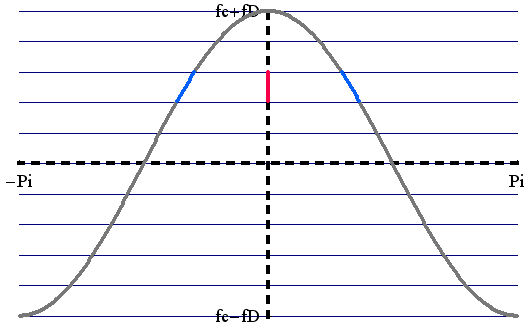
�c���̎��g���Ԋu�ɋ敪���܂��B�@�Ԃ��敪�Ɋ܂܂���M�g�̃p���[�͗]�����̐��������瓞���������̂ł��B�@��������
 �� �� 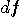 �Ƃ̊Ԃɂ� �Ƃ̊Ԃɂ�
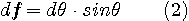
�̊W������A���������āA���i�P�j�Ǝ��i�Q�j����A
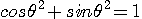 ��p���� ��p����  ����������� �����������
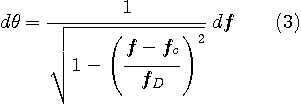
�������܂��B�@�~����̔��M���̑��p���[���P�Ƃ���ƁA [radian] �͎��g�� [radian] �͎��g��  �ł̓d�̓X�y�N�g����\���Ă���A���}�̂悤�ɂȂ�܂��B �ł̓d�̓X�y�N�g����\���Ă���A���}�̂悤�ɂȂ�܂��B
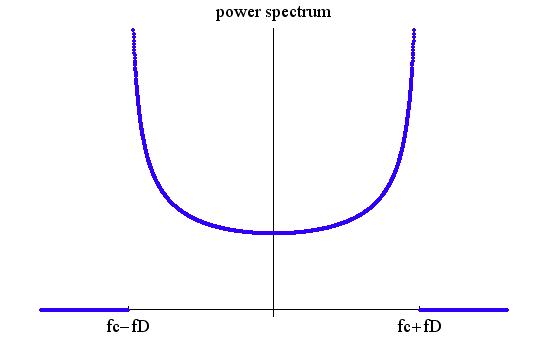
�ȏオ�]���̒��ۃ��f���ł����A���ۂ̌g�ѓd�b�̒ʐM�ł́A�p���X���ǂ悤�ɕό`���邩�H�@���邢�́A�ǂ̂悤�ȑ����ŕό`���邩�H�@���d�v�Ȗ��ƂȂ�܂��B�@��̂悤�ȃ��f�����ł͂��̖����������Ƃ��ł��܂���B�@���Ƃ����āA��ʓI�ȃ��f���͓�����ł��B�@����Ȃ킯�ŁA�ł��邾�������ɍ������V�~�����[�V�������f������邱�Ƃɂ��܂��傤�B�@�h�l�s�Q�O�O�O�̂v�[�b�c�l�`�̐��l��O��Ƃ��A
- �����g�� 2 GHz �i���������āA�g���������^2GHz = 15cm)
- �p���X�i�`�b�v�j���x�� 3.84M chips/sec.�i���������āA�p���X�Ԋu�������^3.84M
= 78m)
- �ړ����x�� 54 Km/hour = 15m/sec �i���������āA
 ) )
�Ƃ��Ă݂܂��B�@���̂Ƃ��A�g�ђ[���́A���̂悤�Ɏ�M���Ă��邱�ƂɂȂ�܂��B
- 15cm�i�����g�̔g���j�� 1/100 �b�ňړ����A���̊Ԃ� 38.4�`�̃p���X����M����B
- �ő�h�b�v���[�V�t�g�ł́A���f�p���X�̈ʑ��� 38.4�`�ň��]����B�@�s�X�ł́A�����̏ꍇ�A�ߋ����ŋ������˂��N���邽�߁A���f�p���X�����v��]�Ɣ����v��]���J��Ԃ��Ȃ����M���Ă���B
- �}���`�p�X�̍ő�o�H���� 150 ���[�g�����x�Ƃ���ƁA�T�O�����[���I�t���i�C�L�X�g�p���X�ŁA���������X�g�i�t�B���K�[�j���f���ŏ\���B
- �����̑傫�ȃr������A�������˂�����ꍇ���l������ƁA�X�g�ȏ�̈��S�v���K�v�B
- �߂��ɔ��˂��W�����Ă���P�[�X�A��������傫�Ȕ��˂�����P�[�X�A���ʂ����̃P�[�X�̂R�̃P�[�X�ɂ��āA�X�y�N�g���ω��͉��}�̂悤�Ȑ��������B
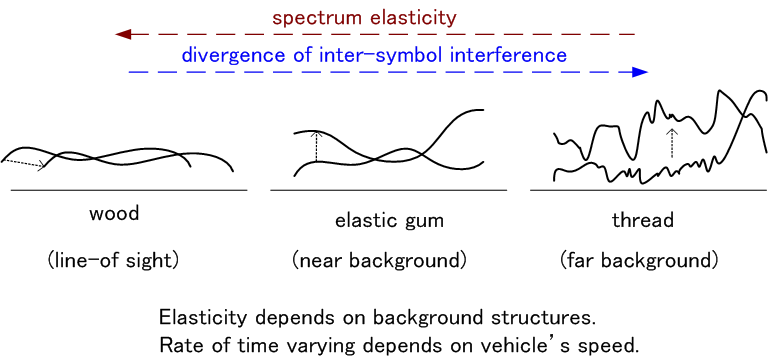
�b�c�l�`��M�ŏd�v�Ȃ��Ƃ́A���Ȃ��Ƃ��������i���Ƃ��A256�`�b�v�^�t���[���j���Ńp���X�g�`���s�ςł��邱�Ƃł��B�@�������A�K���q�`�j�d�Ȃǂ̃p�����[�^����i�����t�B���^�[�̐���j�ł́A�t���[�����ɔ����C������̂ŁA���Ȃ��Ƃ����t���[���ɓn���Ă��܂�ϓ����Ȃ����Ƃ��]�܂�܂��B�[�������ɑ����ړ�����ꍇ�́A�K���q�`�j�d���ʐM�s�ɂ܂�܂��B���̏ꍇ�̒ʐM�����ɂ��ẮA�ʼn������������ǂ݂��������B
��̓I�ɃV�~�����[�V�����Ŋm�F���Ă݂܂��傤�B�@�V�~�����[�V�������f�����ȉ��̂悤�ɉ��肵�܂��B
- ��n�ǂ���̐M���������̃|�[���ɂ���Ĕ��˂���B�@���˂ɂ���Ĉʑ��������_���ɕς�B�@�U���͓����Ƃ���B
- �|�[���ƈړ��[���̋�����
 ���[�^�[�̂Ƃ��A��M���x�� ���[�^�[�̂Ƃ��A��M���x�� 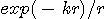 �Ƃ���B�@ �Ƃ���B�@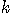 �͕����萔���猈�܂��r�I�����Ȑ����B �͕����萔���猈�܂��r�I�����Ȑ����B
- ���̃|�[���������ς��z�u���A�����M���Ƃ���B
- �ړ��̂𑖂点�āA�e�|�[������̐M���̑��a����M����B
- �����g�i
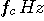 ) �œ������g���A�p���X�̕ω����ς�B ) �œ������g���A�p���X�̕ω����ς�B
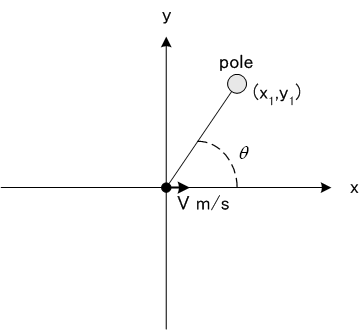
�܂��A��̂悤�ɁA���W 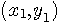 �Ɉ�̃|�[�����l���܂��B�@�ړ��[���͎����[���i �Ɉ�̃|�[�����l���܂��B�@�ړ��[���͎����[���i 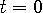 ) �Ō��_�ɂ���AX�����E�����֕b�� ) �Ō��_�ɂ���AX�����E�����֕b��  �ňړ�����ƁA���� t �b�Ŏ�|�[������̔��˔g�����g�������ʂ͈ȉ��̂悤�ɏ����܂��B�@ �ňړ�����ƁA���� t �b�Ŏ�|�[������̔��˔g�����g�������ʂ͈ȉ��̂悤�ɏ����܂��B�@
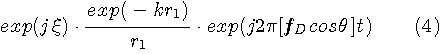
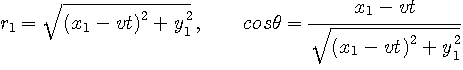
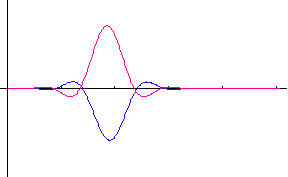
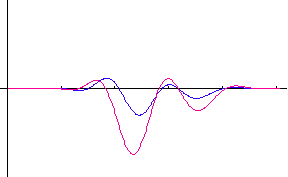
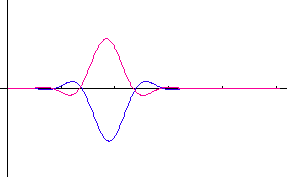
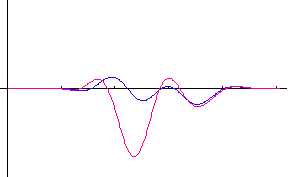
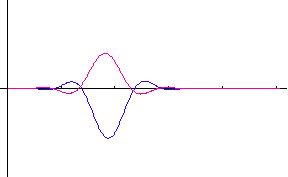
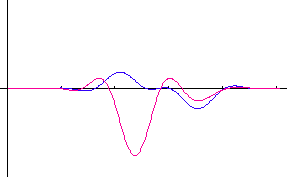
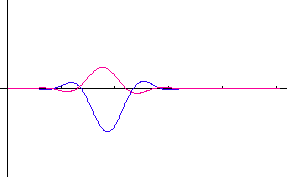
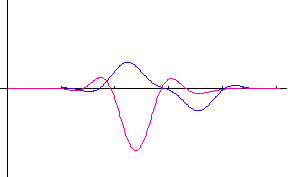
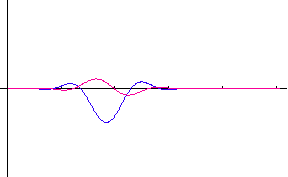
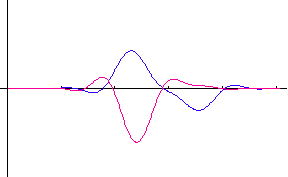
�����ŁA �͔��˂ɂ�郉���_���ʑ��ł��B�@���}�́A�R�Q�̃|�[���i�Ԃ��_�j�̂Q�̔z�u��ɑ��āA�p���X�̎��ԕω����V�~�����[�V�����������ʂł��B�@�|�[���z�u�}�̏c���Ɖ����̖ڐ���̓��[�g���ł���A�p���X�̔g�`�ω���
2048 chips ���ƂɎ����Ă��܂��B�@�͎����A�Ԃ͋����ł��B�@2048×5
chips �̊ԂɁA�ړ��[���͍��W���_����E�� 15m/sec �̑����� 4 cm
�����ړ����Ă��܂��B �͔��˂ɂ�郉���_���ʑ��ł��B�@���}�́A�R�Q�̃|�[���i�Ԃ��_�j�̂Q�̔z�u��ɑ��āA�p���X�̎��ԕω����V�~�����[�V�����������ʂł��B�@�|�[���z�u�}�̏c���Ɖ����̖ڐ���̓��[�g���ł���A�p���X�̔g�`�ω���
2048 chips ���ƂɎ����Ă��܂��B�@�͎����A�Ԃ͋����ł��B�@2048×5
chips �̊ԂɁA�ړ��[���͍��W���_����E�� 15m/sec �̑����� 4 cm
�����ړ����Ă��܂��B
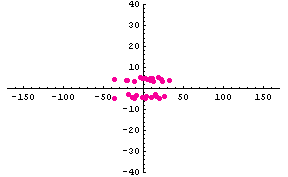
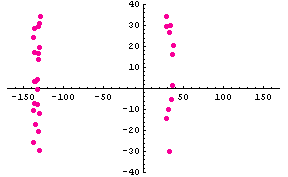
���F�@�[���̈ړ����x�ɍł������ǐ����ăV���{�����肷����@�̓u���C���h�n��ł��B�u���C���h������Q�Ƃ��Ă��������B���̃y�[�W����u���C���h�n��̉�����iPDF)�������N����Ă��܂��B
|


 ���m���ϐ��Ƃ���m���ߒ����l���邱�ƂɂȂ�B�@�[�����猩�āA�ǂ̕����̔��M�����m���I�ɋψ�Ƃ���B
���m���ϐ��Ƃ���m���ߒ����l���邱�ƂɂȂ�B�@�[�����猩�āA�ǂ̕����̔��M�����m���I�ɋψ�Ƃ���B
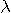 �͔����g�̔g����\���Ă��܂��B
�͔����g�̔g����\���Ă��܂��B
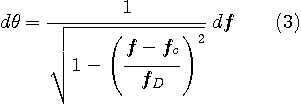


 ���[�^�[�̂Ƃ��A��M���x��
���[�^�[�̂Ƃ��A��M���x�� 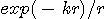 �Ƃ���B�@
�Ƃ���B�@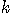 �͕����萔���猈�܂��r�I�����Ȑ����B
�͕����萔���猈�܂��r�I�����Ȑ����B