

|
固有値解析 (確率過程の場合:Karhunen-Loeve expansion) |
|
もっともポピュラーな確定的信号の直交展開としてフーリエ級数展開が挙げられます。 有限区間 [0, T] における信号をフーリエ級数展開した結果が次のようになったとします。
各周波数の係数の大きさ フーリエ級数展開と同様に、十分長い有限区間 [0, T] をとり、最小にすべき汎関数を次のように定義します。
ここで、
これらを使って、式(1)を展開していきます。
第1項は信号電力なので一定値であり、第2項を最大にすればよい。
を、制約条件
のもとで、最大化せよ。 この変分問題を解くと次が得られ(変分法を参照)、これを Karhunen - Loeve 展開と呼んでいます。 最適解は下の積分方程式の解である。
ここで
の両辺と
さらに、
なので、展開係数の間に次の無相関性が成立していることがいえます。
離散信号に対して数値計算する場合は、式(7)は行列の固有値と固有ベクトルを求める問題に帰着します。 なお、自己相関行列は対称(複素信号ではエルミート)なので、固有値は正で、N が大きいときは、電力スペクトルのサンプル値を近似します(自己相関行列を参照)。 現実の応用では、一応、エルゴード性を前提として集合平均を時間平均で代用します。 要するに、有限個のサンプル値で上のストーリーを近似することになります。 たとえば、
のような近似になるわけです。 時系列パターンの特徴抽出 (同じクラスの多数の見本パターンを固有空間に射影して典型パターンを決める作業) を例にとれば、見本パターンの個数は K に相当し、N<K で自己相関を求めるのが普通です。 もし、N>K ならば、自己相関行列のランクは K 以下になります。 N=64 とすれば、64×64 行列の固有値分解することになり、大きな固有値に相当する固有ベクトルを選んで、その部分空間で特徴抽出の作業を行うことになりす。 この程度なら、なんとか数値計算可能です。 しかし、画像では、ピクセル数=64×64=4096 ( =L ) 程度を扱うことになり、4096×4096 の共分散行列の固有値解析が必要になります。 これを避けるために K<<N とすると、ランクが K 以下の行列を扱うことになり、適当な K を選んで、 K 次元以下の固有空間にパターンを射影すれば済むはずです。 この方法を、”snapshots” と呼んでいます。 概略は次のようです。 まず、上の通常処理を整理すると次のようです。 画像の走査データ(長さ
L=N×N ) の K 個のパターンを並べた L 行 K 列のパターン行列
定理 |
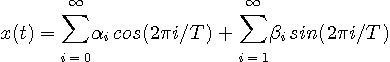
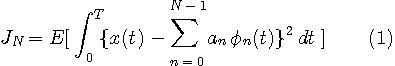
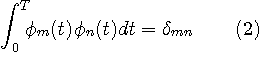
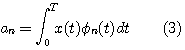
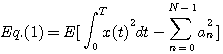
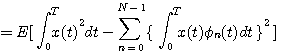
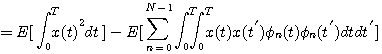
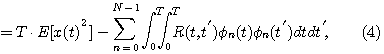
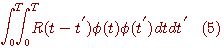
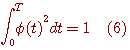
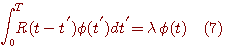
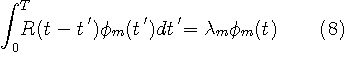
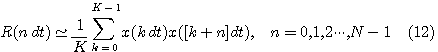
 とすると、
とすると、