

|
マルコフ情報源のエントロピー Entropy of Markov source |
|
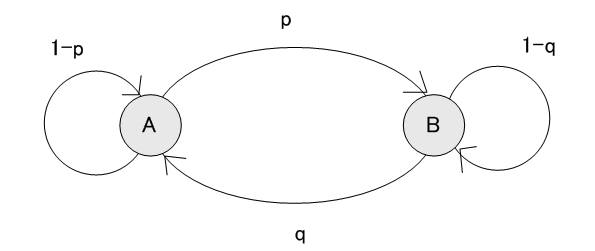
2つのアルファベット A と B を出力する単純マルコフ (Andrei Andreyevich Markov, 1856-1922) 情報源がもっとも簡単な例です。 まず、この例でエントロピーを計算してみましょう。 遷移図は下のように描くことができます。
A の次にまた A が出る確率=1-p A が出力されたことを知った後で、次のアルファベットを読むときに得る情報量の平均(条件付エントロピー)は
です。 同様に、B が出力されたことを知った後で、次のアルファベットの条件付エントロピーは
です。 これらのエントロピーをそれぞれ A と B の頻度で平均したものが求めるエントロピーになります。 A と B の頻度(定常確率)は、連立方程式
を解いて、
となるので、エントロピーは次のようになります。
次に、この定常確率でアルファベットが無記憶に出力されるような情報源を仮想してみましょう。 これを随伴情報源と呼んでいます。 随伴情報源はマルコフ性(規則性)を失っていますから、そのエントロピー
は元のマルコフ情報源に比べて大きいはずです。 すなわち、
がいえるはずです。 一般的な証明は省きますが、たとえば、遷移を対称
となり、
であることがわかります。
次に、上の話を一般化してみます。 長さ m のアルファベットの綴りはたくさんありますが、それらに番号
の情報を得ます。 したがって、
はブロック
このエントロピーはブロック長 m を大きくすればするほど、情報源のエントロピーを正確に近似することは明らかです。 上の式でエントロピーを計算するには、条件付き確率
から、
が成り立ちます。 これを上のエントロピー
が得られます。 右辺第1項は、マルコフ情報源から出力される文章を、長さ m+1
の綴りを独立に出力しているとみなした (m+1)次拡大随伴情報源のエントロピーを意味しており、単位は
ビット/(m+1)文字 です。 同様に、第2項はm次随伴情報源のエントロピーであり、単位は
ビット/m文字 です。ブロックの定常確率は、ブロック間の遷移確率
の解です。
が得られます。 これは、シャノンが英文のエントロピーを計算する論文で導いた結果です。 すなわち、長さ m+1 の綴りの頻度表と長さ m の綴りの頻度表があれば、それらの綴りが独立に生起するとした随伴情報源のエントロピーの差でマルコフ情報源のm次近似が計算できることを表しています。 さらに、この近似は単調に真のエントロピーに近似するはずですから、
が成立します。 実際の統計データは、綴りの頻度(上の連立方程式の解 |
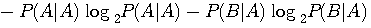
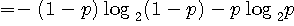
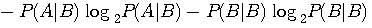
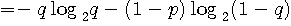
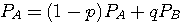
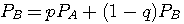
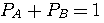
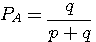
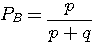
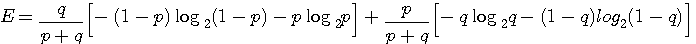
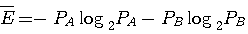
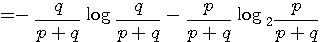

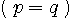 とすると、それぞれのエントロピーは
とすると、それぞれのエントロピーは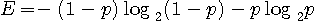
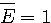

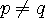 のときの
のときの  と
と  の曲面を下に示します。 一番上の図は
の曲面を下に示します。 一番上の図は  を、2番目は
を、2番目は  を、3番目は二つを重ねて描いたものです。
を、3番目は二つを重ねて描いたものです。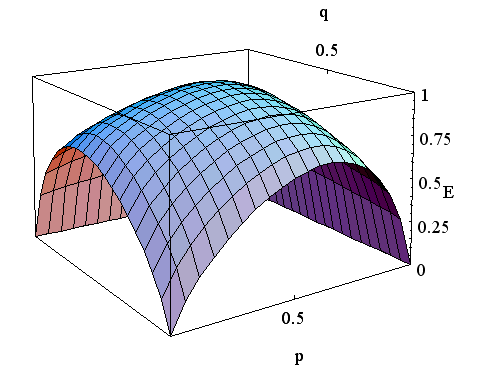
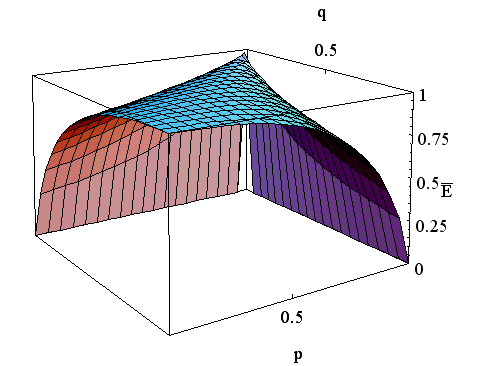
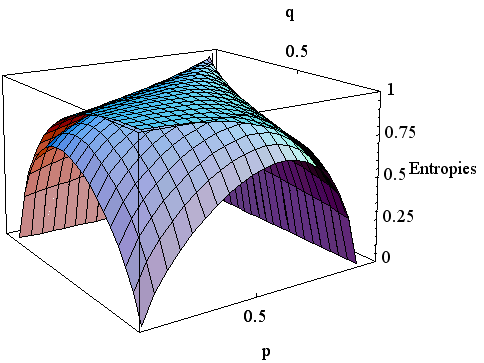
 をつけて、
をつけて、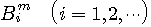 で表し、これをm次ブロックと呼ぶことにします。 m次ブロックの総数は、アルファベットの種類の数を
で表し、これをm次ブロックと呼ぶことにします。 m次ブロックの総数は、アルファベットの種類の数を
 とすると、
とすると、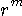 個になります。 文章中のアルファベットの出現は、条件付き確率
個になります。 文章中のアルファベットの出現は、条件付き確率 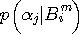 に支配されますが、その精度はブロック長 m が長ければ長いほど高くなります。 もし、対象とする情報源が
n(
に支配されますが、その精度はブロック長 m が長ければ長いほど高くなります。 もし、対象とする情報源が
n( ) 重マルコフ情報源 ならば、n より大きい任意の m に対して
) 重マルコフ情報源 ならば、n より大きい任意の m に対して 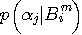 は同じ値を与えるはずです。 実際の場面では、対象とするマルコフ情報源が何重なのか、予めわからないケースが多いのですが、m
を十分大きく選んで
は同じ値を与えるはずです。 実際の場面では、対象とするマルコフ情報源が何重なのか、予めわからないケースが多いのですが、m
を十分大きく選んで
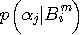 を与えれば、マルコフ情報源を完全に記述できます。 m次ブロックを読んだとき、その知識をもったうえで、次に続くアルファベットを読むと、我々は
を与えれば、マルコフ情報源を完全に記述できます。 m次ブロックを読んだとき、その知識をもったうえで、次に続くアルファベットを読むと、我々は
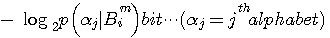
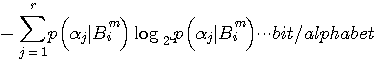
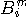 の次に一つのアルファベットを読んだとき、平均として得る情報量を表しています。 さらに、この平均情報量をブロックで平均すれば、次のようにエントロピーが計算されます。
の次に一つのアルファベットを読んだとき、平均として得る情報量を表しています。 さらに、この平均情報量をブロックで平均すれば、次のようにエントロピーが計算されます。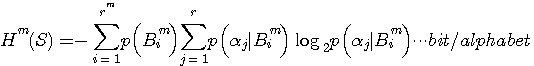
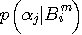 が必要です。 しかし、多くの場合、条件付き確率よりも同時確率
が必要です。 しかし、多くの場合、条件付き確率よりも同時確率 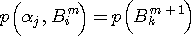 で統計データが与えられます。 上式をこの同時確率で表現してみます。 まず、ベイズの公式
で統計データが与えられます。 上式をこの同時確率で表現してみます。 まず、ベイズの公式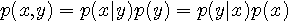
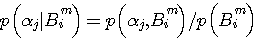
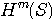 を与える式に代入し、
を与える式に代入し、 が (m+1)次ブロックであることに注意して、
が (m+1)次ブロックであることに注意して、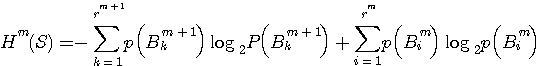
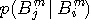 を要素とする係数行列をもつ連立一次方程式
を要素とする係数行列をもつ連立一次方程式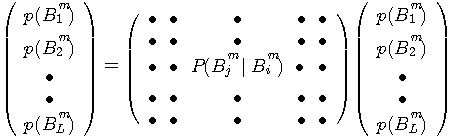
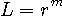
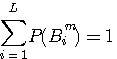
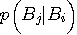 の意味については
の意味については で表すと、上の結果から、
で表すと、上の結果から、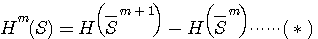

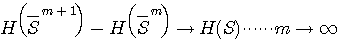
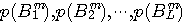 )ですから、上の連立方程式を解く必要はなく、簡単に式(*)でm次近似エントロピーを計算することができます。 m
を増やしながら収束の具合をみて、適当なところで計算を終了します。
)ですから、上の連立方程式を解く必要はなく、簡単に式(*)でm次近似エントロピーを計算することができます。 m
を増やしながら収束の具合をみて、適当なところで計算を終了します。