

|
相関符号伝送 (整数係数の場合) Correlative code transmission |
|
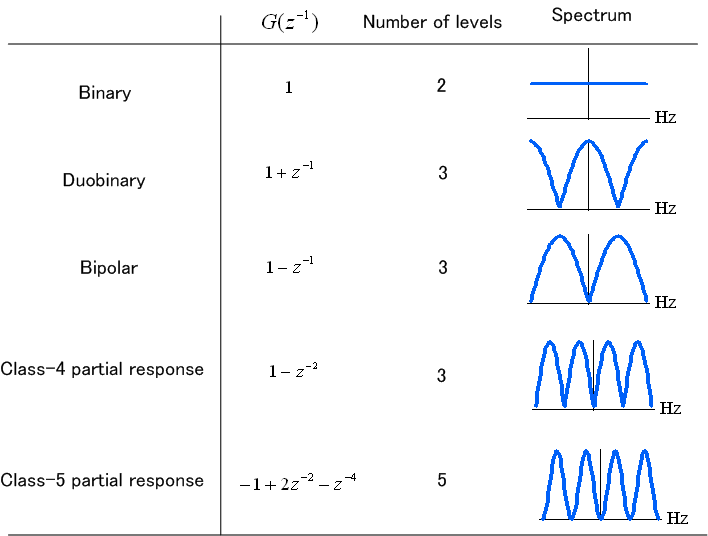
いわゆる、デュオバイナリ (Duobinary) 、バイポーラ (Bipolar)
と呼ばれる一連の送信符号化技術を指します。 目的は、送信信号のスペクトルを成型することであり、たとえば、磁気記録のように直流成分を通さない媒体に対して、予め直流成分を持たない信号を用いてパルス歪みを避けるなど、さまざまです。 一般形は、たとえば2値データ
のような整数係数をもつ線形ディジタルフィルターです。 これを遅延オペレーター
のように書けます。 係数が整数なので、送信シンボルは
の範囲の整数値(必ずしもすべてではない)をとるので多値伝送となります。 特に、
のようなものを、General partial response と呼んでおり、Duobinary も Bipolar もこれに属します。 相関符号を行うと、レベル数が増加し、それを単に判定すると誤り率が劣化します。 この劣化は最尤系列推定 ( ビタビ・アルゴリズム )によって克服できます。
注1:単に「相関符号伝送」と言えば、符号と復号の回路が簡単な、整数係数の場合を指しているようです。係数を有理数に一般化することも可能です。この場合の興味深い伝送方式として、 THP ( Tomlinson Harashima Precoder ) があります。 これは、加法的白色ガウス雑音の条件下で伝送路の周波数特性が分かっているとき、伝送路応答を相関器(係数は整数ではない)と見做し、そのプリコーダーを送信側に置くという発想です。この方法は、送信情報を最小の損失で送る意味から、最適な伝送方式です。
<プリコーダー>
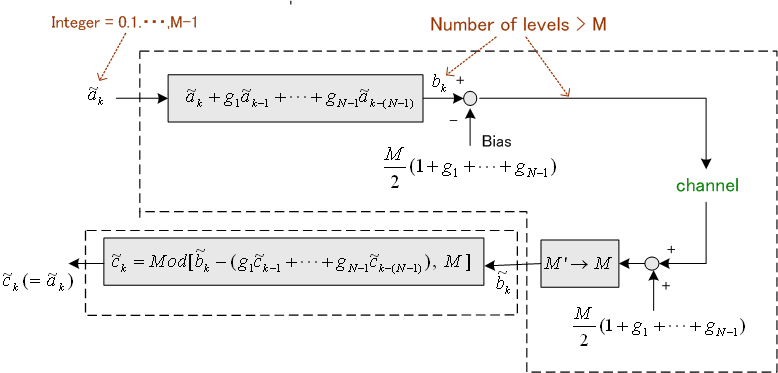
説明の簡単のため、バイポーラについて話を進めます。 バイポーラは直流とクロック周波数にスペクトル・ヌルをもっているので、直流を通さない伝送媒体に対して有利であり、かつ、シンボルクロックのパイロット・トーンをヌル周波数の位置に挿入することができます。 とりあえず、ストレートにブロック図を描くと下図のようになります。
問題なのは、受信側で相関をほぐすディジタルフィルタ
このシステムも、いったん判定誤りが発生すると誤りが永遠に伝播してしまうのでダメです。 このような問題を解決する手段がプリコードです。 一般的にいえば、次のような仕組みです。 冒頭の式(1)の送信データを非負の整数と仮定します。 もし、M値データならば、
要するに、伝送系は点線で囲んだ二つの部分に分割され、それらは互いにMを法として(Modulo
Mで)演算されるフィルターとその逆フィルターの関係になっています。 すなわち、
を直列に接続したものです。 これらの順序は交換可能ですから、式(6)を送信側に移すと、バイポーラーのプリコーダーモデルが次のように得られます。 式(6)の帰還ループを送信側に移すことにより、受信側での誤り伝播の心配が無くなりました。 なお、受信側で、3値判定を用いれば送信データの絶対極性を判定可能ですが、Modulo 2 をとると差動符号(極性反転に情報を乗せるシステム)になります。
<誤り検出/再送>
バイポーラーの特徴は、
まず、ある瞬間に限定してシンボル判定に着目すると、2値伝送のシンボル間隔は
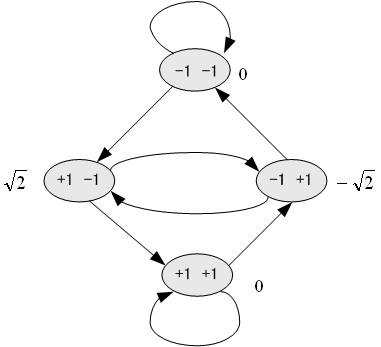
上のカーブには大きな差がありますが、これはバイポーラーの特徴を利用していないことに起因しています。 バイポーラーの最大の特徴は、 <最尤系列推定>
に対する最短信号間距離の信号は、 (1) 連続する
(2)
(3) 連続する
などです。 この信号間距離は2値伝送の最小信号間距離(一箇所だけ、 注2: 最尤系列推定を実行する有限記憶容量のビタビ・アルゴリズムの装置化においては、アルゴリズム固有の誤り増幅があり、別途この評価が必要です。 注3: ここで述べた内容は、送信スペクトルを簡単な回路で成形する手法でした。加法的白色ガウス雑音の条件下で、伝送路の周波数特性が分かっているとき、送信情報をもっとも効率良く送る手法として、 THP ( Tomlinson Harashima Precoder ) があります。これは、伝送路応答を相関器(係数は整数ではない)と見做し、そのプリコーダーを送信側に置くという発想です。 |
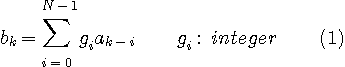
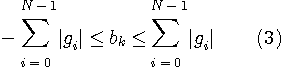
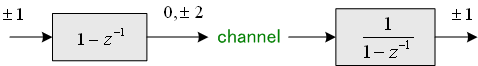

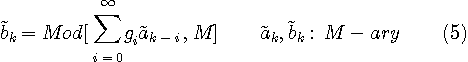
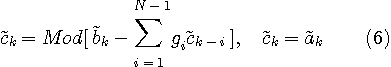
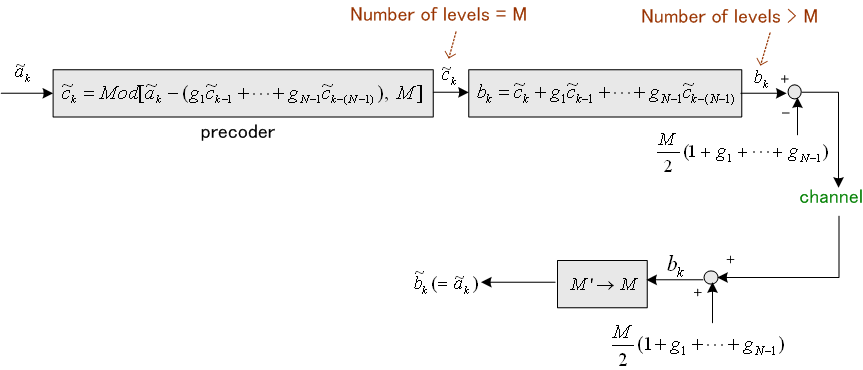
 であるのに対して、バイポーラーのシンボル間隔は(3値判定するので)
であるのに対して、バイポーラーのシンボル間隔は(3値判定するので) 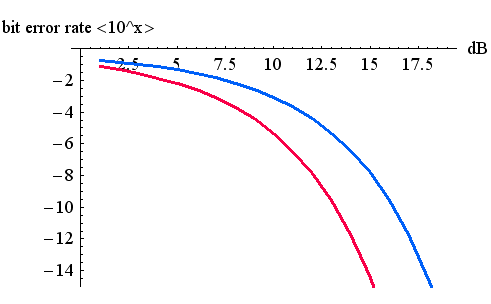
 の区間の二つの
の区間の二つの  と
と  が異なる)に等しく、最尤系列推定の誤り率は3dB劣化を回復し、2値伝送と同等になることがいえます。
が異なる)に等しく、最尤系列推定の誤り率は3dB劣化を回復し、2値伝送と同等になることがいえます。