|
ミニマックス等化の解 Solution of minimax equaliztion (zero-forcing principle) |
|
送信シンボルの可能なすべての系列について符号間干渉の絶対値
で与えられ、さらに基準化した形は
のように表せます。 ここで、
ＱＡＭなどの複素信号についても、同様に
が得られます。 これは、符号間干渉の最大半径を表しています。このような評価関数をピーク歪と呼んでいます。
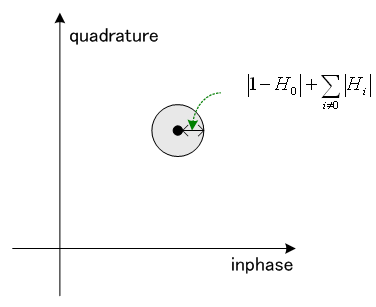
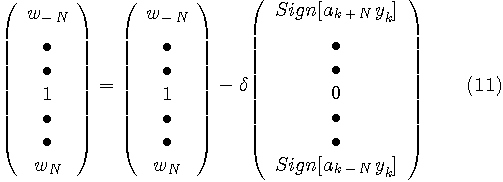
１９６６年、未だディジタル回路で通信装置を作る技術が無い時代、R.W.Lucky はミニマックス等化に関して次のような定理を導きました。 定理 チャンネル応答が、 すなわち、等化器から出力されるパルスに対して、そのピークを中心に前後Ｎ個のサンプル値を強引にゼロにすれば、ミニマックスの意味で等化が実現することを意味しています。 この操作から、「Zero-forcing 等化」 と呼ばれるようになりました。 Zero-forcing の古い特許には、この概念を下のように図解しています。 長〜い風船を両手で握ったとき、中央のボリュームが大きくなって、両側にはみ出したボリュームが小さくなる条件は？ といった感じです。
この定理は次のように一般化することができます。 下の定理で、 定理 条件（６）が成り立っていれば、任意の参照パルス
Zero-forcing はちょっと不思議な定理なので、以下に証明を付けておきます。 この結果は複素信号にも適用できます。 （証明）
において、Ｌ番目のタップ重み
ここで、
となります。 したがって、条件（６）のもとで、 R.W.Lucky の場合では、上の証明の中で、タップ重み
しかし、十分条件（６）が厳しいこともあり、またディジタル信号処理による最小自乗平均等化が可能になり、次第に Zero-forcing 等化は使われなくなりまた。 R.W.Lucky は、上のような証明を行って、ステップ修正の収束条件として十分条件（６）を設けましたが、ミニマックス最適化の十分条件としては狭すぎるのではないか？ という疑問が湧きます。 本来、アルゴリズムの収束と Zero-forcing 等化が可能な十分条件とは直接的関係は無いはずです。 以下、このことについて簡単な例題で検討してみましょう。 R.W.Lucky の定理に戻って、もう少し詳細に性質を調べます。 逆システムで解説したように、一般的な（非最小位相推移の）応答は、因果的であって因果的逆をもつ応答と反因果的であって反因果的逆をもつ応答のコンボリューションで表現されました。 この最も簡単な例題に対してミニマックス等化を検討してみましょう。 一般論は大変難しく、未だ解かれていません。 例題のチャンネル特性を、
とします。 この応答は {
となり、右辺の左側の分数が安定な反因果的逆、右側が安定な因果的逆です。 この展開は、
ですが、応答 {
のような zero-focing を実行してしまいます。 でも、十分条件（６）が満たされていないので、果たしてミニマックスの意味で等化されるかどうかが不明です。 更に、この時間原点でタップ数を無限に多くしたときを想像すると、因果的逆、
を一生懸命求めることになり、発散します。 このようなケースに十分条件（６）を当てはめることには無理がありそうですね。 やはり、値は小さくても、真ん中の
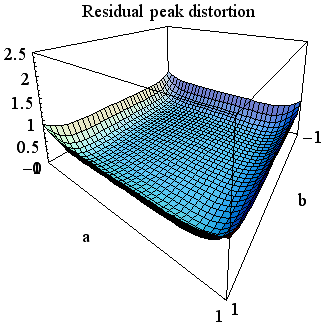
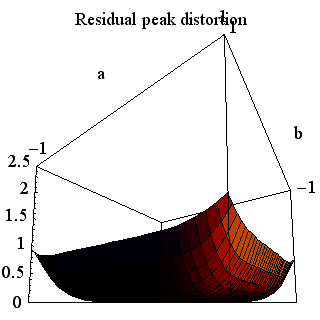
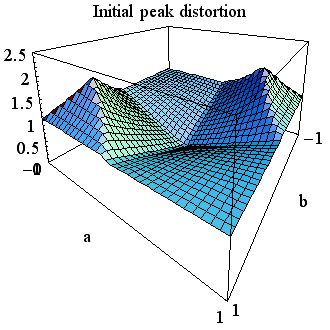
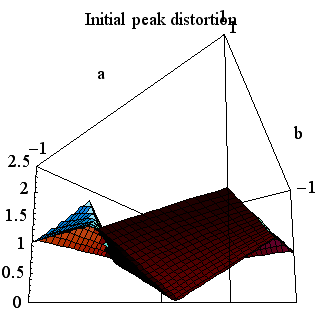
のように与えられます。 この曲面は下図のようになります。 左は高い角度から眺めたもの、右は底辺から眺めたものです。 中央で、曲面は底辺（ピーク歪＝０）に接しています。 もし、時間原点を { そして、 上の３通りの図を比較すると、 時間原点を 上の疑問について確かめなければなりません。 もし、十分条件（６）が満たされていれば、誤差
に対して、
となるように では、 期待される答えは、「たとえ十分条件（６）を満たさなくても、 となってしまい何も等化しない状態になって意味がありません。 次に、<1> と <2> を同時に zero-forcing すると となり、これも意味がありません。 <4> と <5> についても同じことが言えます。 ミニマックスを実現し得るケースとして、次の３つが残りました。 <1>, <3>, <4> <2>, <3>, <4> <2>, <3>, <5> 左と右は、とびとびに zero-forcing しています。 このような可能性はあるでしょうか？ 式で確認すれば無いことが分かりますが、数値計算して視覚的に見ることにしましょう。 <2>, <3>, <4> の組の曲面は上で示しました。 左と右は対称な関係にあるので同じ結果をもたらします。 たとえば左を選んで、等化後ピーク歪を数値計算すると下のようになります。 この差異をみるために、 <2>,<3>,<4> の曲面 ー <1>,<3>,<4> の曲面 をプロットしてみると下のようになり、期待通り、<2>,<3>,<4> が常にミニマックスを与えていることが分かります。 ちなみに、時間原点を
注： このページの内容は、典型的かつ簡単な例題による zero-forcing の検討であり、zero-forcing 等化の一般論は未だ十分に研究されていないようです。 |
の最大を評価し、これを最小にする等化をミニマックス (MiniMax ) 等化あるいはそのアルゴリズムの原理からゼロフォーシング
( Zero-forcing ) 等化と呼んでいます。 多値シンボルの最大レベルを仮に±１とすると、最悪符号間干渉は
はチャネルと等化器からなるトータルシステムの応答を表します。
を調整すれば 
が最小になる。
, 
とした場合が R W Lucky の定理です。
について
を調整すれば
が 
だけ変化したとします。 すると、式（９）は
としても一般性を失わないので、
を 
と逆符号に選べば
を 
と逆符号で適当に小さくとれば、
を減少することができます。 そして、Ｌは任意だったので 
を満たす 
は一意であり、これが 
を最小にする解になります。（証明終わり）
の変化 
を 
と逆符号に選ぶことになります。 したがって、等化出力のパルスを見て、
の極性と逆方向に 
を 単位ステップ 
だけ修正する単純な操作をすべての L について行い、これを繰り返せばミニマックスの解へ収束することがいえます。 このことが、タップ重みを抵抗回路網で実現していたアナログ時代に大変有効だったわけです。 たとえば、中央タップを１に固定した次のようなアルゴリズムがアナログ回路で実現できました。 この等化によって、基準化されたピーク歪
が最小化されます。
} で、中央の 
が時間原点です。 この逆システムは
を時間原点に選び、ここでピーク（＝１）をもつように等化することを意味しています。 しかし、式（１２）を展開すると、
} の中で一番大きな絶対値をもつ項は、
, (
) を変化させると移動します。 たとえば、
とすると、応答は { 
} となり、最初の項 
がピークです。 Zero-forcing を単純に理解した人は、この時刻を時間原点とみて、
を時間原点にすべきではないかと思われます。 以下、３タップのケースで、時間原点を真ん中にとるべきことを確認しましょう。 初期ピーク歪は、
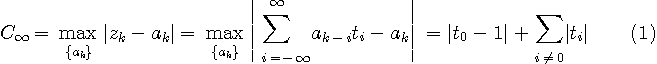
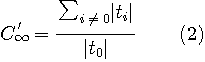
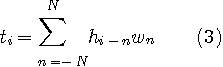
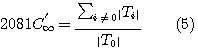
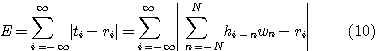
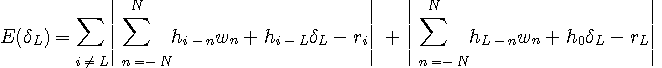
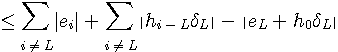
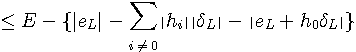
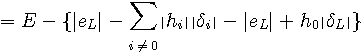
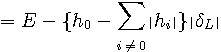
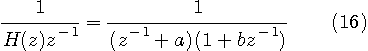
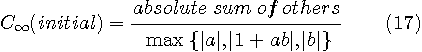
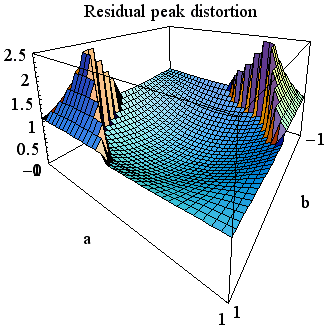
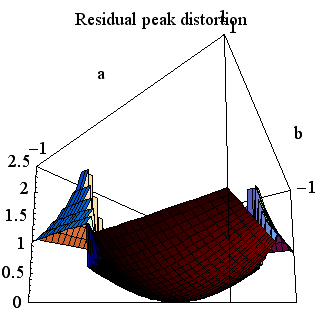
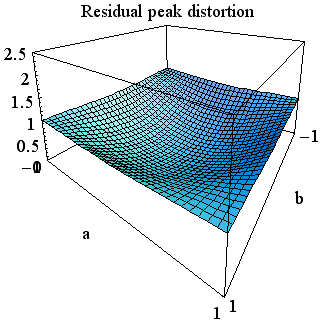
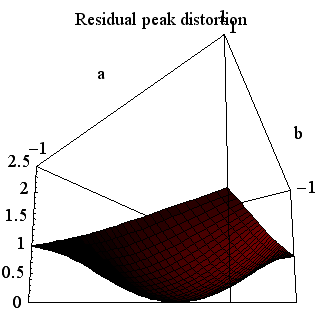
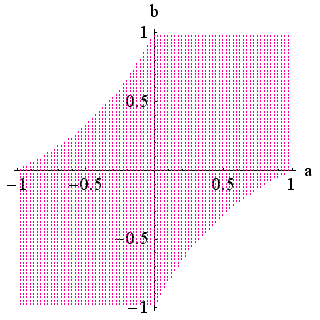
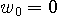
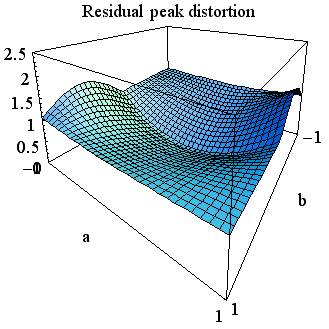
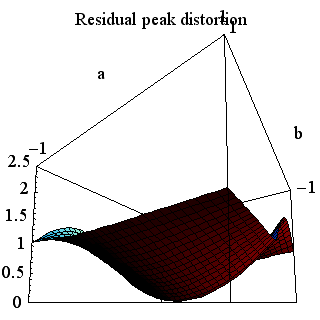
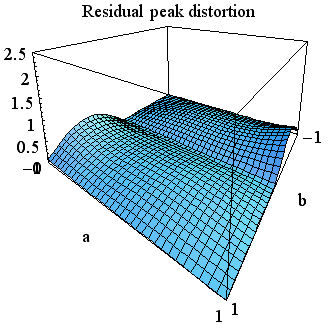
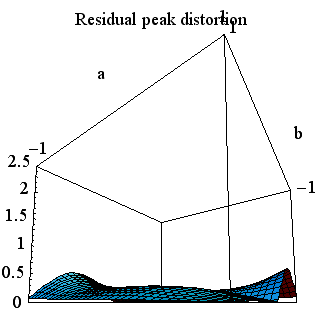
} の最大絶対値の位置に自動的に選んで zero-forcing すると、等化後のピーク歪は下図のようになります。 左は高い視点、右は低い視点で見た図です。 やはり、中央で底辺に接しています。
の位置に時間原点を固定すると下図のようです。 やはり、左は高い視点、右は低い視点です。 中央は底辺に接しています。
に時間原点を固定した場合の曲面が、全領域にわたって一番下にくることが分かります。 でも、未だ次の疑問が残っています。
に固定する正当性はありそう・・・。
を設定すれば、
が最小になることは定理から言えています。 そして、十分条件（６）が満たされる範囲は下図のようになっています。
の位置を時間原点として zero-forcing すればよい」ということですが、ここで
zero-forcing の幾何学的意味を考察する必要が出てきました。 ５個の方程式の集まり（１５）の左辺の絶対値の総和を最小にしたいわけですが、この解は必ずどれか３つの式をゼロにする解になっています。 直感的に言うと、一次式の絶対値は平面（３次元以上では想像できないですが、平面という概念は高次元になっても共通です）を、底辺をよぎる直線に沿って折り曲げた形をしています。 そのような折り曲げられた多くの平面図形の総和を想像してみると、その曲面はダイヤモンドカットのように平面を組み合わせた形をしています。 したがって唯一の最小解があるとすれば、それはダイヤモンドカットの一番下の角（かど）になっているはずです。 そして、その角（かど）は変数の個数に等しい方程式をゼロにしているはずです。 このように考えると、式（１５）の絶対値和を最小にする解は、５個の式から３つを選んで、それらを同時にゼロにする解をチェックすればいいことが分かります。 では、この考えを５個の式に当てはめてみましょう。 まず、真ん中の式
<3> は必ず含めなければなりません。 残る二つをどのように選ぶかが問題となります。 ５個の式のなかで、<1>
と <5> の式は特別な形をしています。 仮に、<1> と <5>
を同時にゼロにすると,
,, 
, 
に固定して、１５タップで zero-forcing した場合の残留ピーク歪は下図のようになります。
