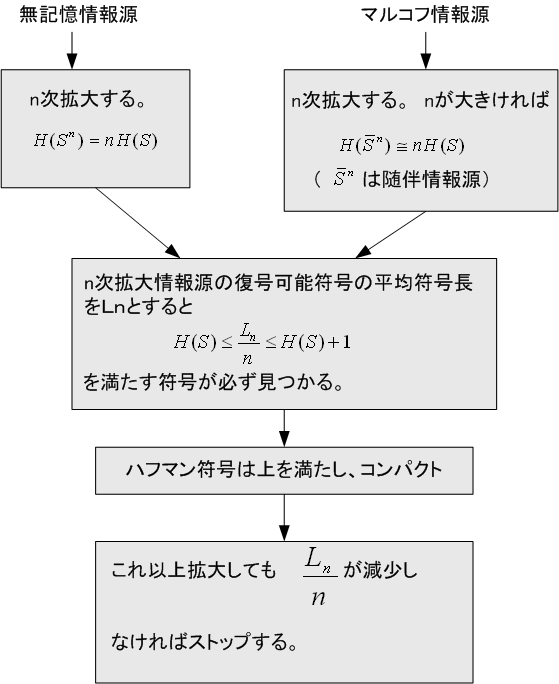
無記憶情報源（アルファベットを独立に出力する情報源）については、ハフマン符号が最良です。　最良の意味は、復号可能な（可逆な）符号の中で、１アルファベットあたりの平均符号長が最小ということです。このような符号化をコンパクトと呼んでいます。　ハフマン符号を用いて、限りなく情報源のエントロピー（情報源が１アルファベット当たり出力する情報量の平均）に近い符号を設計する方針は次のようです。

1. アルファベットをｎ 文字づつ区切り、元の無記憶情報源をｎ文字の単語を出力する情報源（ｎ次拡大情報源）とみなす。
2. この情報源について、ハフマン符号を設計する。
3. この符号の平均符号長（１単語当たりの符号長の平均）を計算しｎで割る。　これが情報源のエントロピーをまだ十分近似していなければ、n=n+1 として１へ戻る。

以上は、無記憶情報源の場合ですが、現実の情報源はマルコフ情報源です。　しかし、符号の設計方針は上とまったく同じでもかまいません。　直感的にいえば、情報源を拡大することによって、長いアルファベット列を単位として扱うことになり、そのアルファベット列の間の確率的依存性が薄れてゆくという事実に基づいています（英文の情報量を参照）。　ただし、拡大を大きくすると、アルファベット列の数は爆発的に増加し、演算量が増大します。　音声や画像のディジタル信号の圧縮では、可逆符号化の前に非可逆符号化を行います。これは、人間の聴覚や視覚で、認識が苦手な要素をどんどん省いてしまうという方法です。省いてしまった要素を元に戻すことはできません。この非可逆符号化の結果に対して、演算量が許容できれば、ハフマン符号を適用します。
以上の理論的な流れを描くと下図のようです。　極めて具体的な復号可能ということが、極めて抽象的な確率によって定義されたエントロピーと深い関係にあります。

注：　ハフマン符号の平均符号長は n によって単調減少するとは限らない。　多くの場合、n が小さいとき急減少するが、n が大きくなると（極限に近づくと）増減を繰り返す。