平均情報量（エントロピー）は、その情報源がどれだけ情報を出しているかを測る尺度です。　物理学でも、頻繁にエントロピーという言葉が出現しますが、その意味は 「乱雑さ」 「不規則さ」 「曖昧さ」 などといった概念を指します。　情報理論の場合もまったく同じ概念を指し、その情報が不規則であればあるほど、平均として多くの情報を運んでいることを意味します。

二つのアルファベット Ａ 、 Ｂ がランダムに出力されているとします。　こように、アルファベットが過去に依存しないで、独立に出力される情報源を無記憶情報源と呼んでいます。　それぞれの確率を 、 とします。Ａ が出力されたことを知ったぼくは ビットの情報を得ます。Ｂ ならば ビットです。　ぼくは、この２通りの情報量をそれぞれ確率 と で得ますから、平均として１アルファベット当たり、

の情報を得ることになります。　これが２種類のアルファベットの場合の平均情報量（エントロピー）です。　 、 として、この結果をプロットすると下のようになります。　

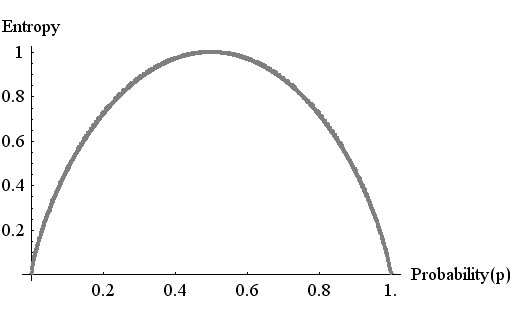
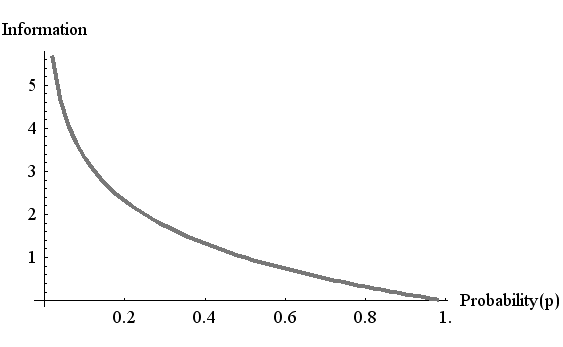
この図は、アルファベットの出現頻度に偏りがあるとエントロピーが小さくなることを表しています。　たとえば、「ハイ」ばっかり言う人は、平均として情報をあまり表現していないことを主張しています。　でも、このような人に、たまに「イイエ」と言われると、われわれはかなり驚きますね。　このとき、われわれは、下図の情報量のカーブからも分かるように、ものすごく大きい情報を知らされるわけです。　でも、普段は「ハイ」ばかりですから平均すると、この人が発する情報量は平均として小さいと言えるのです。　これは、情報量が対数関数で定義されたことに由来しており、統計的に情報を扱う範囲では、妥当なことなのです。

念のため、３つのアルファべット Ａ 、Ｂ 、Ｃ をランダムに出力する場合はどうでしょうか？　それぞれの発生確率を 、 、 とします。　このときのエントロピーは

で与えられます。　ここで、アルファベットの発生確率の総和は１なので、

この関係から を消去すると、次のようになります。

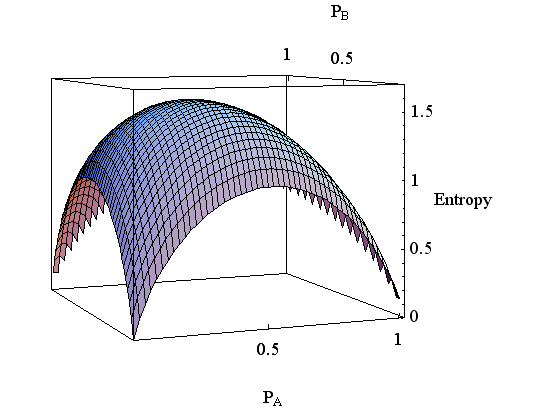
下の図は、２つの水平軸を 、 とし、エントロピー（Ｅ）の曲面を描いたものです。　 で最大値をとっています。

アルファベットが３以上の場合も同様に、次の定理が成り立ちます。

定理　
すべてのアルファベットを同じ確率で出力しているとき、
エントロピーは最大となる。

無記憶情報源から出力されたアルファべットを一定の長さ n ごとに切り、それを単語とみなします。　すると、この情報源は単語を単位として出力しているとみなせます。　このような情報源の解釈を ｎ次拡大といいます。　たとえば、A 、B 、C の３種類のアルファベットを出力する情報源の３次拡大は、２７種類の単語

AAA　AAB　AAC　ABA　ABB　ABC　ACA　ACB　ACC　・・・・・・・

を出力する情報源です。　これらの単語の出現確率は各文字の発生確率の積ですから、たとえば単語 AAC の出現確率は

で計算されます。　すべての単語についてこの計算を行い、エントロピー

を求めることができます。　すると、

が成り立ちます。　一般に次の定理が成り立ちます。　

定理
無記憶情報源のｎ次拡大のエントロピーは、
元の情報源のエントロピーのｎ倍に等しい。

実は、この定理はマルコフ情報源についても、ｎ が十分大きいとき成り立ちます。　このことが、無記憶情報源について体系化した情報圧縮などの原理がそのままマルコフ情報源に適用できる根拠になっており、実用上極めて重要な定理です。

シャノンは、英文のエントロピーを、
単語（平均長＝４．５文字）を出力する無記憶情報源と見做して計算しています。
大変興味深いので、是非、英文のエントロピーを参照してください。