|
トランスバーサル・フィルター Transversal filter |
|
線形システムはそのインパルス応答
トランスバーサルフィルター(transversal
filter )は、まだディジタル信号処理が出来なかった時代に、フィルターをアナログ遅延線を用いて実現しようとしたものです。 時間きざみを
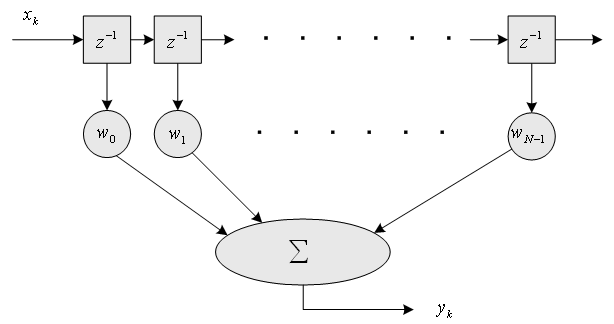
のようになります。 この総和を有限個で打ち切ったものを下に図示します。 ディジタル通信で用いられる自動等化器のほとんどはこの構造で、
遅延
のように書けます。 これは
このアナログモデルで、出力
ですが、
ここで、
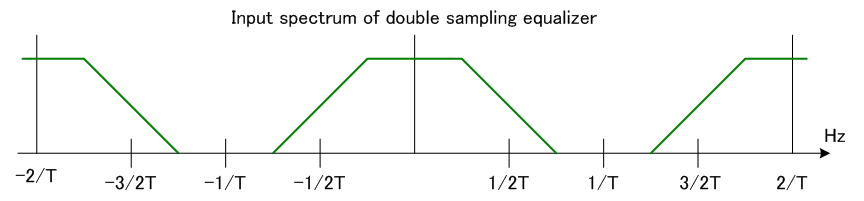
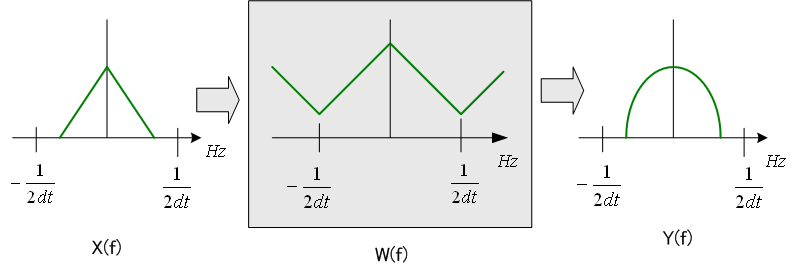
ディジタル通信で広く用いられる等化器として、ダブルサンプリング等化器があります。 これは送信シンボルの周期
に選んだものです。 一般に、送信パルスのロールオフは100%以下ですから、標本化定理を満たしています。 出力
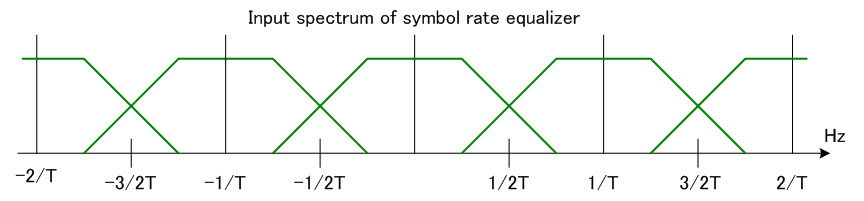
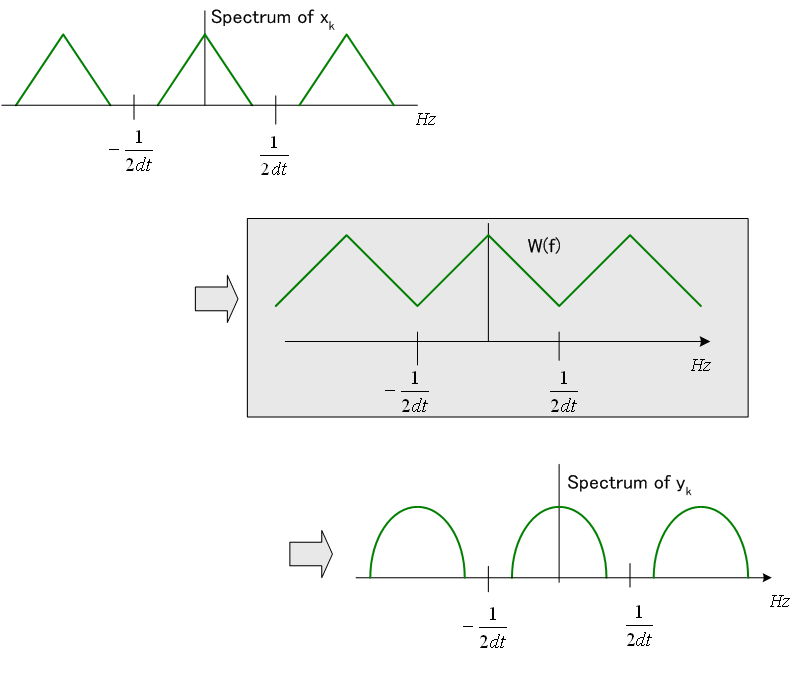
シンボルレート等化器では、
とします。 このとき、入力
シンボルレート等化器では、このようにスペクトルが重なった状態で信号が入力されます。 上は概念図なので位相特性を描いていませんが、信号がチャンネル歪を受けると大きな位相歪を受けて、重なりの部分はどんな形になるかわかりません。 もしかしたら、重なり部分でスペクトルヌルが発生するかもしれません。 もしスペクトルヌルが発生すれば、等化器はそれをカバーするために無限大の特性を実現しようとし、等化性能が劣化します。 |
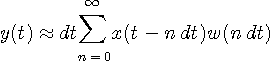
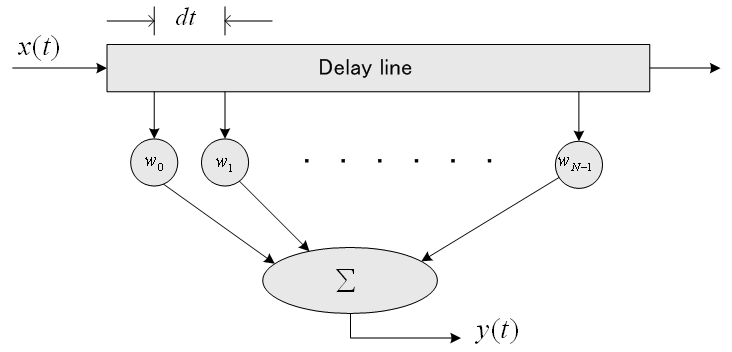
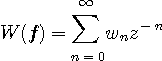
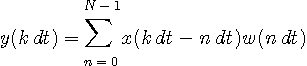
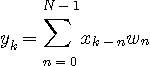
 の半分でサンプリングします。 上の構造で、
の半分でサンプリングします。 上の構造で、