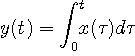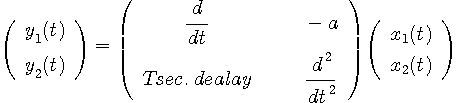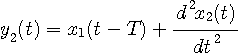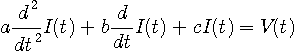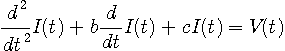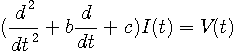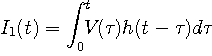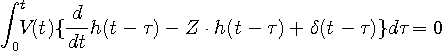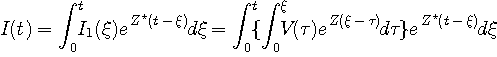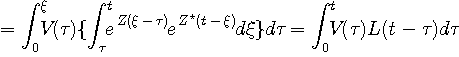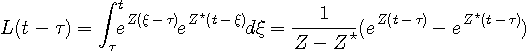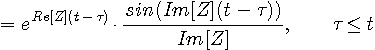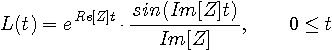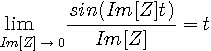を入力したときの出力を 、 を入力したときの出力を とします。
二つの入力信号の和 を入力したときの出力が
それぞれの出力の和 になっているとき、
このシステムを線形といいます。

以下は典型的な線形操作の例です。

１．　定数倍　　　　　
２．　遅延　　　　　　　
３．　微分　　　　　　　
４．　積分　　　　　　　
５．　Convolution
　　　　　

線形操作の間には次の関係が成り立っています。

１．線形操作（異なってもよい）を有限回多重操作したものも線形
　　　　　

２．線形操作（異なってもよい）の結果を加算しても線形
　　　　　

３．もし、逆操作が可能ならば、それは線形
　　　　　

４．したがって、逆操作が存在すれば、陰形式も線形
　　　　　
　　　　　

上のことは多次元へも拡張できます。　たとえば、

 y(t)=A・x(t)

 x(t), y(t) はベクトル、A は線形操作を要素とする任意の行列

 （ 例 ）

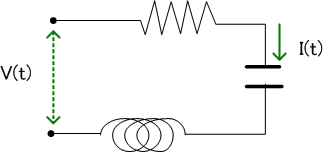
大学の電気回路実験に必ず登場するインピーダンスの測定では、下のような回路で、正弦波電圧信号 V(t) を与え、電流 I (t) を測りましたね。　そして、この回路がもっとも共振する周波数を実験で確認したと思います。

加えられる電圧信号が任意の場合、電流 I (t) は次のような２階の常微分方程式に支配されます。　定数 a, b, c はコイルやコンデンサーや抵抗によって決まります。　この形は、上で述べた陰形式の線形表現です。

以下の話をスムーズにするために、 とします。　こうしても、一般性を失いません。

そして、上の式を

のように書いて、電流 I (t) に線形操作 が作用すると考えましょう。　さらに、この作用を因数分解すると、

のように書けます。　 と は互いに複素共役な根です。　もちろん、実根の場合も含みます。　この形は、電流 I (t) に対して を作用させ、その結果に を作用させることを意味します。　まずは、１階の微分作用 による入出力関係を導きましょう。　システム内部にエネルギーの蓄積がない状態で、解をコンボリューションの形で求めます。

に、

を代入すると、次が得られます。

{　}内の最後のデルタ関数は、t=0 でいきなり非ゼロの電圧が印加された場合の単位衝撃を意味しています。t が微小時間 dt より以降 () では、｛　｝内がゼロから、このシステムのインパルス応答、

が得られます。　したがって、次の入出力関係を得ます。

なお、

なので、Ｚ が複素根のときは、まだ応答は複素信号です。　今度は、この を入力した場合、すなわち、

を求めれば、回路の入出力関係を得ることができます。　すなわち、

ここで、

なので、回路のインパルス応答は実信号になって、

のようになります。　回路が安定であるためには、 でなければなりません。　もし、Ｚ の虚部がゼロならば（実の重根ならば）、

なので、回路のインパルス応答は

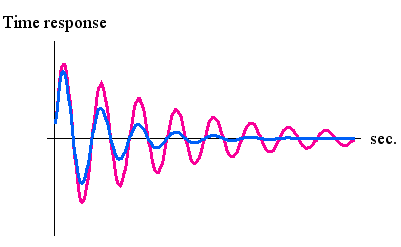
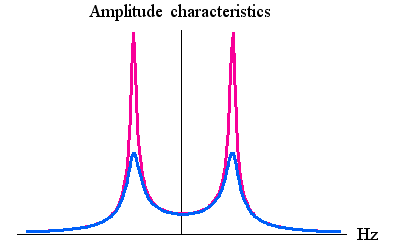
になります。

根の実部は時定数（インパルス応答の減衰の速さ）を、虚部は共振周波数を与えています。　下図に、共振周波数を固定して、時定数を変えたときの応答を示します。 赤いカーブは実部が小さい場合、青いカーブは実部が大きい場合です。

微分をラプラス変換のＳで表し、この有理関数で伝達関数が定義されます。　信号 V (t) がラプラス変換で与えられると、これに伝達関数を掛けた結果、

は出力電流のラプラス変換を与えます。　実際には、任意の信号をラプラス変換で表すのは困難ですが、典型的な信号に対してならば検討することが可能です。　微分作用Ｓの周波数特性は なので、これを上の伝達関数に代入すると、その周波数特性が得られます。　上図のインパルス応答に対応する周波数特性は下図のようになります。　このようにして、線形システムはインパルス応答または伝達関数または周波数特性で、完全に記述することができます。

注１：　上の例題では、インパルス応答 は負の時間で値をもちませんでした。　このことは、因果律  (Law of Causality) を満たしているといえます。　因果律は、「原因に先んじて結果がでることはない」ことを主張するものです。　しかし、画像処理などでは、横軸も縦軸も空間的ですから、因果律を満たすシステムではありません。　線形システムを扱うとき、因果律を満たす対象なのか、非因果的対象なのかを意識することは大切です。　時間の信号を扱う場合でも、因果律は微妙な問題を提起する場合があります。　たとえば、信号の微分や積分のような基本操作も、因果的なのか非因果的なのか疑問です。微分を参照してください。

注２：　高階の常微分方程式の入出力関係を求めるには、上の操作を機械的に繰り返せばいいのですが、実際には計算が大変です。　また、見通しの良い議論も、見通しの良い数値計算法も期待できません。　実際には、高階常微分方程式を、多次元の一階微分方程式

に変換して体系化します。