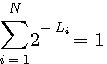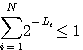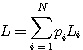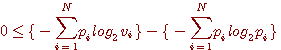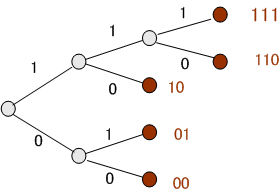
瞬時復号可能な符号語は、かならず下のように木グラフの先端に割り付けられなければなりません。

左端の根っ子に単位（＝１）の水量を仮定し、分岐するたびに水量を半分にして右へ流してゆきます。　すると、先端に流れ着いた水量は、その符号語の長さを とすると、 になります。　水量は分岐の途中で新たに注入されていないので、先端の水量の総和はちょうど１になるはずです。　

もちろん瞬時復号可能の中には、下図のように先端に符号を割り付けないものも考えられます。

このときは、符号が割り付けられた先端の総水量は１よりも小さくなります。　以上から、瞬時復号可能な符号に関して、一般に

が成り立ちます。　この不等式をクラフト（Kraft ）の不等式と呼んでいます。　逆に、符号長がクラフトの不等式を満たすような符号のセットは、必ず木グラスの先端に配置することができます。　一方、各符号語の生起確率を とすると、平均符号長は、

で与えられます。　ここで、次のような問題を考えてみましょう。

符号語の個数 が与えられた。
瞬時復号可能な（クラフトの不等式を満たす）符号化はたくさんあるが、
それぞれについて、符号語の生起確率を任意とする。
この条件下で、
平均符号長 の下限は？

直感的理解のために、簡単な例で上の問題を追ってみましょう。　まず、符号の数を４個とし、符号長を

としてみると、

なので、クラフトの不等式を満たしています。　先端のとり方によって、

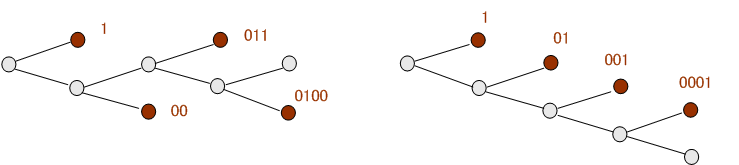
などが該当します。　しかし、一見して、このような符号は生起確率がどうであれ、無条件に平均符号長を小さくできます。　すなわち、左図の 0100 や、右図の 0001 は、下図のように直前の分岐点へ戻す方がベターですね。

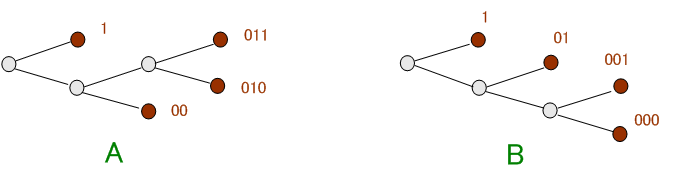
このグラフでは、すべての先端に符号が割つけられていることに注意してください。　そしてこのとき、クラフトの不等式は等式になっています。　他に、異なった構造をもつ木グラフとして下のようなものがあります。

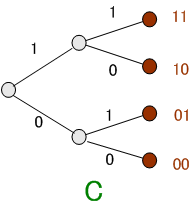
この例題では、４つの先端すべてに符号を割り付けるグラフはこの３つのタイプ （ Ａ と Ｂ と Ｃ ） だけです。　これ以外は、どれかと上下対称になっていて、構造的には同じです。　先端に溜まった水量をそれぞれ、 とすると、平均符号長は、

で表すことができます。　一方、エントロピーは

で与えられます。　先端のすべてに符号を割り付ける場合だけを考えてよかったので、

そして、もちろん、

が成り立っています。　以上から、この問題の回答として、次のことが期待できそうです。

条件（１）と（２）の下で、

Ｅ ≦ Ｌ

答えは”Yes” です（証明は、 を用いよ）。　これは「シャノンの補助定理」と呼ばれており、いろいろな定理の証明に役立っています。　以上の結論を言い換えると次のようにいうことができます。

無記憶情報源について、
瞬時復号可能ないかなる符号の平均符号長も、
その情報源のエントロピー以下にはならない

注１：　シャノンの補助定理は、任意の二つの確率分布の間に

が成り立っていることを示しています。　右辺は「Kullback-Leibler  の情報量 」 とも呼ばれており、二つの確率分布の違いを測る尺度としての意味をもちます。　

注２：　ここでは、具体的な理解のために、非瞬時復号可能な符号を作るストーリーを進めてきました。しかし、非常に長い２値系列を考えたとき、「復号可能」ということはそれらのテーブルを記憶して読み出す作業に過ぎません。　とすれば、非常に長い２値系列のサンプルを考え、その情報量と情報源のエントロピーの関係がどうなるかを確認すればいいわけです。　実際、情報源Ｓから発生される２値系列がエルゴード的であれば、その２値系列の情報量を長さで割った値が情報源Ｓの（１記号当たりの）エントロピーに近似することが証明されます（マクミラン（McMillan ）の定理）。