|
離散フーリエ変換 Discrete Fourier transform |
|
フーリェ (Fourier)変換
を、時間軸で離散化します。 時間きざみ幅を
となります。 次に、
のようになります。 ここで、記号の簡単のために、
とすると、
のような、すっきりした形になります。 これを一般に離散フーリエ変換と呼んでいます。 ただし、Mathematica
や MatLab のような数値計算ソフトに組み込まれている離散フーリエ変換は、次数が2のべきのき自動的にFFT(高速フーリエ変換)が適用されます。 その形式を導いておきましょう。 解析したい信号
次に、
これが高速フーリェ変換の前提となる形式で、いろんな数値計算ソフトで離散フーリエ変換として定義されているものです。 では、この形式で変換される
次に、変換行列を
を用いて書き直すと、
のようになります。 この変換行列をよく見ると、2行と8行、3行と7行、4行と6行、は互いに複素共役の関係にあります。 このことから、
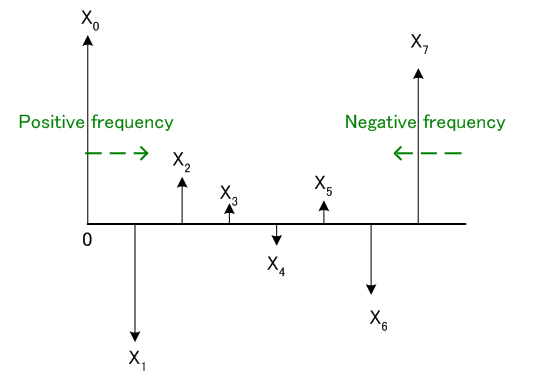
となっていることが分かります。 これは、正負両側の周波数成分を求めた冒頭の離散フーリエ変換の定義をぐるっと4つ分だけ巡回シフトした結果になっています。 図で表すと次のようになっています。 ここで、
注 :この変換行列は共役対称で、すべての行(または列)が互いに直交しています。 あるいは、この行列を
なる関係が成り立ちます。 ここで右肩の T は転置、*は複素共役を表します。 このような性質をもった行列をユニタリ行列 といいます。
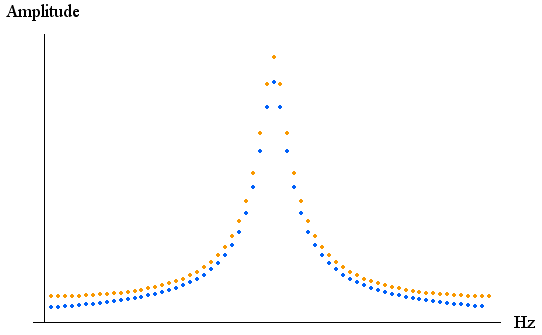
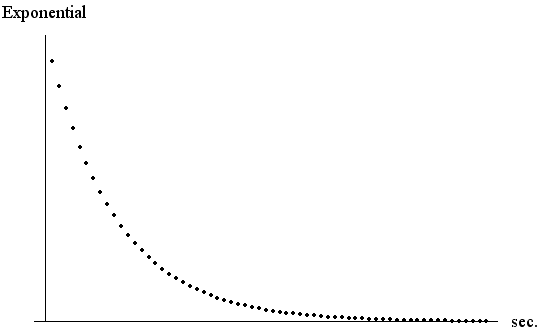
上のことは、大体の傾向です。 不連続点があって、滑らかに減衰するような信号の扱いは上の3.と4.の両方に当てはまってしまい、やっかいなケースの一つです。 たとえば、
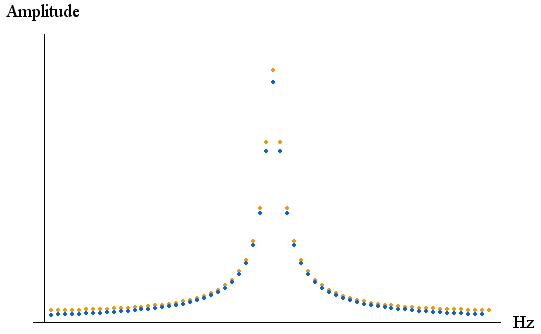
上の図で、離散フーリエ変換の結果が合っていないことがわかります。 時間幅をとりすぎましたね。 そこで、きざみ幅を半分にして64点をサンプルしてみましょう。 すると
のようになり、かなり真のカーブに近づいてきました。 大雑把にいえば、信号の打ち切りを見て、ぎりぎりまで時間幅を短くしたほうが良いということになります。 ただし、両方において、オレンジ色はいつも大きくなっています。 これは、t=0 での値を1 にしたことが影響しています。 その理由は、t=0 で値が定義されていないことから来ています。 現実的には、0 と1 の間の値をとるべきですが、この場合は0.7 ぐらいがベストです。 不連続点の一般的な扱いは困難ですが、両側から対称性をもって不連続点に接近するようなケースでは、中点を採用するとよいでしょう。 |
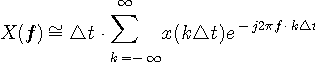
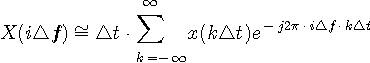
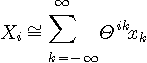
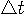 をどう選ぶかによってフーリエ変換の精度が左右されますが、精度の話は後回しにして、とりあえず定性的な話を進めます。
をどう選ぶかによってフーリエ変換の精度が左右されますが、精度の話は後回しにして、とりあえず定性的な話を進めます。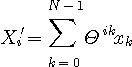
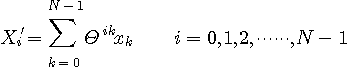
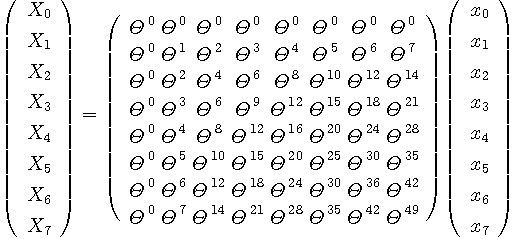
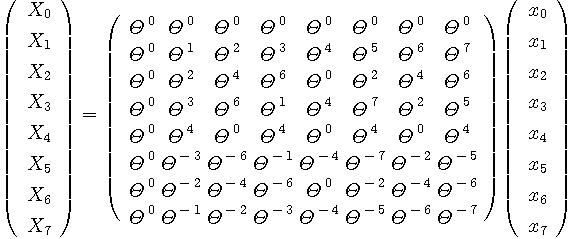
 で表すと。
で表すと。