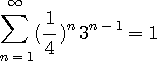|
フラクタル Fractal |
|
UWB (Ultra Wide Band) は約7GHzの帯域幅をもつインパルスを用い、このインパルスの間隔の大きさに情報を乗せて通信します。 「無線通信のゴミため = 無線LAN, Bluetooth, ZigBee, etc.がひしめく」と呼ばれる 2.4GHz のISMバンドの帯域幅が100MHzですから、7GHzはものすごく広い帯域ですね。 このインパルスを受信するアンテナはものすごく広帯域でなければなりません。 しかも、携帯端末に収まるように小型化する必要があります。 この目的のため、いろんなフラクタルアンテナが研究され、実用化されています。 たとえば、正三角形の金属板を用意し、その真ん中を正三角で打ち抜き、残った部分をまた正三角で打ち抜くという操作を繰り返したものです。 このようにすると、いろんな共振モードが得られ、どんどん広帯域化ができると期待されるわけです。
さて、現実的な問題から離れて、正三角の打ち抜きを、金属板がバラバラにならない限界の大きさで実行し、この操作を無限回繰り返してみます。 与えられた金属板の面積を1とすると、最初に打ち抜かれる一個の正三角の面積は
になってしまい、残った面積はゼロ、すなわち、実体のないアンテナになってしまいそうです。 下図は、打ち抜きをもう少し進めた図です。 無限に打ち抜いた結果をコンピューターのモニターで描画することはできませんし、計算量はたちまち爆発してしまいます。 下図から、極限を想像するしかありません。
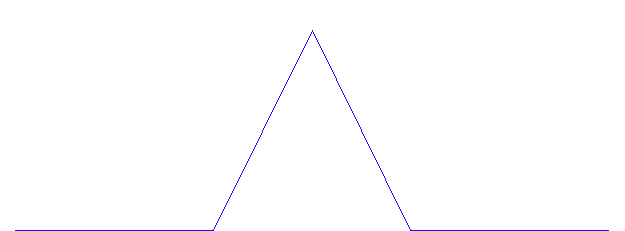
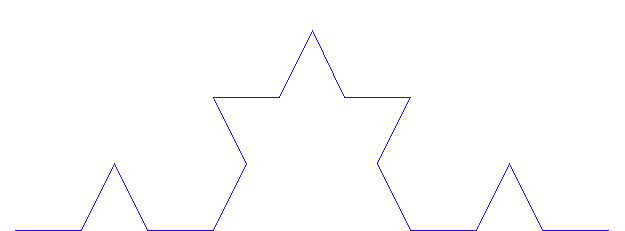
これは、シルピンスキー (Waclaw Sierpinskii, 1882-1969) のガスケットと呼ばれ、フラクタルの代表的なモデルです。 他に、フラクタルの代表的なモデルとして、コッホ曲線 (Niels Fabian Helge von Koch, 1870-1924) があります。 これは、次の操作を無限に繰り返したものです。
シルピンスキーもコッホも、 まず、変形された図形が与えられ、 という操作を無限に繰り返しました。 ということは、いくらズームインしても、その先には、無限に深い繰り込み図形が続いています。 ということは、微分や積分ができないということになります。 直感的にいえば、シルピンスキーのフラクタルは、葉脈標本のような細い網状のものを連想します。 一方、コッホのフラクタルは毛糸のような輪郭のない紐状のものを連想します。 実際、シルピンスキーは面から面積を打ち抜いて線へ、コッホは線に2次元的広がりを持たせて面へ、性質を変えようとしています。 通常、線や面や立体はそれぞれ、1個や2個や3個の座標軸で表現されます。 そして、線が線であるからには、面が面であるからには、立体が立体であるからには、その中の任意の点の「近く」は、それぞれ、線あるいは面あるいは立体で覆われていなければなりません。 常識的には、線上の点の「近く」には短い線分があり、「より近く」にはもっと短い線分があり・・・・・・、といった距離の極限が存在します。 しかし、コッホでは、どんなに短い有限区間をとってみても、そこに含まれる曲線の長さは無限になっています。 逆にシルピンスキーでは、どんなに狭い有限領域をとって眺めても、いたるところ面積が打ち抜かれています。 したがって、点へ連続的に接近するという概念や点の近くの幾何学的広さを測るといった概念が成り立たなくなります。 いままでの解析学はこれらの概念の上に立っていましたが、フラクタルには当てはめることがでません。 新しい「次元」が導入されなければなりません。 一般に、単純な操作でも、それを無限に繰り返すと、連続的な概念で扱えない世界に入っていきます。 カオスもそうですが、自然現象や社会現象の複雑さのモデルといえるでしょう。 注1: フラクタルには、確率を導入したものなど多くの定義があります。 また、自然界や生体や社会現象にもフラクタル的なものが存在します。 まずは、高安秀樹 「フラクタル」 朝倉書店 を読まれることを薦めます。 注2: コッホの曲線をトコトコとたどって行けば、その軌跡は実数軸へ写像されるはずだ(一次元だ)と考えることもできる。 トコトコとたどることは(Cantor が集合論で操作したように)、単なる実数への写像であって、次元という概念は別ものです。 概念(意味)は Peano, Cantor, Hilbert の線上にある形式主義からは一切生まれてはならないものであって、それに批判的であった直感主義者達、Poincare, Hausdorff, Brouwer によって次元の概念が確立された。 実は、コッホの次元は1.2618・・・、シルピンスキーの次元は1.585・・・と計算されています。 フラクタル次元の定義は非常に多く考えられていますが、規則的に生成された図形ならば、どの定義によっても同じ結果が得られなければなりません。 逆に、規則的でないものについては、定義によって結果が異なり、どの定義が妥当かという議論に引き込まれてしまいます。 コッホもシルピンスキーも平面上の図形なので、この平面を碁盤のように無限に分割していったとき、升目に図形が含まれるかどうかの割合を次元の概念に合致した式で評価するというのが、一般的な考えです。 非規則的なフラクタルでは、図形が含まれるかどうかを確率で表し、シャノンの情報量を導入する定義も考えられています。 |

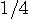 です。 次に打ち抜かれる3個の正三角の面積の和は
です。 次に打ち抜かれる3個の正三角の面積の和は 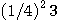 です。 次に打ち抜かれる9個の正三角の面積の和は
です。 次に打ち抜かれる9個の正三角の面積の和は 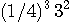 です。 これを無限に続けると、打ち抜かれる面積の総和は、
です。 これを無限に続けると、打ち抜かれる面積の総和は、