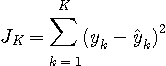|
ビタビ・アルゴリズム Viterbi algorithm |
|
既知のチャンネル歪みとAWGN (Additive White Gaussian Noise 加法的白色ガウス雑音)を仮定したとき、最良の受信方法は最尤(ユウ)系列推定でした。 その原理は次のようです。
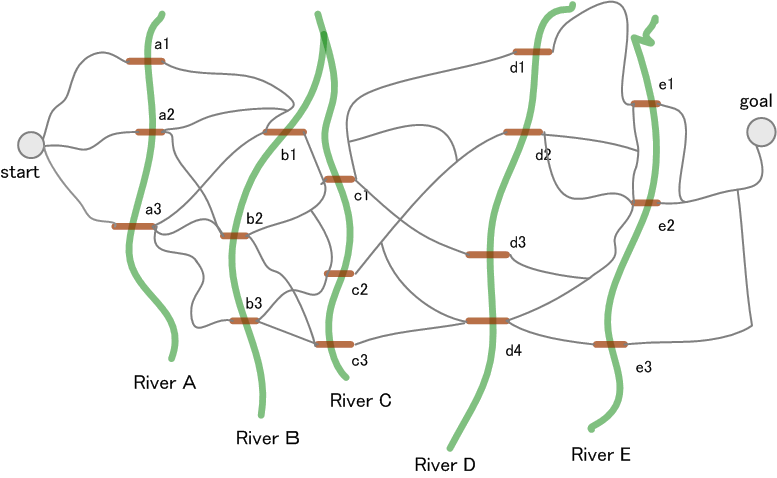
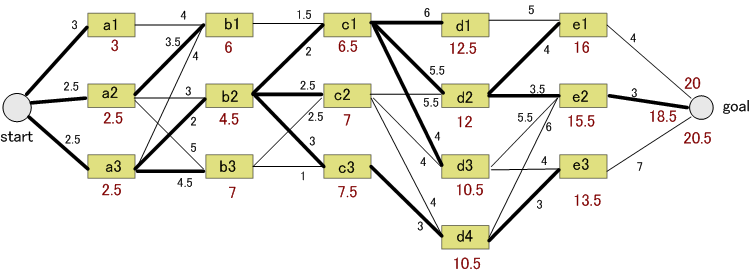
この手順は極めて単純ですが、シンボル系列が長くなると、演算量はあっという間に爆発してしまいます。 この演算量をシンボル長に比例するように工夫したのがビタビ (Viterbi) ・アルゴリズムです。 これは、Richard Bellman による DP: Dynamic Programming (動的計画法)をストレートに応用したものです。 というわけで、まず DP の例題を説明します。 下図のような5本の川が流れる地図があります。 スタートからゴールまでの最短ルートを求めなさい。
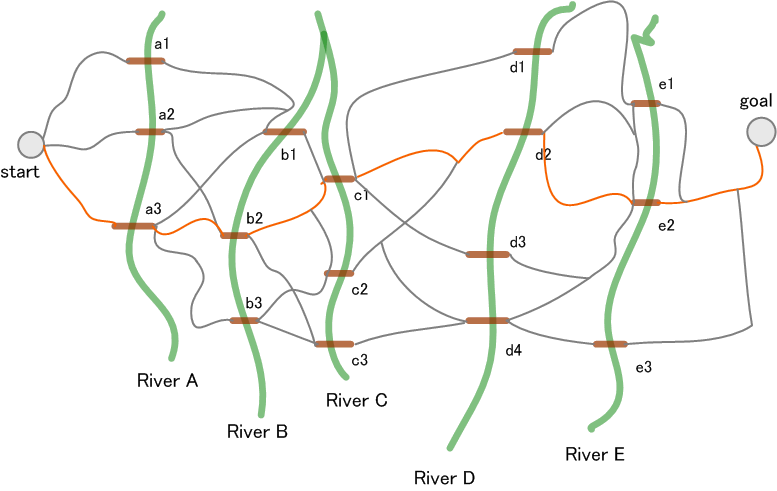
総当たり的に、ルートの距離を計算すると、ごちゃごちゃして嫌になりそうですね。 そこで、川に注目しましょう。 川には橋が掛けられていますが、橋までの最短距離を段階的に(川を段階と考えて)求めていきます。 とりあえず、橋から橋への最短ルートを地図から読み取り、それを下図のように整理してみます。
上の手順をまとめると、次のことが分かります。
特に、1.は、「現段階の最適戦略が、過去に遡ることなしに、直前の段階の最適結果だけから決まる」ことを意味しています。 このような原理を 「最適性の原理」 と呼んでいます。 DP はこの原理を前提にしていますが、その応用は非常に広い範囲にわたっています。 では、最尤系列推定 (MLSE: Maximum Likelihood Sequence
Estimation ) の簡単な例題を、DP の手順に書き直してみましょう。 既知のチャンネル応答を
受信機は、レプリカ
を次々と作って、永遠に続くであろう自乗誤差
を最小にしたい。 時刻KをK番目の川と見做し、この時刻のレプリカに含まれる送信シンボルの8通りの候補
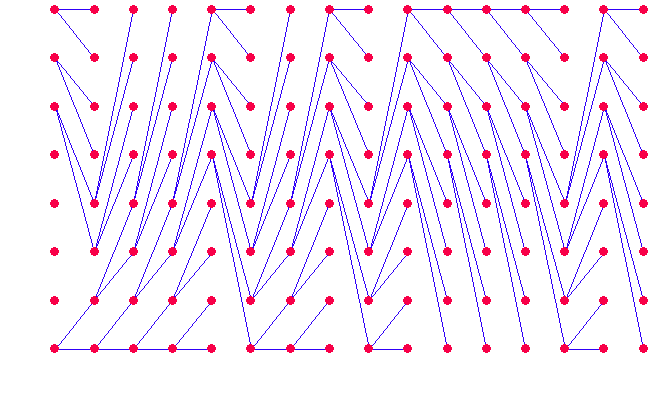
時刻Kの候補 {+1,+1,-1} からは、 時刻K+1の候補 {+1,+1,+1} と {-1,+1,+1} にしか行けません。 橋から出る道も入る道も2本に限定されます。 この様子を描くと下図のようになります。 赤い点は8個の候補を表し、左から右へ遷移します。 赤い点は下から上へ、 {-1,-1,-1,} {-1,-1,+1} {-1,+1,-1} {-1,+1,+1} {+1,-1,-1} {+1,-1,+1} {+1,+1,-1} {+1,+1,+1} に対応しています。 これをトレリスグラフ (trellis は植物を支えるフレーム構造)と呼んでいます。 この場合、赤い点に入る2本の道の距離はともに等しく、次の式で与えられます。
このグラフを冒頭の最短ルート問題に照らして考え、赤い点に入る短い方のルートを選択し、他の道をどんどん捨てると、生き残った道は下図のようになります。
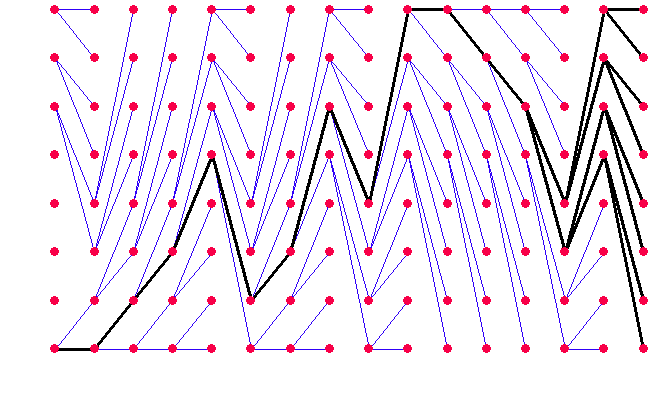
左端は時刻 K=1、右端は時刻 K=16に相当しています。 K=16のすべての赤い点から過去へ(左へ)遡ると、下図の黒いルートが浮かび上がります。
黒いルートは時刻K=13で合流(merge)しています。 そして、合流点より過去は一本のルートになっています。 したがって、時刻k=16でK=13以前の最短ルートが確定したことがいえます。 このシミュレーションの送信信号は {-1, -1, -1, -1, +1, -1, -1, +1, -1, +1, +1, +1, +1, -1, +1, +1, +1, -1} であり、正しく判定されていることが分かります。 合流を見つけて、確定したルートをどんどん延ばしていくことができるので、延々と受信が可能になります。 注: チャンネル応答が未知、送信シンボル系列も未知のとき、何の条件もなしに送信シンボルを推定できません。 これはブラインド問題になります。 ビタビ・アルゴリズムのブラインド版の解説はこのページにあります。 |
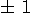 )とします。 ガウス雑音
)とします。 ガウス雑音